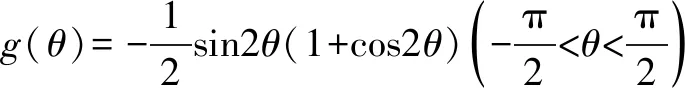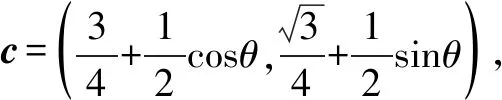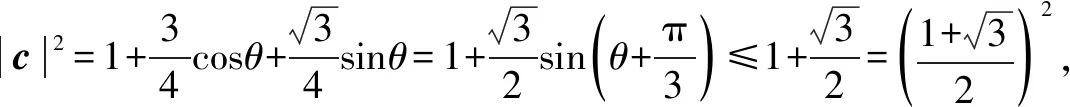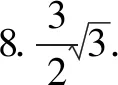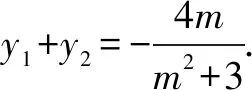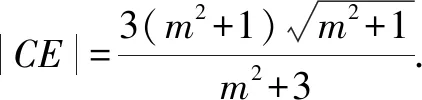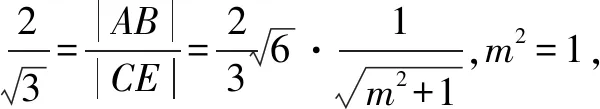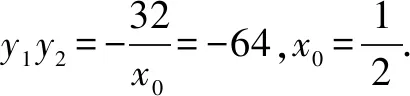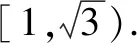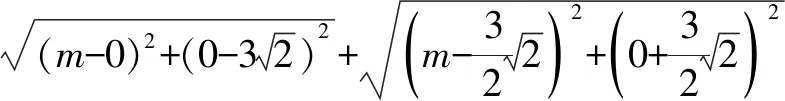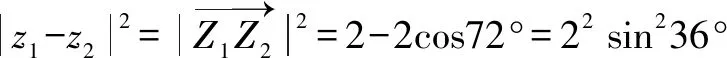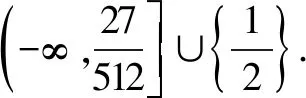2019年清华大学自主招生数学试题(部分)及其详解

2019-10-23甘志国

数理化解题研究 2019年28期

关键词：组数数学试题增函数

甘志国

(北京市丰台二中 100071)

2019年清华大学自主招生数学试题共包含35道不定项选择题.本文中的试题均是由参加考试的学生回忆得出的，因而回忆出的题目可能不准确(没有回忆出选项的题目均改成了填空题)，题目也不全，题号也不准确.解析由笔者给出.

1.若一个四面体的六条棱长分别是6,6,6,6,6,9，则其外接球的半径是____.

3.已知点A(0,2),B(0,-1)，若P是单位圆上的动点，则|AP|·|BP|2的最大值是.

4.若线段AB是⊙O的直径，CO⊥AB,M是线段AC的中点，CH⊥MB于H，则( ).

A.AM=2OHB.AH=2OH

C.△BOH∽△BMAD.AB=BM

5.已知集合A={1,2,3,…,15},B={1,2,3,4,5},f是A到B的映射.若f(x)=f(y)，则称有序数对(x,y)为“好对”.可得“好对”个数的最小值是.

C.f(x)=ex+1D.f(x)=sin(2x+1)

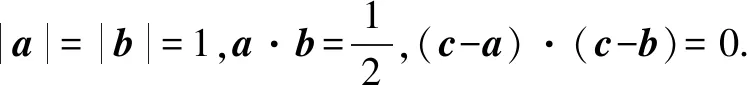
9.已知圆x2+y2=4，在该圆上的点(x0,y0)处的切线与抛物线y2=8x交于两点A,B.若∠AOB=90°(其中O是坐标原点)，则x0=.

10.若a=44444444,b是a的各位数字之和，c是b的各位数字之和，d是c的各位数字之和，则d=.

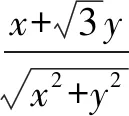
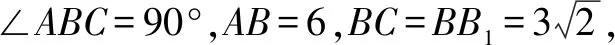
13.若数列{an}满足a1=3,an+1=an2-3an+4(n∈N*)，则( )

A.{an}单调递增 B.{an}无上界

14.若正数a,b满足ab(a+8b)=20，则a+3b的最小值是.

15.若f(x)=|x-1|+|x-3|,g(x)=2ex，则f(x)+g(x)的最小值是.

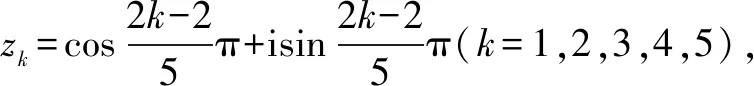
A.a1a3a4=125 B.a1a2a3a4a5=55

18.若实数x,y满足x3+8y3+6xy-1=0，则x3y的取值范围是.

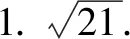
由分部积分公式，可得

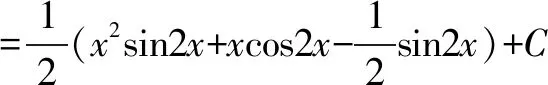
所以

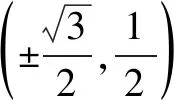
4.BC.

5.45.(1)当x=y时，“好对”(x,y)个数是15：x=y=1,2,3,…,15.

(2)当x

设B中的元素i的原像集是Mi，集合Mi的元素个数是xi(i=1,2,3,4,5)，可得x1+x2+x3+x4+x5=15(xi∈N,i=1,2,3,4,5).

可得xi(i=1,2,3,4,5)的最大值最少是3.

(3)当x>y时，同(2)可得“好对”(x,y)个数的最小值是15.

综上所述，可得所求答案是45.

6.AB.由拉格朗日中值定理可知，可导函数f(x)满足性质T即f(x)的值域是f′(x)的值域的子集.

(1)当f(x)=x3-3x2+3x时，可得f′(x)=3(x-1)2，因而f(x)的值域是R，f′(x)的值域是[0,+∞)，得选项A正确.

(3)当f(x)=ex+1时，可得f′(x)=f(x)，因而选项C错误.

(4)当f(x)=sin(2x+1)时，易知f(x)的值域是[-1,1].还可得f′(x)=2cos(2x+1)的值域是[-2,2]，因而选项D错误.

图3

10.7.可得a=44444444<(104)4444=1017776，因而a至多是17776位数，所以a的各位数字之和b≤17776·9=159984；因而b至多是6位数，所以b的各位数字之和c≤1+5·9=46；因而c至多是2位数，所以c的各位数字之和d≤3+9=12.

还可得a=44444444≡(4·4)4444≡74444=7·(73)1481=7·(38·9+1)1481≡7(mod9)

a≡b≡c≡d(mod9),所以d=7.

图4 图5

13.ABD.由题设，可得a1=3,an+1-an=(an-2)2≥0,an+1≥an(n∈N*)，再由数学归纳法可得an≥3(n∈N*).进而可得an+1-an=(an-2)2≥(3-2)2=1,an+1≥an+1(n∈N*)，所以选项A,B均正确，C错误.

进而可得当且仅当(a,b)=(2,1)时，(a+3b)min=5.

15.6.设h(x)=f(x)+g(x)，可得

当x≤1时，可得h(x)=2ex-2x+4,h′(x)=2(ex-1)(x≤1)，进而可得h(x)在(-∞,0),(0,1)上分别是减函数、增函数，所以h(x)min=h(0)=6；当1≤x≤3时，可得h(x)=2ex+2是增函数，所以h(x)min=h(1)=2e+2>6；当x≥3时，可得h(x)=2ex+2x-4是增函数，所以h(x)min=h(3)>6.综上所述，可得答案.

当3x-100<3y-100时，可得3x-100是24·54的小于100的正约数即1,2,4,8,16,5,10,20 40,80,25,50.但3x-100是被3除余2的正整数，所以3x-100=2,8,5,20,80,或50，此时可得解的组数是6.

同理可得，当3x-100>3y-100时解的组数也是6.

综上所述，可得答案是12.

17.ABCD.可得zk(k=1,2,3,4,5)是方程z5=1的全部复数根，在复平面上对应的点是单位圆的内接正五边形的顶点Zk(k=1,2,3,4,5)，其中z1对应的顶点是Z1(1,0).

由对称性，可得a1=a2=a3=a4=a5,

①