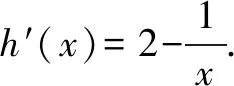有效破解导函数零点不可求的四个策略

郭明龙

(江苏省南京市高淳高级中学 211300)

一、本就无根，重组破之

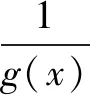
评注此类导函数零点不可求问题的典型特征是导函数看上去比较复杂，类型相对不清晰.

处理该类问题首先可以通过直接观察发现导函数是否恒正或恒负，若不能再尝试将导数进行适当的恒等处理，一般是提取公因式之后把导函数拆成两个子函数之差，分别求出两个子函数的最值或是通过适当的放缩之后明确各子函数取值的上下限，然后通过作差判别出导函数的正负.当然，该类问题也可以通过多次求导实现导函数正负的间接判断.

二、投石问路，先猜后证

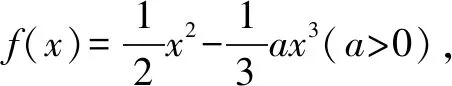
(1)求函数f(x)的极值；

(2)若a=e，

(ⅰ)求函数g(x)的单调区间；

(ⅱ)求证：x>0时，不等式g′(x)≥1+lnx恒成立.

解(1)及(2.ⅱ)略.

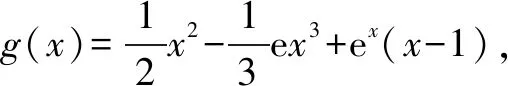
评注该类问题的一个显著特征是导函数一般是个超越函数，且其一个根x0很容易看出来，但是除了这个易得的根x0导函数还有没有其他根却暂时无法判别.遇到这种问题我们一般可以用多项式除法把导数先进行因式分解，即有f′(x)=(x-x0)g(x)，接下来我们或是直接看出g(x)根的情况，或是利用导数继续研究g(x)，研究单调区间以及极值最值等性质，进而搞清楚原导函数的根的情况.

三、设而不求，韦达相助

例3 (2017江苏高考)已知函数f(x)=x3+ax2+bx+1(a>0,b∈R)有极值，且导函数f′(x)的极值点是f(x)的零点.(极值点是指函数取极值时对应的自变量的值)

(1)求b关于a的函数关系式，并写出定义域；

(2)证明：b2>3a;

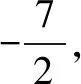
(2)略.

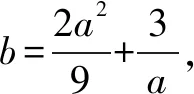
评注这类问题的最显著特征就是导函数是一个存在实根的二次函数，但是虽然导函数有实根，但是这个根却是绝对“不能”求的根.遇到这类问题，我们一般需要分析目标函数，看看是否可以通过借鉴解析几何中的技巧，设而不求利用韦达定理实现避免直接求导函数零点.这种独特的二次函数零点处理方式的应用还是特别广泛的，在平时的教学中老师应该加强这方面的引导，学生也应注意这种技巧的使用.

四、锁定区间，以虚代实

例4 (2017全国卷(2))已知函数f(x)=ax2-ax-xlnx，且f(x)≥0.(1)求a；(2)证明：f(x)存在唯一极大值点x0，且e-2

解(1)a=1(过程略).

评注这类问题的本质是导函数零点在定义域内存在但无法通过正常手段求出来，这应该是我们最不想遇到的情况，无法求出零点就意味着无法透彻研究原函数.这种问题往往需要借助于导函数的单调性及零点存在定理，以此确定这个无法求出的零点所在的相对比较小的区间范围，同时一定要注意体现该零点地位的式子即使得导函数等于零，如上题中的lnx0=2(x0-1).这样当有了导函数零点所在的区间以及体现此零点为极值点的式子，我们就可以近似地认为导函数的零点被“求出来”了.

导函数零点不可求实为命题者刻意为之，主要就是为了考查学生对于高中函数零点问题的一些常见处理策略是否能够掌握到位.这就要求我们老师在平时的教学中能够经常灌输这些常见的小技巧、小策略.以期能够让学生达到“宏观求聚敛，微观求发散的目的”.同时我们学生需要多找一些此类型题目做做，其实难题就那几种类型，做多了，熟练了这些解题策略就会内化成个人的一种能力素养.本文仅仅就一些常见的导函数零点不可求问题做了点简单的探究，在这块问题上还有许多问题值得日后继续研究.