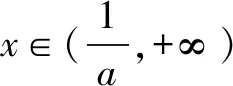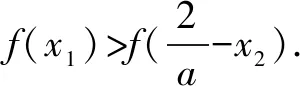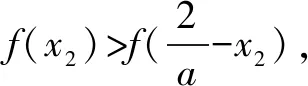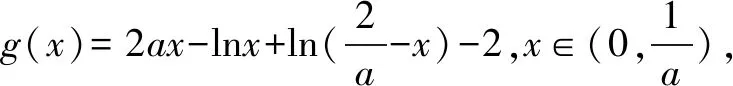与函数零点有关的证明问题解决之我见

徐敏亚

(江苏省梅村高级中学 214112)

2018年9月10号，全国教育大会在北京召开.这次大会主要研究培养什么人，怎样培养人，为谁培养人这一根本问题，而高中数学核心素养的颁布指明了在数学学科方面通过高中教育我们培养的学生具有什么样的核心素养以及怎样培养数学素养这两个问题，它是全国教育大会精神在数学学科方面的具体体现.高中数学核心素养包括：数学抽象，逻辑推理，数学建模，直观想象，数学运算和数学分析这六个方面，其中数学抽象放在了第一位，可见其重要性.数学抽象是指舍去事物的一切物理属性，得到数学研究对象的思维过程，它贯穿于高中教育阶段数学教育的全过程，甚至可以延续到大学、研究生阶段的数学教育，而教会学生掌握并使用这个核心素养去解决问题正是培养什么人的关键.

众所周知，与函数零点有关的证明问题在近几年的高考和各种模考中作为热点以压轴题的形式给出，很多学生对待此类问题往往是束手无策，而且此类问题变化多样，有些题型是不含参数的，但更多的题型又是含有参数的.此类问题处理的手段有很多，方法也有很多，但其实最常见的处理方法就两种，下面我们通过两个例题一一来探索.

一、消去参数，构造新函数，利用新函数的单调性解决问题

设x1,x2是函数y=f(x)的两个零点，且x1

证明∵x1,x2是y=f(x)的两个零点,

要证x1x2-x2

∵x10,

∴g(t)在t∈(1,+∞)上单调递增.

∴g(t)>g(1)=ln1+1-1=0,

又设h(t)=lnt-t+1(t>1)即证h(t)<0.

∴h(t)在t∈(1,+∞)上单调递减.

∴h(t)

即lnt-t+1<0,得证.

综上：x1x2-x2

招式分析函数零点的证明问题其实就是导数的应用问题，呈现的形式往往非常简洁，涉及函数的双零点和一个参数，是一个多元的数学问题，我们面对这类问题很自然地就会想方设法消去参数，从而使得多元问题变为双元问题.不管待证的是两个变量的不等式还是导函数值的不等式，解决的策略都是把双变量的问题转化为一元变量的问题求解，而途径就是通过换元构造一个新的一元函数，利用新函数的单调性解决问题.

二、保留参数，构造新函数，利用原函数和新函数的两次单调性解决问题

例2设函数f(x)=ax-lnx-1(a>0).

证明∵f(x)=ax-lnx-1，

∵a>0,x>0,

又∵f(x1)=f(x2)=0,且x1>x2,

又f(x1)=f(x2),

招式分析此类问题也称之为极值点的偏移问题，由于思 路固定，所以通常情况下求导比较复杂，计算时需细心.解决口诀：极值偏离“对称轴”，构造函数觅行踪；四个步骤环相扣，两次单调随其后.

总之，在高考创新试题层出不穷的大环境下，学生首先要掌握基本的知识方法和解题策略，就是我们一直强调的通性通法，对新题、难题的突破，就是需要在掌握好双基的前提下用数学能力提炼抽象出问题的本质，淡化特殊技巧，重视通性通法，去模式化的解题策略，以不变应万变，培养学生分析问题、解决问题的能力.只有学生学会自我分析，用数学抽象的核心素养把问题转化为熟悉的问题，从而用熟知的知识方法去解决未知的创新试题，这样才能真正培养学生的能力，才是数学核心素养在高中数学教育的真正体现.