一种基于图像邻域灰度变化的角点检测改进方法

杨佳豪,董静静,袁 彤,何雨恒,杨 丹,石美红

(西安工程大学 计算机科学学院,陕西 西安 710600)

0 引 言

角点包含图像中的重要结构信息,且信息的数据量少,是数字图像范畴中极为重要的特征点。因其具有旋转不变性、尺度不变性,同时对光照变化、仿射及投影变换也有一定不变性等特点[1-4],在相机标定[5]、图像拼接[6]、三维建模[7]、目标跟踪[8]等机器视觉领域有很高的应用价值。

角点检测方法可分为基于边缘轮廓、基于模型和基于灰度变化3类角点检测[9].基于边缘轮廓的角点检测严重依赖图像的边缘检测性能,一旦图像边缘出现中断,直接影响角点提取的质量。基于模型的角点检测是采用定义的模板,以待测像素为中心,通过比较周围像素和中心像素的灰度强度来寻找角点,诸如经典的SUSAN算法[10]，其优点是对噪声不敏感,但边缘点和角点区分不明显,运算速度比较慢。为此,邵泽明等[11]提出了一种基于SUSAN算法的分层快速角点检测算法,可较大幅度地提高运算速度,节省运算时间;文献[12]提出了一种基于灰色绝对关联度分析的角点检测算法,该算法的综合检测性能较好,且算法简单、易于实现;陈洪等[13]通过改进SUSAN算法中灰度差阈值的获取方法,提出一种自适应的角点特征提取方法,提高了角点检测的精度,缩短了角点特征提取时间,具有较好的鲁棒性。基于灰度变化的角点检测是根据图像像素点的灰度值变化提取角点,诸如经典的Harris算法[14]，其优点是计算量小、鲁棒性好,但角点检测的性能依赖于所选取的高斯窗口大小和阈值,且易受到噪声影响。针对Harris算法存在的缺陷,文献[15]提出了一种基于变分B样条滤波与快速局部窗口搜索相结合的Harris特征点检测算法,角点检测定位准确、抑噪性好;文献[16]提出了一种快速预筛选方法,并结合多阈值角点提取及邻近角点剔除策略,有效避免了角点簇拥现象,提高了角点检测效率;文献[17]通过在Harris算法中采用一种加权系数滤波窗口,有效地降低了噪点对角点检测的干扰,提高了角点检测的精准度。基于Harris和SUSAN 2种算法的优势互补,文献[18]提出了一种 Harris 邻域像素取差法与SUSAN相结合的改进算法,改善了角点检测的准确性;文献[19]提出了一种基于灰度差分与模板的Harris角点检测快速算法,能准确地提取图像中的角点,并去除了大量的伪角点。

受文献[19]的启示,文中提出了一种基于图像邻域灰度变化的角点检测改进方法。根据常见的X型、T型和Y型3类角点的空间分布特点，借鉴Harris角点检测算法思想,对图像进行第1次角点集筛选,然后基于USAN模板内的分布离散度对初始角点集进行第2次角点集筛选,最后采用非极大值抑制函数,从第二次筛选的角点集中提取角点。将本文改进方法分别与 Harris 算法、SUSAN算法和文献[19]算法的角点检测结果进行对比,说明了文中改进方法的有效性。

1 经典角点检测算法

Harris算法[14]是基于窗口的图像灰度变化自相关性来检测角点。在图像上无论怎样滑动窗口,如果图像的灰度值均变化较大,则认为窗口区域存在角点。窗口误差函数计算式为

(1)

对I(x+u,y+v)进行二元泰勒级数展开得到

(2)

式中:I(x,y)和I(x+u,y+v)分别表示位于(x,y)和(x+u,y+v)的像素灰度值;w(x,y)为高斯函数;Ix表示在x方向的偏导数;Iy表示像素在y方向上的偏导数。令

设M的特征值是λ1和λ2,分别反映了x方向和y方向的极值曲率。当这2个正交方向上的极值曲率均较大时,疑似为角点。位于(x,y)像素的角点响应函数为

CRF(x,y)=detM-k(traceM)2

(3)

式中:detM=λ1λ2;traceM=λ1+λ2;k是经验值,通常取0.04～0.06。如果CRF(x,y)的值大于预先设定的阈值T,那么位于(x,y)像素的疑似角点才为真正角点[19]。由于Harris算法是利用图像一阶或二阶偏导数来检测角点,若不存在大尺度变化,提取的角点稳定可靠,但对噪声敏感,对于T型角点的定位精度低[20]。

SUSAN算法选用由37个像素点组成的环形窗口模板(如图1所示)检测角点。

图 1 7×7环形窗口模板

其中心为被检测点,也称为核心点。根据模板内被检测点的周围邻域像素灰度强度与核心点像素灰度强度差的不同,被划分强度不相似区域和强度相似区域(即核值相似区USAN),其计算模型为

(4)

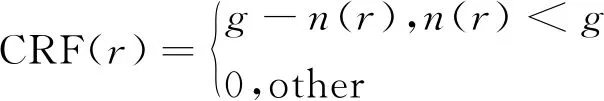
(5)

式中:I(r)表示周围邻域像素r的灰度强度值;I(r0)表示核心像元r0的灰度强度值;t为相似度阈值;CRF(r)为角点检测值,非零为疑似角点;n(r)=∑f(r)为f(r)的累加和,表示USAN面积;g为角点响应几何阈值,取环形窗口模板面积的1/2[10]。然后,利用USAN的重心远离圆形模板核心位置来去除伪角点。由于SUSAN算法是利用USAN的面积大小来检测角点,所以抗噪能力强、角点检测效率高,但是因没有考虑USAN的形状分布,致使角点的定位准确性较低,难以区分诸如X型角点与边缘点。

2 改进的角点检测方法

2.1 算法思想

在图像中,角点往往位于两直线的交点,即至少有2个或2个以上灰度变化较明显的区域相交的汇聚点。因此,角点至少在2个方向上都有较大的灰度变化。常见角点有X型、T型、Y型。图2是基于7×7窗口的不同角点分布的部分示意图,其中,USAN面积的相似区域面积均为18。

(a) X型角点 (b) T型角点

(c) Y型角点 (d) 边缘图 2 基于7×7窗口的不同角点分布示意图Fig.2 Diagram of distribution of different corner based on 7×7 window

首先,利用像素灰度变化的空间自相关和角点的形状分布特征,基于3×3邻域环形模板,依次扫描图像,进行第一次角点初筛,得到初始角点集,再根据USAN分布的离散度,对初始角点集进行第2次角点定位,得到准角点集,然后,采用非极大值抑制法,从准角点集中得到最终角点集。

2.2 基于灰度变化的空间自相关的角点初筛

为了降低遍历检测角点的时间开销,选用一个3×3邻域环形模板(如图3所示)。

图 3 3×3环形窗口模板

对像素进行初始角点筛选。首先,计算中心像素c与周围相邻像素的灰度差值

σ(i)=|I(i)-I(c)|

(6)

式中:i=0,1,2,…,7;I(c)和I(i)分别表示位于(c)和(i)的像素灰度值。然后,利用图像灰度变化的空间自相关性,分别计算沿中心像素c的x方向I(3)、I(7)，y方向I(1)、I(5),45°方向I(2)、I(6)和135°方向I(0)、I(4)与中心像素I(c)的灰度差值σ(i),按式(7),判断其是否均小于等于阈值T(阈值T根据经验值设置)。

(7)

如果是或者仅在一个方向上存在大于T,则移动窗口进行下一像素检测。否则,统计周围相邻像素与中心像素的灰度相似的数目个数

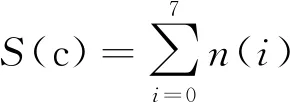
(8)

根据角点的形状特征和模板中相邻像素与中心像素的灰度相似度分布(图4是部分灰度相似度分布图),初筛角点如下:当S(c)值在[0，1]范围时,表明中心像素的灰度与邻域像素的灰度不相似,则中心像素为噪声点;当S(c)值在[7，8]范围时,表明中心像素的灰度与邻域像素的灰度相似,则中心像素位于平坦区;若S(c)值在[2，3]范围时,直接将中心像素标记为准角点;当S(c)值在[4,6]范围时,再进行第2次角点筛选。

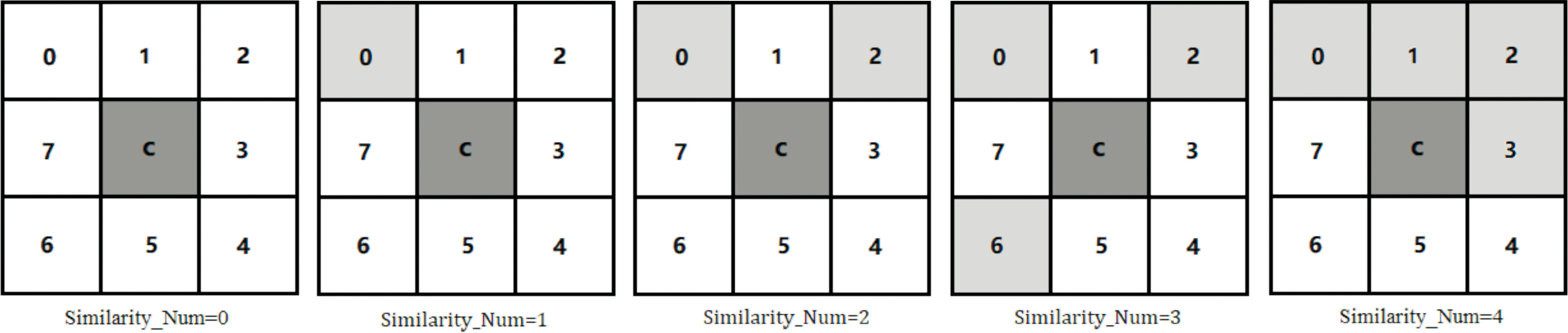
图 4 与中心像素灰度相似的邻域像素灰度分布示意图Fig.4 Diagram of distribution of neighborhood pixel gray level similar to central pixel gray level

2.3 基于USAN分布离散度的角点二次定位

从图2可看出,若为角点,其围绕中心像素点的邻域像素点的相似区域分布是离散的,否则，其相似区域分布是连续的。针对X型、T型、Y型3类角点,对值在[4,6]范围的初筛角点进行二次定位。

首先,采用式(4)和(5),计算USAN面积。如果USAN面积值大于g时,则从初筛角点集中剔除。如果USAN面积值小于g时,则定位为准角点,否则,选用图2的3×3邻域环形模板,依次对从编号0到7的8邻域像素,判断其相似区域的空间分布,若相似区域空间分布的离散度大于2,即由n(i)到n(i+1)的值由1跳变为0或者由0跳变为1的次数之和大于2,其中,i=0,1,2,…,7,i+1=(i+1)mod 8,则可定位为准角点,否则,从初始角点集中剔除。例如,图2(a)的X型角点的8邻域相似区域分布离散度为3;图2(b)的T型角点的8邻域的相似区域分布离散度为4;图2(c)的Y型角点的8邻域的相似区域分布离散度为5;而图2(d)位于边缘的中心像素,其8邻域的相似区域分布离散度小于等于2。

2.4 基于局部非极大值抑制的角点精准定位

首先计算待测准角点在x，y，xy方向的灰度变化梯度值,然后根据其角点响应值,采用局部非极大抑制法,精准定位角点。具体步骤如下:

第1步 采用3×3窗口的Sx(i)和Sy(i)(如式(9)所示)模板,以准角点i为中心,分别计算它与邻域像素在x和y方向上的灰度变化梯度;

(9)

第2步 根据x和y方向的灰度变化梯度,计算准角点i在x，y，xy方向的梯度值,即

τx(i)=Sx(i)2,τy(i)=Sy(i)2
τxy(i)=Sx(i)Sy(i)

(10)

第3步 计算准角点及其邻域像素的响应值

R(i)=τx(i)×τy(i)-τxy(i)2-t×

(τx(i)+τy(i))2

(11)

其中t∈[0.04,0.06]。

第4步 在3×3窗口内,若Ri为局部极大值,则定位为角点,否则,从准角点集中剔除。

图5是利用改进算法对三角形图进行角点检测的实验结果图。

图 5 改进算法的实验结果图Fig.5 Experimental result diagram of improved algorithm

3 实验结果与分析

改进算法在处理器为Inter(R) Core i5-7300HQ 2.50 GHz、内存8 GB的计算机上运行。实验数据分别采用模拟几何图像和真实图像进行实验,并与Harris算法、SUSAN算法和文献[19]算法进行对比。

为了客观评价角点检测算法的性能,选择常用的一致性(CCN，Consistency of Corner Numbers) 和准确性(ACU，Accuracy)评判准则[21]进行性能评价,其计算式为

CCN=100%×1.1-|Nt-No|,

(12)

式中:No表示检测到原图像的角点数;Nt表示加噪后检测到图像的角点数;Ng表示原图像的真实角点数;Na表示与真实角点相匹配的实际检测到的角点数。

图6和表1为对2种模拟几何图像进行角点检测的实验结果。

(a) 模拟几何图像1

(b) 模拟几何图像2图 6 不同角点检测算法对模拟几何图像的检测结果

图像算法检测角点数正确角点数伪角点数漏检角点数ACU/% 模拟几何图像1Harris算法943856465.45 SUSAN算法573918380.64 文献[19]算法44422097.72 本文算法424200100模拟几何图像2Harris算法753144169.10 SUSAN算法503119179.44 文献[19]算法33321098.48 本文算法323200100

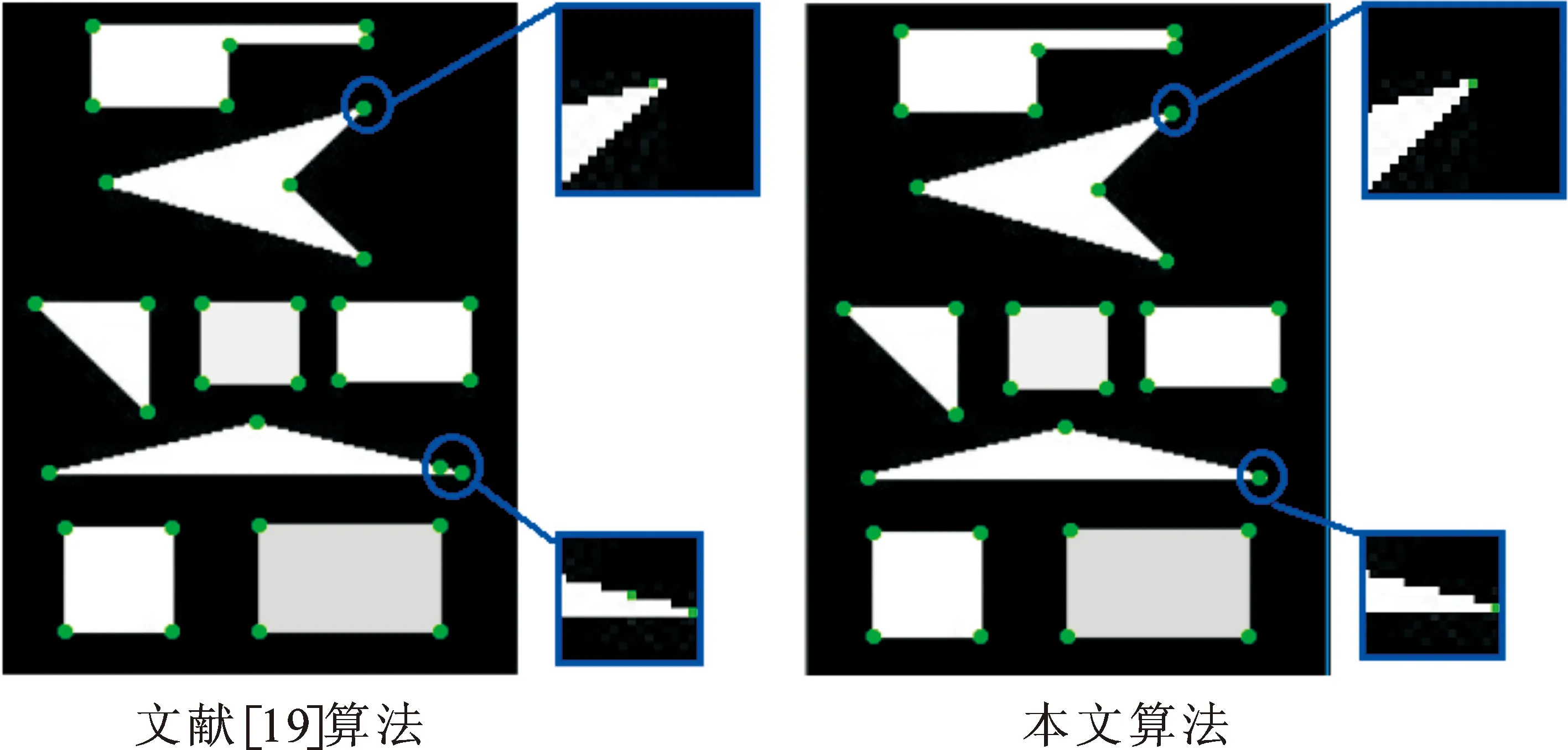
从图6可看出,Harris算法存在角点簇和角点漏检的现象;SUSAN算法有所改进,但存在部分伪角点;从放大图中可看到,文献[19]算法也存在少量的角点簇,相对其他算法,本文改进算法能检测到真实角点。从表1可以看出，依据客观评价指标, Harris算法因存在大量的角点簇和少量的漏检角点,致使ACU分别为65.45%和69.10%;相对Harris算法和SUSAN算法的角点检测准确性能有所改善,ACU分别为80.64%和79.44%;文献[19]算法进一步改善了角点检测准确性能,ACU分别为97.72%和98.48%。相比而言,本文改进算法很好地剔除了伪角点,角点检测准确性能均达100%。

图7和表2是对用于相机标定的棋盘图进行角点检测的实验结果。从图7可以明显看到,Harris算法存在角点簇,SUSAN算法有漏检角点或角点定位偏离;文献[19]算法能检测到棋盘格中全部角点,但仍存在少量伪角点或角点定位有点偏差;相对文献[19]算法,本文改进算法能精准定位棋盘格的全部角点,ACU提升了4.26%。

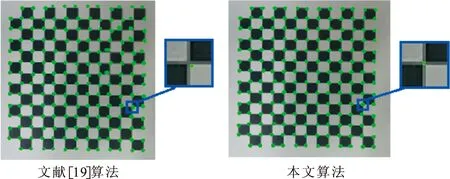
图 7 不同角点检测算法对棋盘格图的检测结果Fig.7 Detection results of different corner detection algorithms on checkerboard images

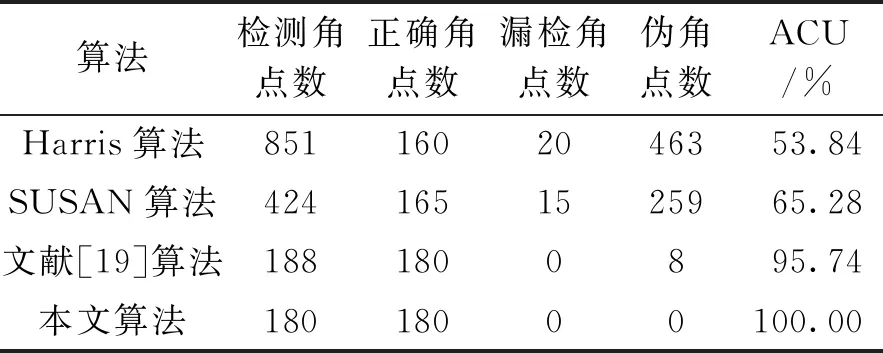
算法检测角点数正确角点数漏检角点数伪角点数ACU/% Harris算法8511602046353.84 SUSAN算法4241651525965.28 文献[19]算法1881800895.74 本文算法18018000100.00

为了进一步验证本文改进算法的有效性,选用真实图像进行实验验证。图8和表3为部分真实图像的角点检测结果。可以看出,所有算法都存在漏检角点(见红色标记)和伪角点问题,但是,Harris算法和SUSAN算法存在着明显的角点簇,诸如房檐。文献[19]算法和本文改进算法有了较大改善,本文改进算法的角点定位更精确(见放大图)。

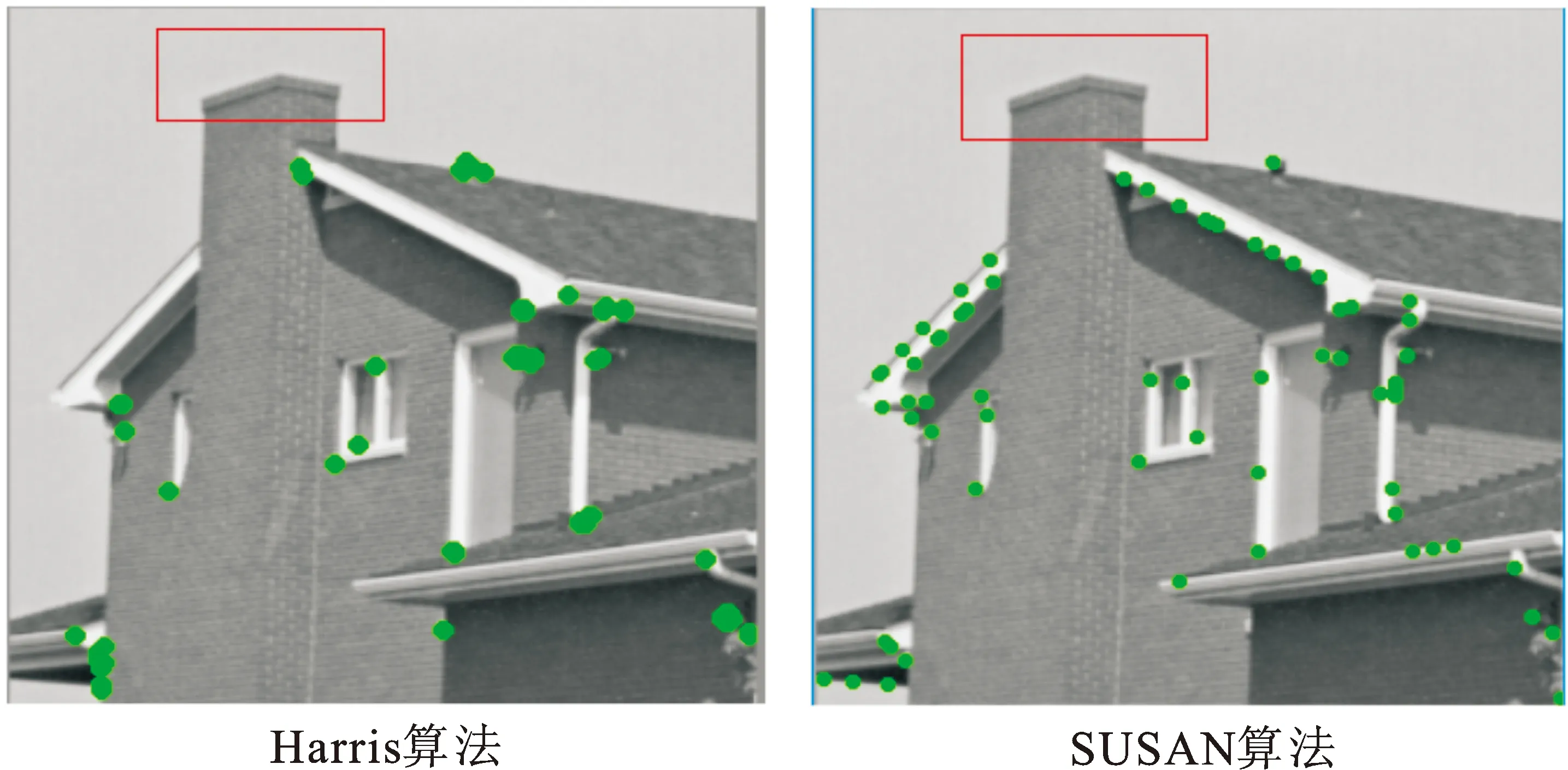
(a) 真实图像1

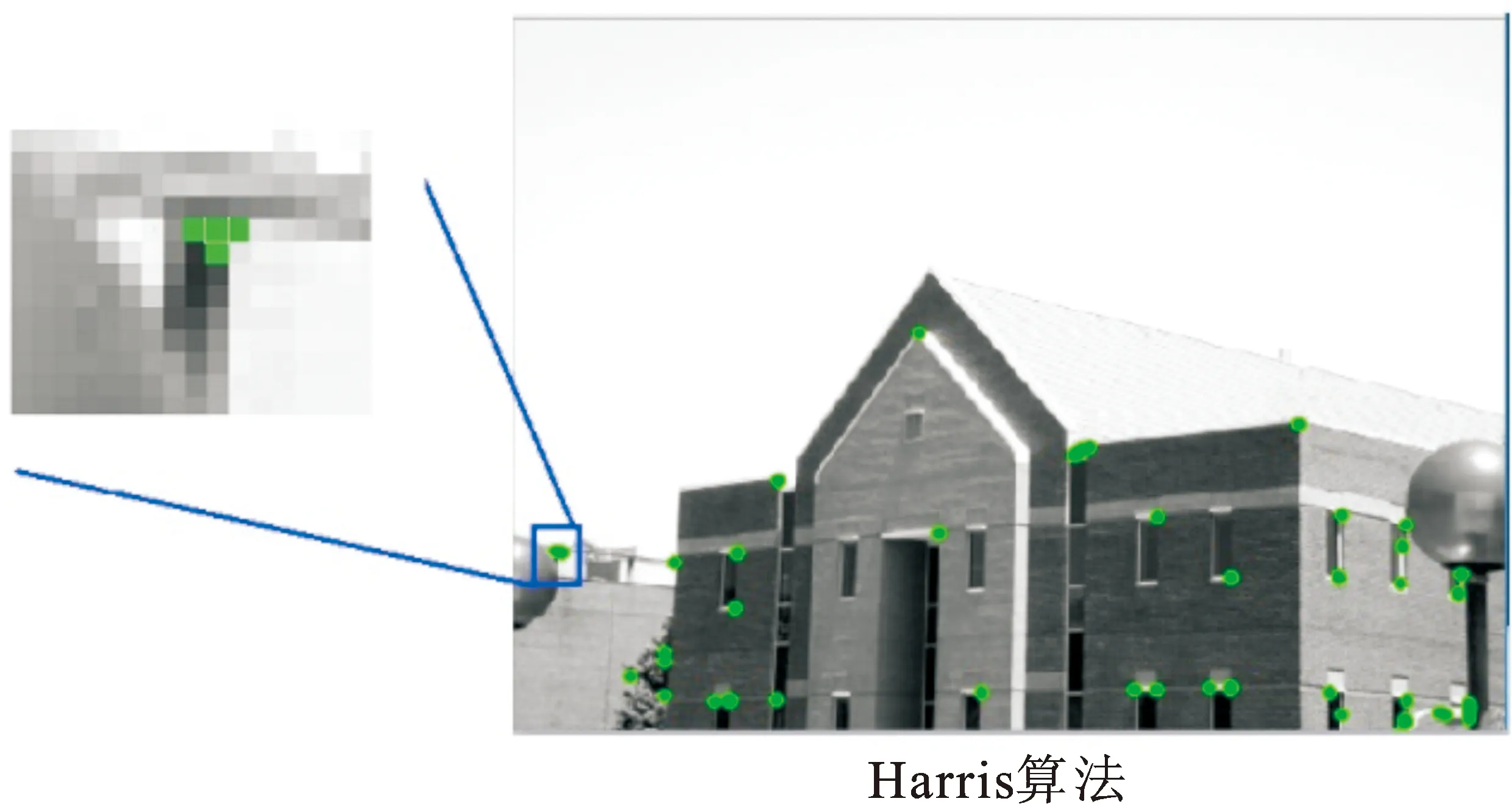
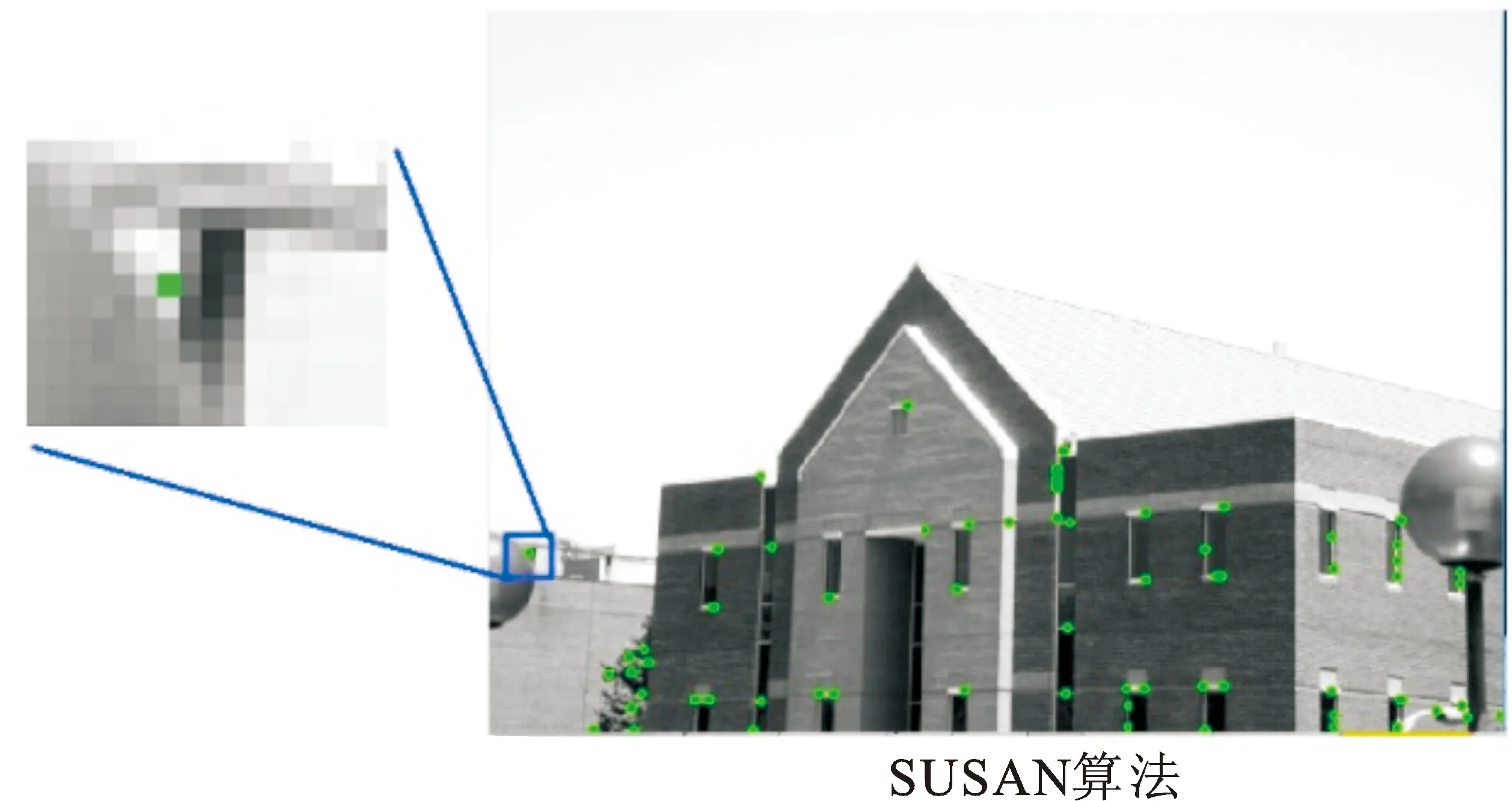
(b) 真实图像2

图8不同角点检测算法对真实图像的检测结果

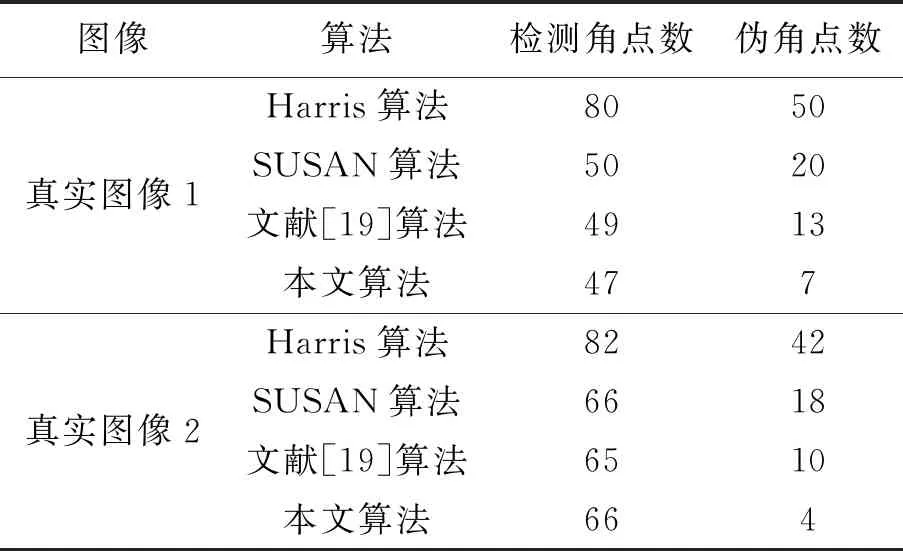
Fig.8 Detection results of different corner deterction algorithms on real images

为了测试本文改进算法的抗噪性,对图6(b)的模拟几何图像和图8(b)的真实图像分别加入不同密度的椒盐噪声和不同方差的高斯噪声,对比其一致性指标CCN,结果如图9所示。随着噪声密度的增加,各算法的CCN下降,Harris算法最明显,其次是SUSAN算法,文献[19]算法和本文改进算法的CCN性能明显好于Harris算法和SUSAN算法。但是,随着椒盐和高斯的噪声密度加大,本文改进算法的CCN性能优于文献[19]算法。对于模拟几何图像,当高斯噪声的方差值大于0.6时,文献[19]算法的CCN值低于本文改进算法;对于真实图像,当高斯噪声的方差值大于0.4时,文献[19]算法的CCN值下降速度明显比本文改进算法快。

(a) 模拟几何图像抗椒盐噪声的CCN变化曲线

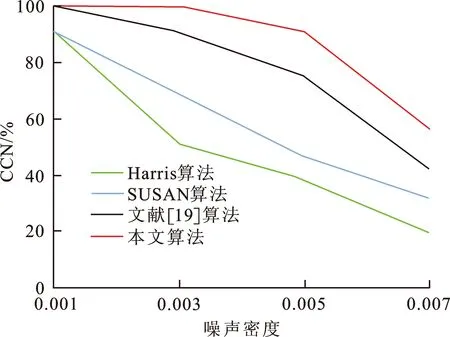
(b) 真实图像抗椒盐噪声的CCN变化曲线

(c) 模拟几何图像抗高斯噪声的CCN变化曲线

(d) 真实图像抗高斯噪声的CCN变化曲线图 9 不同算法的角点检测一致性CCN变化曲线Fig.9 Change curves of CCN of corner detection from different algorithms on images

4 结 语

为了提高角点检测的准确性,增强角点检测的抗噪性,借鉴Harris算法和SUSAN算法的思想,提出了一种基于图像邻域灰度变化的角点检测改进算法。改进算法中可以检测X型、T型、Y型3类角点,通过角点初筛,可有效地降低角点检测的时间开销。基于USAN模板内的分布离散度和非极大值抑制法,定位角点,在有效消除伪角点的同时,避免角点漏检。这为目标的重建、跟踪、识别等处理奠定了基础。后续将对本文改进算法做进一步优化,提升角点检测的自适应性和实时性。