多相剪切增稠液的流变性能

田明月,孙润军,王蕊宁,王秋实,陈美玉

(西安工程大学 纺织科学与工程学院,陕西 西安 710048)

0 引 言

剪切增稠液(STF)是一种胶质悬浮液的非牛顿可逆流体, 当剪切速率或剪切应力发生变化时,其黏度就会随之发生变化,且随剪切速率的增加而增加[1]。具有这种现象的流体因为粒子团聚等缺陷会破坏生产设备、阻碍输送管道等,给生产造成不利影响[2]。STFs的这种特性,在防刺领域具有广泛的应用前景。近年来关于单分散相剪切增稠液的研究较多, 对于多相剪切增稠液的研究主要集中于防弹衣的抗冲击性能、工业设备的减振性能等方面。多相剪切增稠液(STFs)具有广阔的应用范围,比如摩托车头盔、运动防护眼镜、防刺服等[3-4]。

为了使防刺复合材料的性能更加优异，与高性能纤维织物复合的多相剪切增稠液(STFs)需要具备良好的增稠效果。影响STFs流变行为的因素很多,如粒径、颗粒硬度、粒径比、分散介质、温度等[5],SiC颗粒粒径较小、硬度很大,所以常选取SiC作为第二分散相[6-7]。为了探索第二分散相SiC的加入对剪切增稠液流变性能的影响规律,为STFs的应用提供新的经验, 文中采用PEG200与SiO2制备单相剪切增稠液,再加入不同质量分数的SiC进行复配,制备多相剪切增稠液,并研究其稳态与动态流变性能,为后期浸渍高性能纤维织物,制备具有较好防刺性能并且舒适、轻便的防刺服装提供参考。

1 实 验

1.1 材料与仪器

1.1.1 材料 气相二氧化硅(SiO2，粒径50 nm,比表面积150 m2/g,阿拉丁工业公司)，碳化硅(SiC，粒径50 nm，上海巷田纳米材料有限公司)，聚乙二醇(PEG200,分散介质，平均分子量200，天津市科密欧化学试剂有限公司)，无水乙醇等(天津市富宇精细化工有限公司)。

1.1.2 仪器 FX-1200GD型电子天平(日本爱安德),CQ-25-6B型超声波清洗器(上海新超超声波仪器有限公司),MCR302型高级旋转流变仪(奥地利安东帕有限公司),DZF型真空干燥箱(北京科伟永兴仪器有限公司),101 型电热鼓风干燥箱(北京市永光明医疗仪器有限公司)。

1.2 分散体系的制备

将分散相SiO2粒子、SiC粒子与分散介质PEG200充分混合后加入无水乙醇 (超过STF的1.5倍),再放入超声波清洗器中振荡,分散均匀后置于真空干燥箱中干燥,除去多相剪切增稠液中的气泡和多余的无水乙醇,得到稳定的STFs分散体系。

1.3 流变性测试

在温度为25 ℃条件下,利用MCR302高级旋转流变仪测试STFs的动态和稳态流变性能。使用锥板夹具,转子的型号是CP25-2,板直径为25 mm,锥弧度为2°。稳态剪切扫描速率范围为0.01～10 000 s-1,测定流体黏度随剪切速率的变化曲线;在恒定频率为10 Hz,应变为0.1%～10 000%的范围内进行动态应力扫描。为了使样品建立其平衡结构并消除以往的剪切历史,在每次测量前均以10 s-1的剪切速率进行180 s的稳定预剪切。

2 结果与讨论

2.1 稳态流变性能

2.1.1 单相SiO2/PEG200分散体系 根据文献[8]制备STF的最优化配方,当SiO2的质量分数为26%,PEG200的质量分数为74%时,分散体系具有较好的剪切增稠效果。以此作为基础体系,在添加颗粒添加剂的STFs实验中,二氧化硅的质量分数保持在26%不变。图1为黏度-剪切速率的对数函数曲线。圆形表示剪切速率由小到大,正方形表示剪切速率由大到小。

图 1 SiO2/PEG200黏度-剪切速率曲线

从图1可看出,不论剪切速率增加还是减小,两条曲线的变化趋势是一致的,都存在剪切变稀和剪切增稠的现象,说明该分散体系具有可逆性。随着剪切速率的变化,分散体系的黏度也随之发生变化。初始剪切速率0.01 s-1,此时体系处于平衡状态;随着剪切速率的增加,分散体系的黏度逐渐降低,出现一段剪切变稀的范围;到达临界剪切速率,试样黏度会突然增加,从0.8 Pa·s增加到52 Pa·s,表现为剪切增稠行为。

2.1.2 多相SiO2、SiC、PEG200分散体系 图2是在基础体系上加入1.5%SiC的STFs的黏度和剪切速率的对数函数曲线。剪切速率为114 s-1时,体系黏度急剧增加,说明出现了剪切增稠行为。原因是在STFs分散体系中,分散相SiO2团聚体表面有大量的硅烷醇基(Si—OH),分散介质PEG的分子链上有羟基和醚氧基,当SiO2颗粒分散到PEG中时,硅烷醇基就会与羟基发生作用形成氢键[9],纳米SiC具有亲水性,粒径较小,三者之间形成较为稳定的分散体系。在初始剪切速率为0.01 s-1,无外力作用时,由于流体作用力断裂的氢键和因为粒子间作用力形成的氢键存在着一种动态平衡,体系的初始黏度为16.9 Pa·s。随着剪切速率的增加,氢键断裂的速度加快,此时由于剪切力较小,破坏的空间结构在分子间作用力下会很快修复,黏度变化不明显。随着剪切速率的进一步增加,当氢键成键的速度小于断裂的速度时,空间结构就会遭到破坏,形成一些相对孤立的SiO2和SiC团聚体,黏度明显下降,表现为剪切变稀现象。到达临界点后,此时临界剪切速率114 s-1,临界剪切黏度是1.43 Pa·s,体系中的主导力是流体作用力,体系中孤立的SiO2和SiC团聚体就会在流体作用力下二次团聚形成“粒子簇”[10-11],流体受到的阻力也会明显增加,使得分散体系中的黏度突然增大至91.3 Pa·s。

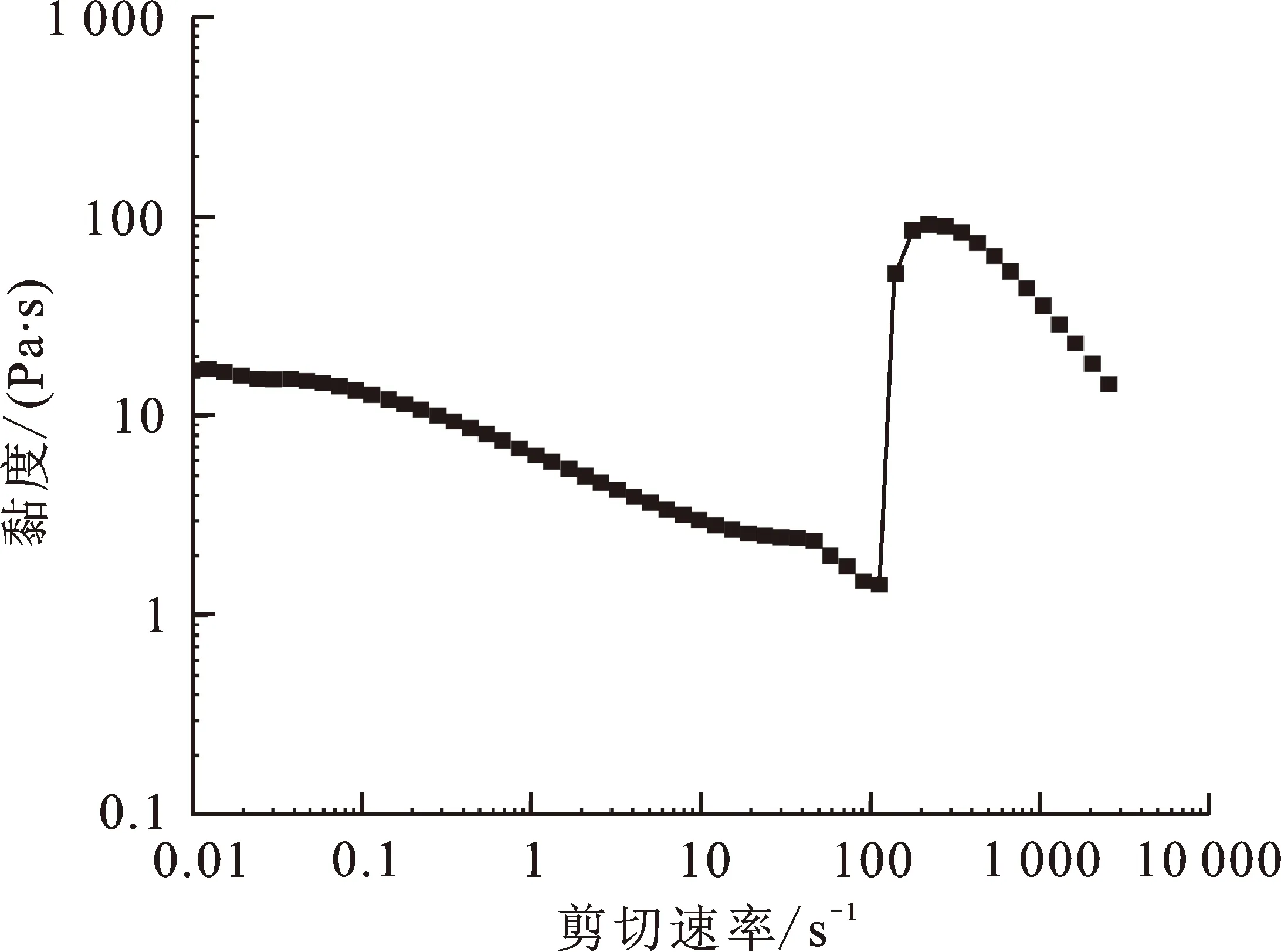
图 2 STFs的黏度-剪切速率曲线Fig.2 Viscosity-shear rate curve of STFs

分散相粒子为SiO2、SiC的STFs的宏观剪切增稠现象如图3所示。烧杯静置在桌面上,在平衡状态下,无外力作用时,光泽类似于胶体,颜色呈现灰色,呈现出较好的流动性。如图3(a)所示，当玻璃棒从烧杯中缓缓提起时,几乎感受不到任何阻力,说明STFs与玻璃棒之间的摩擦力相对较小,STFs会逐渐的流回烧杯中,可以看到明显的流线和光泽。如图3(b)所示，用玻璃棒猛戳烧杯中的STFs,发现STFs会很快变硬,呈现出类似于固体的特性,阻止玻璃棒继续进入STFs。抽出玻璃棒后,玻璃棒接触的地方及其周围的一定区域内呈现下沉的痕迹,但很快消失并重新恢复到原始悬浮液状态。由此可见,从宏观上看,剪切速率发生变化,STFs的黏度也随之改变,并且这种变化是可逆的,说明它是一种非牛顿可逆流体。剪切增稠液的宏观流变现象与上述微观增稠现象结果一致。

(a) 缓缓提起

(b) 迅速戳进

2.1.3 SiC含量对流变性能的影响 图4是SiC粒子含量对稳态流变性能的影响。由图4可知,4条曲线整体变化趋势基本一致。随着剪切速率的增大,体系黏度先减小,到达临界剪切速率后,黏度急剧增加,标志着出现了剪切增稠效果，说明SiC的加入能够提高体系的黏度。随着SiC含量的增加,起始黏度和最大黏度增大,原因是随着SiC粒子含量的增加,STFs悬浮液中SiC粒子和SiO2粒子碰撞团聚的机会增多,形成的“粒子簇”增大,体系的阻碍作用力增加。STFs 体系临界剪切速率随着纳米SiC粒子含量的增加而减小,说明体系在较小的剪切速率下就可以发生剪切增稠现象。然而,与SiO2单相剪切增稠液相比,第二相的加入会使临界剪切速率增大。可能由于悬浮液中添加颗粒的增多会阻碍粒子的扩展运动,形成“粒子簇”的响应就会延长,SiO2的接触网络形成的可能性减小,对稳定均匀的分散体系造成了一定的破坏[12]。

图 4 不同SiC含量的黏度-剪切速率曲线Fig.4 Viscosity-shear rate curves of different SiC contents

为了进一步表征剪切增稠效果,采用不同的参数描述STFs[13]。增稠周期(PT)为临界剪切速率与增稠点后最大黏度剪切速率的差值[14],即

(1)

表1,2分别为不同 SiC 含量分散体系剪切速率和黏度的测试结果。试样A、B、C、D中SiC质量分数分别为 0.5%, 1.0%, 1.5%和0%。 由表1可以看出, 随着 SiC 含量的增加, 增稠周期逐渐缩短, SiC 含量为1.5%时,增稠周期最短，为108。 即灵敏度较高,能够很快达到最大黏度, 抵抗施加的外力冲击。 单相 SiO2分散体系的增稠周期为184,介于 SiC 含量为1%和1.5%的增稠周期之间。

表 1 不同SiC含量分散体系剪切速率比较

增稠比(RT)为在临界剪切速率下,超过增稠点的最大黏度与临界黏度的比值[15-16],即

RT=ηmax/ηcr

(2)

式中:ηmax为超过增稠点悬浮液的最大黏度;ηcr为临界剪切速率下悬浮液的黏度。

由表2可以看出,单相SiO2分散体系的增稠比最大。此外，增稠比随着SiC含量的增加逐渐增大。SiC含量为1.5%时,STFs体系的增稠比比较大,增稠比为63.8,能够很好地阻碍流体作用力。

表 2 不同SiC含量分散体系黏度比较

2.2 动态流变性能分析

2.2.1 模量、复合黏度与应变的关系 图5是SiC含量为1.5%的SiC、SiO2、PEG200的多分散体系,在频率为10 Hz(即剪切速率10次/s)时,体系的储能模量(G′)、耗能模量(G″)以及复合黏度(η*)随应变的对数函数变化图。从图5可以看出,在研究的应变范围内,G″总大于G′。STFs体系的变化趋势分为3个区域:首先为线形黏弹区,随着应变的增加,模量基本不变;此后为剪切变稀区,模量随着应变的增加而减小,并达到最低值;最后为剪切增稠区,随着应变的进一步增大,模量增加,达到最大值,并且最大值都高于体系的初始值。

图 5 G′，G″以及η*与应变的关系Fig.5 Relationship between G′，G″，η* and strain

黏弹性理论[17]指出,弹性是分散体系中的固体行为,可以用储能模量G′表示,黏性是分散体系中的液体行为,可以用耗能模量G″表示。复合黏度η*表示物质对动态剪切的总阻抗,由表示弹性成分的储能黏度η″和表示黏性成分的动态黏度η′两部分组成。在较低的应变下,G′，G″和η*保持基本不变。原因是由于外力作用较小,网络结构能够在粒子的布朗运动和分子间作用力的共同作用下很快恢复,模量和复合黏度基本保持定值。随着应变的增加,表现为剪切变稀,G′的下降程度大于G″,原因是破坏的结构无法在二者的作用下恢复正常。表现为G′的值明显减小,而G″和η*相对比较稳定,只有轻微降低。当应变达到临界值202%时,G′和G″达到最低值,此时流体作用力与粒子的布朗运动和分子间作用力达到一种相对平衡的状态[18-19]。随着应变的进一步增大,流体作用力成为主要作用力,会形成“粒子簇”,使得G′，G″迅速增加,对外界产生的抵抗能力增加,也使得η*迅速增大。整个体系是以耗能为主,表现为黏性行为占主导地位。

2.2.2 分散相含量与应变的关系 图6是在基础体系的基础上加入不同比例SiC的STFs体系储能模量G′、耗能模量G″与应变的对数函数关系。

(a) 储能模量与应变的关系

(b) 耗能模量与应变的关系

从图6中可以看出,所有曲线中,储能模量与耗能模量随着应变的增加大都呈现先减小后增加的趋势。应变较小时,耗能模量几乎不受应变的影响,直到应变到达临界点后,耗能模量急剧增加。应变小于10%时,储能模量趋于平稳,而后明显减小,一旦达到临界应变[20]点,就会急剧增加。

分散体系中SiC的含量会对模量造成一定的影响。在应变相同的条件下,SiC含量较多的体系,具备更高的储能模量和耗能模量,呈现整体上移的趋势。随着SiC含量的增加,临界剪切应变会减小,剪切增稠行为更加明显。储能模量和耗能模量的最大值差异超过2个数量级,原因可能是SiC粒子的增加使得体系黏度增大,形成的相对孤立的团聚体比较接近,容易发生增稠行为。

3 结 论

以陶瓷颗粒中的碳化硅(SiC)颗粒作为STFs添加剂,研究悬浮液的流变特性。SiC颗粒的加入会使得STFs体系的黏度增加。

(1) 稳态流变实验表明,STFs具有可逆的剪切变稀和剪切增稠现象。随着SiC含量的增加,临界剪切速率减小,增稠周期缩短,增稠比增大；剪切速率大于临界剪切速率时,各体系都具有明显的剪切增稠现象。

(2) 动态流变实验表明,在所研究的应变范围内,分散体系中耗能模量大于储能模量,以耗能为主。体系主要表现为黏性,模量随着SiC含量的增加有所提高。

(3) 与SiO2单相剪切增稠液相比,SiC颗粒对悬浮液的增稠机理有一定的破坏作用。但是，添加剂SiC颗粒为改变STFs的增稠阶段提供了机会,可以通过控制增稠周期、增稠比、临界剪切速率等，在不同的范围控制增稠机理,拓展该智能流体的应用领域。