基于多源信息融合的分布式词表示学习
2019-10-22冶忠林赵海兴
冶忠林,赵海兴,张 科,朱 宇
(1. 青海师范大学 计算机学院,青海 西宁 810008;2. 陕西师范大学 计算机科学学院,陕西 西安 710062;3. 青海省藏文信息处理与机器翻译重点实验室,青海 西宁 810008;4. 藏文信息处理教育部重点实验室,青海 西宁 810008)
0 引言
表示学习是机器学习中的一个重要研究方向,表示学习的结果可直接输入各类机器学习任务中,用于提升其算法性能[1]。目前表示学习研究主要致力于网络表示学习[2]、词表示学习[3]和知识表示学习[4]等任务。其中,清华大学刘知远老师项目组在该三个领域都取得诸多的研究成果[5-6]。分布式表示最早由Hinton提出[7],分布式词表示学习旨在通过算法学习得到词语的一种压缩的、稠密的、低维度的特征向量,最终得到的向量可简称为词表示、词嵌入、词向量等。词向量可以反映出词语之间的语义、上下文等关系[8]。其中最经典的算法为Mikolov等[9-10]提出的Word2Vec模型。
目前,分布式词表示学习主要研究如何基于神经网络的方法改进词表示在词相似度和词类推任务中的性能,也取得了丰富的研究成果。例如,倾向于主题共性的TWE算法[11]、利用句法分析优化的DEPS方法[12]、基于多原型词嵌入的Huang方法等[13]。基于神经网络的词表示学习算法也存在如下不足: (1) 罕见词由于语料匮乏而得不到充分的上下文词语对共现,进而无法准确有效地训练出其表示向量。(2) 某些语义相反的词语出现于相互上下文时,可使意义相反的词语由于更多的上下文词语对共现,而形成更相近的表示空间距离。(3) 意义相近的两个词语假如均不出现于对方的上下文窗口时,可使训练得到的两个同义词表示向量在词向量空间中具有较远的距离。
本文提出了一种融合多源信息的词表示学习算法(MSWE),该算法旨在将词语的语义描述和同义词与反义词等外部资源信息融入词表示学习模型中,使得学习得到的词表示向量蕴含更多的信息,而不仅仅是词语的上下文等结构信息。
首先,本文构建了一个同义词与反义词词典(Synonyms and Antonyms Directory, SAD),在词表示模型学习的过程中基于同义词与反义词词典SAD明确地提示某些上下文词语对是同义词,某些词语对是反义词,此种行为使得同义词的词嵌入在向量表示空间上具有更相近的空间距离,而反义词的词嵌入则在向量表示空间上具有更远的空间距离。另外,罕见词由于缺少充足的上下文词语对,导致了模型训练不充分,但SAD词典通过添加同义词与反义词信息,给予罕见词更多的特征信息。因此,可有效优化神经网络词表示学习模型中存在的三个不足。
其次,本文从维基百科和在线英语词典中抽取了词语的解释和描述文本作为词语的属性文本。该属性文本是有别于上下文结构的内在语义信息,也可称之为词语的属性语义文本。在语言模型中,罕见词由于缺乏上下文词语的贡献,从而得不到充分的训练,如果使用上述属性语义文本则可有效地弥补因为结构特征稀疏而导致的罕见词训练不充分问题。对于非罕见词,属性语义文本也能提供丰富的参考特征,从而优化词表示学习过程。对于反义词出现于上下文窗口且同义词未出现于上下文窗口的不足,属性语义文本也能根据词语的内在语义信息判断,诱导词表示学习模型训练。因此,通过构建词语的属性语义文本可有效地解决神经网络词表示学习中存在的三个不足。
再次,现有的词表示学习常用的方法是在Word2Vec的目标函数后面添加一些约束项。而基于矩阵分解思想进行研究和改进的工作较少。由于,Levy和Goldberg证明了Word2Vec的实质是隐式地分解添加了负采样的非负点互信息矩阵。因此,本文采用了诱导矩阵补全(Inductive Matrix Completion, IMC)的矩阵分解算法训练语言模型,该模型是一个多资源融合学习的模型,可通过两个辅助矩阵优化目标矩阵的分解。
基于以上的处理,本文提出的算法可有效解决基于神经网络的词表示学习中存在的三个不足,即通过同义词与反义词词典、属性语义文本和诱导矩阵补全算法,罕见词、同义词和反义词被优化三次。另外,通过显式地构建SAD词典,以及词语的解释和描述文本,可有效提升词表示学习算法在词相似度评测任务中的性能。
1 相关工作
词语表示学习最简单的是独热表示(One-hot Representation)[14],独热表示存在表示维度高、数据稀疏、无法反映语义信息等缺陷,进而无法进行词语之间的语义计算。而分布式词表示学习可以完全解决该问题。因为分布式词表示学习方法一般通过神经网络将词语与其上下文词语之间的关系压缩到一个低维度的向量表示空间中,该压缩机制的提出完全是模拟了人脑中神经元的工作机制。压缩后词表示向量中的每一个维度均与词语的某种结构存在关联关系,例如,文献[15-17]对词表示向量中单维度的实际意义进行了开创性的研究。
基于神经网络训练词向量也经历了从复杂到简单、从低效到高效的发展历程。例如,Bengio[6]于2006年提出了神经网络概率模型(Neural Probabilistic Language Model, NPLM),该模型开创了使用神经网络训练词向量的先河。需要注意的是,最早将分布式词向量应用于实际任务的是Miikkulainen和Dyer[18]。但是,NPLM训练约1千万的词语,需要耗时3周左右。因此,在文献[19-22]中Bengio、Goodman、Hinton、Mnih等人对NLPM的优化提出了不同的方案。Mikolov等[9-10]将词向量学习和语言模型学习分步训练,从而提出了Word2Vec模型,Word2Vec被广泛应用于文本分类[23]、分词[24]、情绪分类[25-26]等领域。随后,短语[27]、句子[28]、文档[29]等的表示学习算法被相继提出。
随后,Levy和Goldberg[30]证明了Word2Vec的实质是隐式地分解添加了负采样的非负点互信息矩阵(Shifted Positive Pointwise Mutual Information, SPPMI)。如果该矩阵删除了负采样系数(不考虑负采样),则变成了非负点互信息矩阵(Positive Pointwise Mutual Information, PPMI)。获得了词语和上下文词语之间的PPMI矩阵,可较方便地计算得到Shifted PPMI(SPPMI)矩阵。分解PPMI矩阵和SPPMI矩阵则可得到每个词语的分布式表示向量。Levy和Goldberg在文献[31]中验证了使用奇异值分解(Singular Value Decomposition, SVD)PPMI在部分数据集上词表示的性能优于SGNS,但是在有些数据集上性能恰好相反。在文献[27]中,使用SVD分解SPPMI矩阵在词相似度任务上性能均优于SGNS。文献[32-33]中,Hamilton等认为如果想要精准地得到词表示向量,SVD方法应该为首选,而非SGNS。
2 本文方法
2.1 MSWE算法介绍
在神经概率模型中,词表示学习的目标是最大化词语序列的出现概率,如式(1)所示。
(1)
但上述计算复杂度非常高,随后,Mikolov等[9-10]提出了CBOW和Skip-Gram两种词表示训练模型。Mikolov等同时提出了两种优化加速方法: 层次化的Softmax(Hierarchical Softmax, HS)和负采样(Negative Sampling, NS)。基于NS优化的Skip-Gram可简称为SGNS。
在文献[30]中已经证明,SNGS建模的过程为隐式地分解特征矩阵的过程。该特征矩阵可通过点互信息(Pointwise Mutual Information,PMI)矩阵进行构建。
PMI主要是用来衡量两个变量之间的相关性,其定义如式(2)所示。
(2)
log取自信息论中对概率的量化转换。在自然语言处理等任务中,Church和Hanks[34]首次将PMI矩阵引入到计算词语相似度任务中[35]。因此,PMI也可以衡量两个词语之间的相关性,其可定义为式(3)所示。
(3)
其中,#(w,c)为词语w和上下文c在整个语料上出现的次数。
Levy等在文献[30]中将PMI矩阵重新定义为式(4)所示。
(4)
式(4)在式(3)的基础上乘了|D|(总词语个数),避免PMI的值太小。
Levy等在文献[30]中证明了语言建模中SGNS模型的实质为矩阵分解,如式(5)所示。
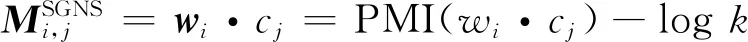
(5)
其中,k为负采样,通过设置k值可以调节在矩阵分解的过程中负采样对词表示性能的影响。由于式(5)会出现如下情形:
PMI(w,c)=log 0=-∞
(6)
因此,在自然语言处理中,可用PPMI矩阵替换PMI矩阵,其定义如式7所示。
PPMI(w,c)=max{PMI(w,c),0}
(7)
最终,Levy等[30]结合式(5)和式(7)提出了一种新的基于矩阵分解的词表示学习算法,该算法显式地分解SPPMI矩阵,该矩阵定义为式(8)所示。
SPPMI(w,c)=max{PMI(w,c)-logk,0}
(8)
至此,文献[30]提出了PMI矩阵、PPMI矩阵和SPPMI矩阵,它们的定义如式(9)~式(11)所示。
式(9)中,PMI矩阵中会出现元素值为负无穷的情形。式(10)中,PPMI矩阵中未考虑SGNS中的负采样数k。式(11)中,SPPMI矩阵既能避免元素值为负无穷的情形,又能融入SGNS中的负采样k。因此,为了更好地获得每个词语的表示向量,Levy等[30]使用了SVD方法对SPPMI矩阵进行分解,即MSPPMI≈U·Σ·VT,此时每个词语的表示向量可定义为式(12)所示。
WSVD=U·Σα
(12)
Caron[36]建议为了获得更好性能的词向量,应该仔细调整α的值。Levy等[30]设置了α为0.5。
文献[32-33]建议在基于矩阵分解的词表示学习任务中应该尽量使用SVD获得高性能的词表示向量。但是SVD算法是一个单纯的矩阵分解算法,该算法与本文的设想有些差别,因此,本文希望借助协同过滤的思想实现多源数据特征协同分解,从而使得学习得到的词表示中蕴含各个辅助矩阵中有价值的特征信息。
基于本文收集的同义词与反义词信息,可以较方便地构建同义词与反义词矩阵(Synonyms and Antonyms Matrix, SAM)。基于本文收集的词语属性文本,进而较方便地构建词语语义特征矩阵(Semantic Feature Matrix, SFM)。式(11)详细介绍了如何构建上下文特征矩阵(Context Feature Matrix, CFM)。SFM矩阵能够反映词语之间的属性语义关联,CFM矩阵能够反映词语之间的结构语义关联。SAM矩阵可以使同义词的嵌入在向量空间上具有更相近的空间距离,使反义词的嵌入在向量空间上具有更远的空间距离,而非同义词和非反义词却不受影响。
至此,本文算法的难点在于如何将SAM、SFM和CFM三个特征矩阵进行联合学习。恰巧的是,Natarajan和Dhillon[37]在2014年提出了一种新的诱导矩阵补全(Inductive Matrix Completion, IMC)算法。 IMC算法使用了基因特征辅助矩阵X∈d1×m和疾病特征辅助矩阵Y∈d2×n去分解基因-疾病目标矩阵M∈m×n。IMC的目标函数定义如式(13)所示。
(13)
由式(13)可知,IMC算法的实质也是矩阵分解,但是在矩阵分解的过程中,从矩阵X∈d1×m和矩阵Y∈d2×n中学习有价值的特征嵌入到矩阵W∈k×d1和矩阵H∈k×d2中,最终使得矩阵M∈m×n满足M≈XTWTHY。
综上所述,本文使用诱导矩阵补全算法融合学习SAM、SFM和CFM三个特征矩阵,使用WTH作为每个词语的表示向量。对于集成学习,最直接的设想是将CFM矩阵设置为IMC算法中待分解的目标矩阵M∈m×n,将SAM特征矩阵设置为IMC算法中的矩阵X∈d1×m,将SFM特征矩阵设置为IMC算法中的矩阵Y∈d2×n,该算法被称为基于多源信息融合的分布式词表示学习算法(MSWE)。为了提升性能,本文基于IMC算法尝试了另外6种特征学习方式,其基本流程将在“实验与分析”一节展开详述。另外,我们通过分析可以发现,SAM和SFM的准确构建与否直接影响着CFM分解后WTH在词相似度等任务中的表现性能。
2.2 上下文特征矩阵(CFM)构建
首先将所有的相似度测试集中的单词放入到一个文本中,并对该文本中的词语做去重处理,得到由测试集构成的相似度词典S,S的大小为5 987,且si∈S,i<=|S|。
本文下载了最新版本的全部英文维基百科语料(1)https: //dumps.wikimedia.org/。SGNS算法在训练语言模型时需要每个词语以空格的方式分割,由于英文自带空格作为分隔符,因此将全部的维基百科语料输入到SGNS模型便可以训练得到语言模型。本文的目标是更好地分解上下文特征矩阵CFM,因此首先需要构建出稳健的CFM特征矩阵。整个英文维基百科语料有数千万个词语,而基于矩阵分解的算法计算数千万词语的表示向量具有较高的运算复杂度,因此,本文仅考虑如何训练出相似度词典S中每个词语的表示向量,即仅考虑5 987个词语。综上,CFM特征矩阵构建可分为两个部分。
(1)上下文特征文本预处理(a)从下载的英文维基百科语料中抽取出正文文本,并删除所有的HTML标记等噪声数据; (b)将正文文本中的大写单词和大写字母全部转化为小写; (c)将正文文本中的数字全部转化为特殊符号“NUMBER”; (d)将正文文本以逗号、问号、感叹号断行,即每行一条文本; (e)如果该行文本中包含有相似度词典S中的任意一个词语,则保留该条文本,否则删除该条文本。最终保留的文本有3 770 834条。
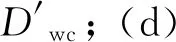
2.3 同义词与反义词特征矩阵(SAM)构建
在网络资源中,有较多的网站可以获取词语的同义词和反义词等信息。本文使用Thesaurus(2)http: //www.thesaurus.com/提供的同义词与反义词数据。构建SAM特征矩阵的具体步骤如下:
(1)同义词与反义词爬取使用爬虫技术,利用“http://www.thesaurus.com/browse/+关键词+?s=t”作为爬取内容的链接,爬取之后的内容为含有HTML标记的文本,因此需要对该文本做提取同义词与反义词的操作。经过分析发现,该文本中含有同义词与反义词的文本行为json格式的数据。因此仅需要解析json数据就可以提取得到相似度词典中每个词语的同义词和反义词列表。

2.4 属性语义特征矩阵(SFM)构建
SFM特征矩阵可被认为是词语之间的结构语义关联,该语义信息是由词语与上下文词语之间的结构特征所反映出来的。具体构建过程如下:
(1)语义文本爬取对于相似度词典S中的每个词语si做如下处理: (a)从英文维基百科页面中抽取词语的解释和描述文本,解释文本的起始标记为“si”,终止标记为“
(2)语义文本预处理(a)删除HTML等标记; (b)删除英文停用词; (c)得到每个si的语义文本,记为ST文件。
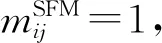
2.5 算法复杂度分析
本文训练词向量的目标函数为式(13),该目标公式来自于诱导矩阵补全算法。诱导矩阵补全算法通过两个辅助矩阵X∈d1×m和Y∈d2×n分解目标矩阵M∈m×n,分解后得到矩阵W∈k×d1和矩阵H∈k×d2中,本文使用WTH作为每个词语的表示特征矩阵。因此,本文的模型训练复杂度主要来自于诱导矩阵补全过程,该过程的算法复杂度为O((nnz(M)+md2+mk)k),nnz(M)表示M中非零元素的个数。
3 实验与分析
3.1 相似度词典预处理
在文献[12]中使用了6个词相似度数据集评测提出算法的性能,本文同样使用文献[12]中所采用的6个数据集,并和文献[12]提出的算法做对比,其中,WordSim353在多篇文献中被作为评测数据集[38-41]。WordSim353通常被拆分为WordSim Similarity和WordSim Relatedness两个评测数据集。另外,本文删除了相似度词典中的名词所有格词语和不能在网络资源中查询到解释或描述文本的词语,总共删除词语118个,最终在相似度词典中有剩余词语5 987个。评测数据集的具体信息如表1所示。
本文通过训练5 987个词语的表示向量,验证基于诱导矩阵补全的词语表示学习的可行性。本文算法首先在小规模的语料数据和词典知识上进行学习。而超大规模的矩阵分解一般是采用迭代和Map-Reduce[43]等分布式计算框架。另外,基于消息传递接口(Message-Passing-Interface, MPI)[44]可实现进程级别的矩阵分解并行算法。这些计算框架为大规模语料数据的表示学习提供了可能。
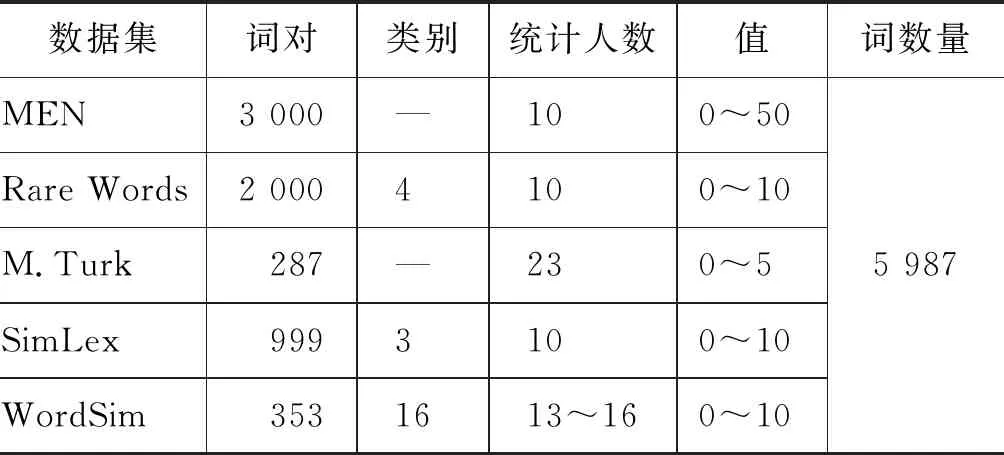
表1 词相似度评测数据集
3.2 实验设置
为了研究不同的融合方式对词表示的性能影响,本文提出了7类信息集成方法:
MSWE@CFM_SFM使用SVD将SFM特征矩阵降维为100,并作为IMC算法中的矩阵Y。CFM特征矩阵不降维且作为IMC算法中的矩阵M。IMC算法中的矩阵X设置为单位矩阵E。
MSWE@SAM_CFM_SFM使用SVD将SFM特征矩阵降维为100,作为IMC算法中的矩阵Y。CFM特征矩阵不降维且作为IMC算法中的矩阵M。SAM矩阵设置为IMC算法中的矩阵X。
MSWE@sam_CFM_SFM使用SVD将SFM特征矩阵降维为100,作为IMC算法中的矩阵Y。CFM特征矩阵不降维且作为IMC算法中的矩阵M。将SAM特征矩阵中的-1修改为0,且作为IMC算法中的矩阵X。
MSWE@CFM_sam_SFM使用SVD将SFM特征矩阵降维为100,作为IMC算法中的矩阵Y。CFM特征矩阵中设置同义词为1,反义词为0,其余元素值保持不变,变换后的CFM特征矩阵作为IMC算法中的矩阵M。IMC算法中的矩阵X设置为单位矩阵E。
MSWE@CFM_SAM使用SVD将SAM特征矩阵降维为100,且作为IMC算法中的矩阵Y。IMC算法中的矩阵X设置为单位矩阵E。
MSWE@CFM_SAM+SFM使用SVD将SFM特征矩阵降维为100,使用SVD将SAM特征矩阵降维为100,两个降维后的矩阵简单拼接后作为IMC算法中的矩阵Y。IMC算法中的矩阵X设置为单位矩阵E。
MSWE@CFM_SAM+CFM_SFM使用SVD将SFM特征矩阵降维为100,使用SVD将SAM特征矩阵降维为100,并分别使用IMC算法得到各自的词语表示,之后将两者的词语表示进行线性拼接。
以上算法是本文算法的7类数据融入尝试,MSWE@CFM_SFM和MSWE@CFM_SAM对比分析了将属性语义特征和同义词与反义词特征设置为IMC算法中的矩阵Y后对词语表示的影响,矩阵X设置为单位矩阵。MSWE@SAM_CFM_SFM和MSWE@sam_CFM_SFM对比分析了将同义词与反义词特征矩阵中的反义词设置为0或-1时对词语表示的影响。另外,MSWE@CFM_SAM+SFM和MSWE@CFM_SAM+CFM_SFM对比分析了先融合后分解与先分解后融合策略对词语表示的影响。为了验证本文提出的融合算法的性能,本文又引入了5类基于神经网络的词表示学习算法进行性能对比测试。例如,CBOW和Skip-Gram是Word2Vec[9-10]提出的两种语言训练模型,基于负采样优化的Skip-Gram简称为SGNS。DEPS是文献[12]所提出的算法,Glove是文献[42]所提出的方法,Huang是文献[13]所提出的算法。为了验证本文算法中引入的CFM、SFM和SAM是否有效,本文分别测试了它们在词相似度评测数据集上的表现,评测方法为保留原始维度长度和使用SVD降维到100维度时的性能。本实验中的设置为: 窗口大小为5,向量长度为100,λ为0.1。在构建SFM矩阵时,仅保留了词频大于等于2的词语。本文算法与其他各对比算法均在2.2节中处理所得的3 770 834条文本上进行实验。对比算法所采用的语料中不包含同义词与反义词信息以及解释文本等。
3.3 实验结果讨论
本节详细列出了每类算法在6类评测数据集上的性能表现,进而分析本文提出的算法为何能够在词语相似度评测中获得较好的性能。本文使用余弦相似度公式计算了两个词语之间的相似度值。本文同样使用余弦相似度衡量评测数据集中的人工标注的结果与本实验提供的相似度值之间的相关性,即人工标注的相似度值与计算所得的相似度值之间的余弦相似度值作为衡量算法优劣的评价指标。具体结果如表2所示。

表2 词表示学习算法性能对比分析
从表2可以看出,本文提出的多源数据融合的词表示学习算法中,有5类数据融合方式均能在6类词相似度评测数据集上获得优异的性能。尤其是在Rare Words和M Turk上性能的提升是最明显的。本文在之前内容中已经阐述过,SAM、CFM和SFM的性能直接影响特征融合的后词表示的性能。从表2中可以发现,SGNS和CBOW的性能基本一致。CFM为本文通过2.2节中的步骤构建出来的特征矩阵,由于CFM是SGNS隐式分解的目标矩阵,因此,SGNS和CFM在理论上是性能一致的。但是结果显示,CFM(未使用SVD分解)的性能略优于SGNS,尤其在Rare Words数据集上优势更明显,这说明基于构建矩阵的方法能够过滤掉一些噪声词汇。另外,本文构建的SFM特征矩阵的性能劣于SGNS,也劣于CFM(SVD)。CFM(SVD)和SFM(SVD)拼接后性能提升不明显,其性能稍优于CFM(SVD)的词表示性能,高于SFM(SVD)的词表示性能,这表明简单的向量拼接在一定范围内能带来性能上的提升。采用了基于诱导矩阵补全的数据特征融合算法后,MSWE@SAM_CFM_SFM和MSWE@sam_CFM_SFM的性能劣于SGNS,而其余5类特征融合方式却获得了优异的性能表现,这表明基于诱导补全的数据特征融合方式比简单的特征拼接更有效果。另外,基于该实验结构还发现,本文构建的同义词与反义词特征矩阵SAM,如果将其直接作为IMC算法中的矩阵X,不论是否将反义词之间的元素值设置为0或-1,均将获得较差的性能。但是如果将SAM特征矩阵降维后作为IMC中的矩阵Y,其性能较CFM与CFM(SVD)均获得了较大的提升。上下文特征矩阵CFM与属性语义特征矩阵SFM联合分解,不论是否将CFM中的同义词设置为1且反义词设置为0,其对结果的影响较小。另外,将CFM同SFM和SAM的其中之一联合分解,其性能均优于CFM,这说明将属性文本和同义词与反义词融入词表示得到的性能优于仅考虑上下文结构的词表示。MSWE@CFM_SAM+SFM和MSWE@CFM_SAM+CFM_SFM的实验结果表明,将SAM和SFM先使用IMC分解后线性拼接的性能优于将其先线性拼接后使用IMC分解。
综上分析,本文可得出如下结论:
(1) 将不同源的特征降维后,采用简单的拼接并不能得到词表示性能的较大提升。
(2) 比起拼接的策略融合多源数据特征,本文引入的诱导矩阵补全算法能够从融合的多源特征中学习到重要的数据特征,使得最终学习得到的词表示性能得到极大的提升。
(3) 如果方法得当,通过构建语言模型的SPPMI矩阵,其获得的词表示性能能够达到与基于神经网络的词表示等同或更优的性能。
(4) 在引入多源特征时,使用SVD降维后的特征比使用原始的特征更有效。例如,本文中使用的同义词与反义词特征矩阵SAM。
(5) 融合多源的数据特征构建出来的词表示的性能优于使用单一特征构建的词表示性能,因此,在词表示学习算法中,基于诱导矩阵补全的多视图集成学习是一种行之有效的方法。
3.4 参数分析
在构建词语的属性语义特征SFM时,并不是所有的词语都参与构建矩阵的过程,本文按照词频过滤掉了一些词频小于阈值的词汇。表3是爬取的属性语义文本中词频大于或者等于阈值的词语个数。

表3 属性特征文本中词语数量统计
如表3所示,语义文本中共有词语45 927个,词频大于或者等于2的词语在语义文本中共有22 744个,随着阈值的变大,参与构建矩阵的词语数量就越少。本文设置的词频过滤阈值为2、4、6、8、10、15、20。那么,通过不同阈值构建的SFM矩阵对词表示的性能影响又是如何呢?其分析结果如图1所示。

图1 词频过滤对SFM特征矩阵的性能影响
从图1可以看出,在6个词语相似度数据集上,设置词语表示长度为100,随着词频阈值设置越大,过滤掉的词汇就越多,在这种条件下构建出来的SFM特征矩阵在词语相似度任务上表现出来的性能就越差。当设置词频过滤阈值为2时,参与构建SFM特征矩阵的词语就越多,因此,得到的SFM特征矩阵的词表示性能就越好。
CFM(SPPMI)特征矩阵为SGNS的矩阵分解目标矩阵,因此,CFM(SPPMI)矩阵采用SVD降维后得到的词表示与SGNS算法获得的词表示是同种性质的,即同一种算法采用不同的方式实现而获得的词表示。SGNS是采用浅层的三层神经网络搭建的模型,采用随机负采样算法优化加速模型的拟合。CFM矩阵来源于SGNS的分解形式,因此为了保持形式一致,CFM(SPPMI)也保留了负采样值k的设置[式(8)]。此时的k可以被认为是负采样值的大小,也可以被认为是CFM(SPPMI)与SGNS之间的偏移量。图2展示了不同k值对CFM特征矩阵的词表示性能影响,k的取值为1、3、5、7、15、30。
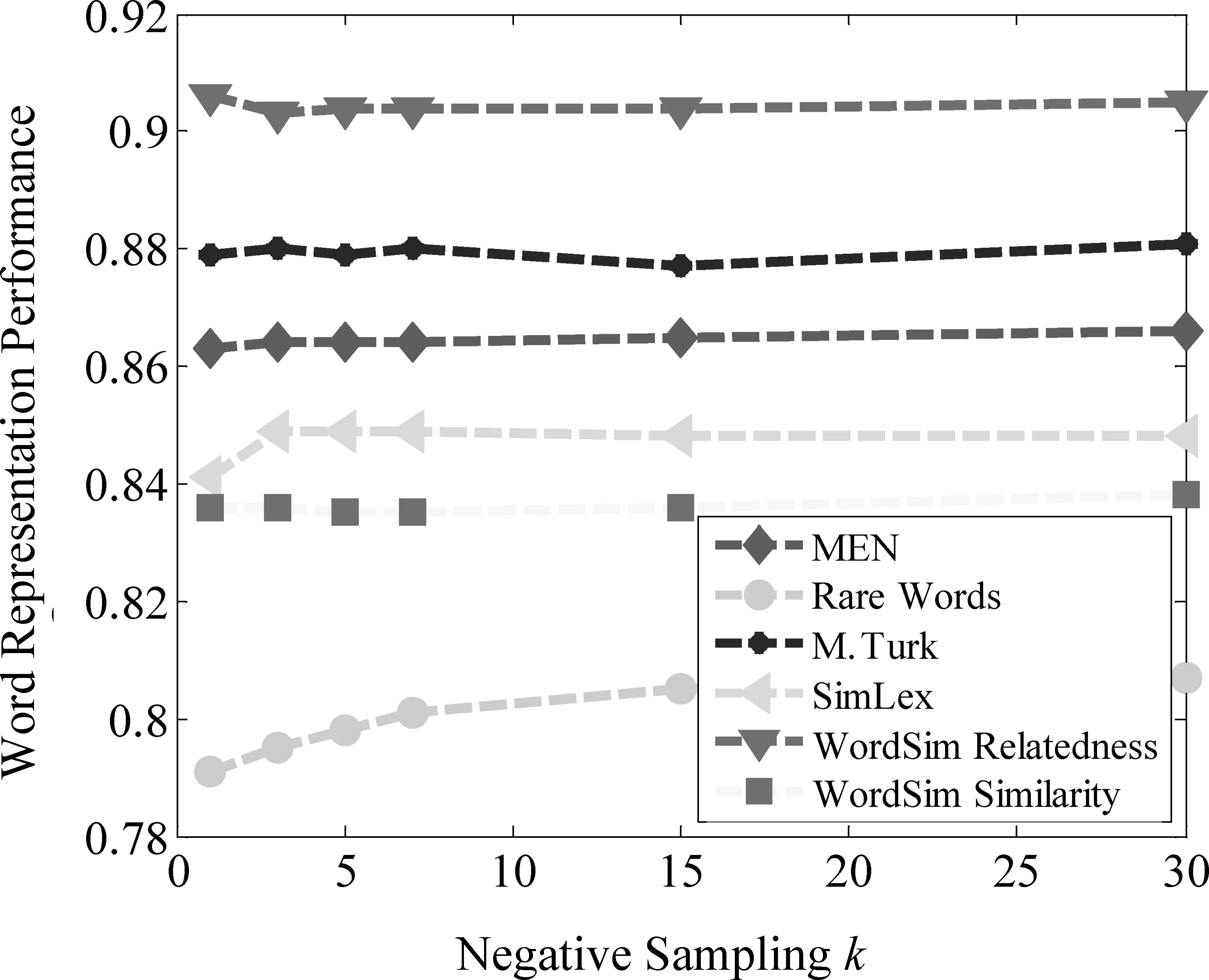
图2 负采样k对CFM(SPPMI)特征矩阵的性能影响
从图2可知,在Rare Words评测数据集上,设置词语表示长度为100,随着k值的不断变大,CFM(SPPMI)的词表示性能得到逐渐的提升。在其余5个词相似度评测数据集上,CFM(SPPMI)的性能提升得非常缓慢,总体来讲,当负采样为30时,CFM的性能肯定是优于负采样取值为1的情形。这种增长缓慢的原因是,随着负采样值取的增大,引入的噪声数据也越大,即使用的负样本也越多(不存在上下文关系的词语)。
从表2中可以发现,MSWE@CFM_SFM、MSWE@CFM_sam_SFM、MSWE@CFM_SAM和MSWE@CFM_SAM+CFM_SFM等的多源信息融合方式是行之有效的,且其性能在词语表示学习的相似度评测任务中均优于单一的结构特征模型,例如,SGNS、CBOW、Huang、Glove和DEPS等模型。但是上述实验是在词表示向量长度为100,且IMC算法中λ为0.1的设置下所得到的数据结果。因此,表4~表7中详细分析了词表示向量长度和式(13)中的λ在Rare Words评测集上对词表示性能的影响。的取值为30、50、100、150和200,λ的取值为10-1、10-2、10-3、10-4和10-5。
表4 MSWE@CFM_SFM的λ与影响分析
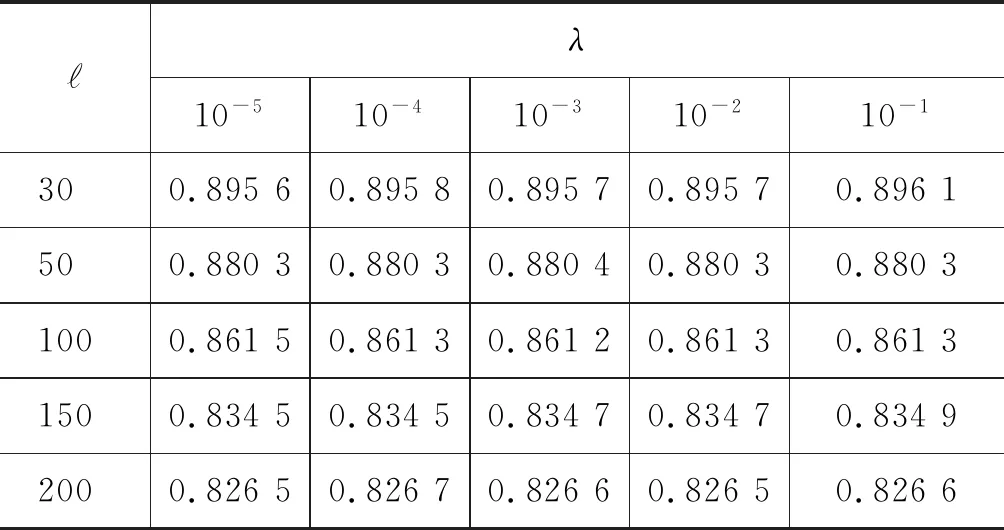
表4 MSWE@CFM_SFM的λ与影响分析
ℓλ10-510-410-310-210-1300.89560.89580.89570.89570.8961500.88030.88030.88040.88030.88031000.86150.86130.86120.86130.86131500.83450.83450.83470.83470.83492000.82650.82670.82660.82650.8266
表5 MSWE@CFM_sam_SFM的λ与影响分

表5 MSWE@CFM_sam_SFM的λ与影响分
ℓλ10-510-410-310-210-1300.89840.89840.89840.89840.8987500.88330.88330.88330.88330.88341000.85350.85350.85350.85350.85361500.83760.83760.83760.83760.83792000.82940.82940.82940.82940.8300
表6 MSWE@CFM_SAM的λ与影响分析
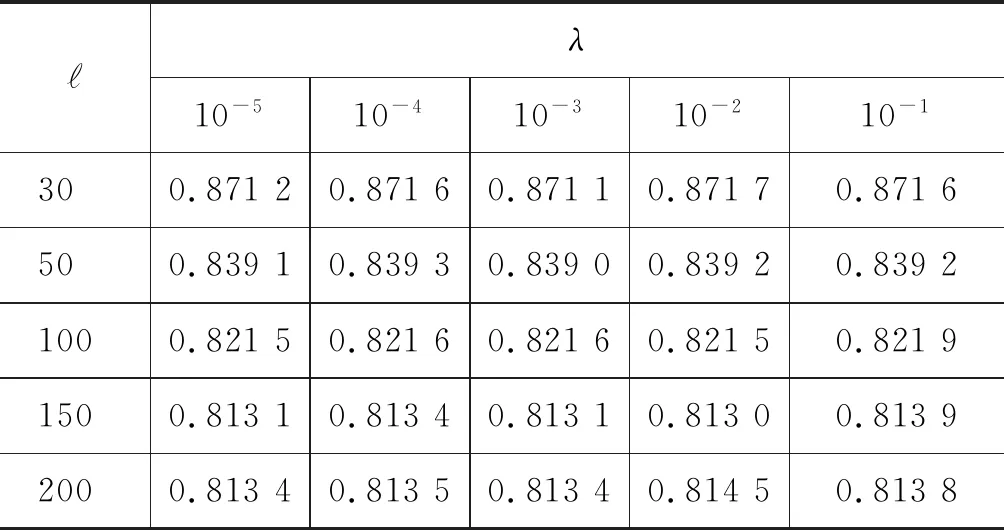
表6 MSWE@CFM_SAM的λ与影响分析
ℓλ10-510-410-310-210-1300.87120.87160.87110.87170.8716500.83910.83930.83900.83920.83921000.82150.82160.82160.82150.82191500.81310.81340.81310.81300.81392000.81340.81350.81340.81450.8138
表7 MSWE@CFM_SAM+CFM_SFM的λ与影响分析
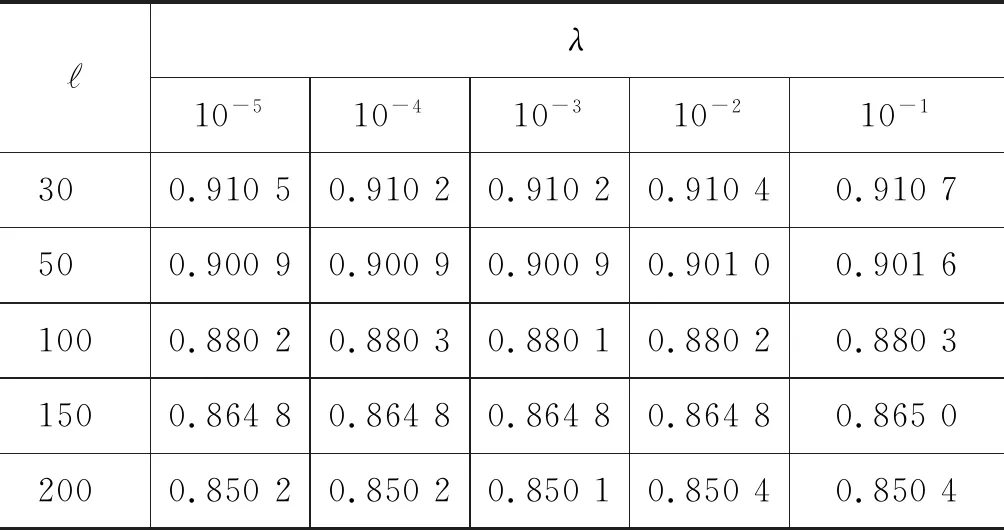
表7 MSWE@CFM_SAM+CFM_SFM的λ与影响分析
ℓλ10-510-410-310-210-1300.91050.91020.91020.91040.9107500.90090.90090.90090.90100.90161000.88020.88030.88010.88020.88031500.86480.86480.86480.86480.86502000.85020.85020.85010.85040.8504
在基于神经网络的词表示学习中,如果词向量的维数设置过大,会导致模型训练时间较长,但是向量中包含的特征信息较多。如果词向量的维数设置过小,虽然模型训练时间较短,但是词向量中包含的特征信息就较少。只有取得合适的词向量维度值,才能在词相似度和文本分类等评测任务中发挥出更好的性能。而在表4、表5和表6中,词向量的维度设置得越小,则在词相似度评测任务中表现出的性能越好。该结论和基于神经网络的词表示学习中关于维度的认识较为不同。在基于神经网络的词表示学习中,把当前词语与其上下文词语的结构关系嵌入到固定长度的向量空间时,过大或过小的向量维度会引起特征的冗余或丢失。此外,在不同的语料上,相同的算法可能取得的最佳维度也不相同。本文算法的实质是矩阵的联合分解,以当前词语与上下文词语构成的CFM特征矩阵为待分解目标矩阵,以同义词与反义词特征矩阵SAM和属性语义特征SFM作为辅助分解矩阵。在分解算法中,当较小的维度被选择时,分解算法往往会保留关键特征,同时删除冗余特征,此外,扩大了不同特征之间的差异性,以便于更好地为后续的应用服务。当然,过小的维度也同样会导致特征的严重丢失,导致在词相似度评测中表现出较差的性能。对于分解算法的维度,主要依赖于数据之间的相关性,即数据之间的关联性越强,则适合降维到更小的维度,如果数据之间的关联性较弱,则适合降维到更大的维度。本文主要是研究如何分解CFM特征矩阵,而该矩阵中的每个值均是词语之间的上下文关系。因此,降维的维度数越少,其词表示学习性能越好。
3.5 词表示可视化
词表示学习旨在学习得到词语的低维度向量表示。向量在高维空间中呈现出一条多维度的线,但是投影到二维的平面之后,呈现出点的效果。在该节实验中,本文将随机选取1 000个词语的表示向量,然后将它们投影到二维的平面上,从这些点表现出来的形状分析算法捕获了何种性质的词语特征。降维算法使用t-SNE算法,具体结果如图3所示。
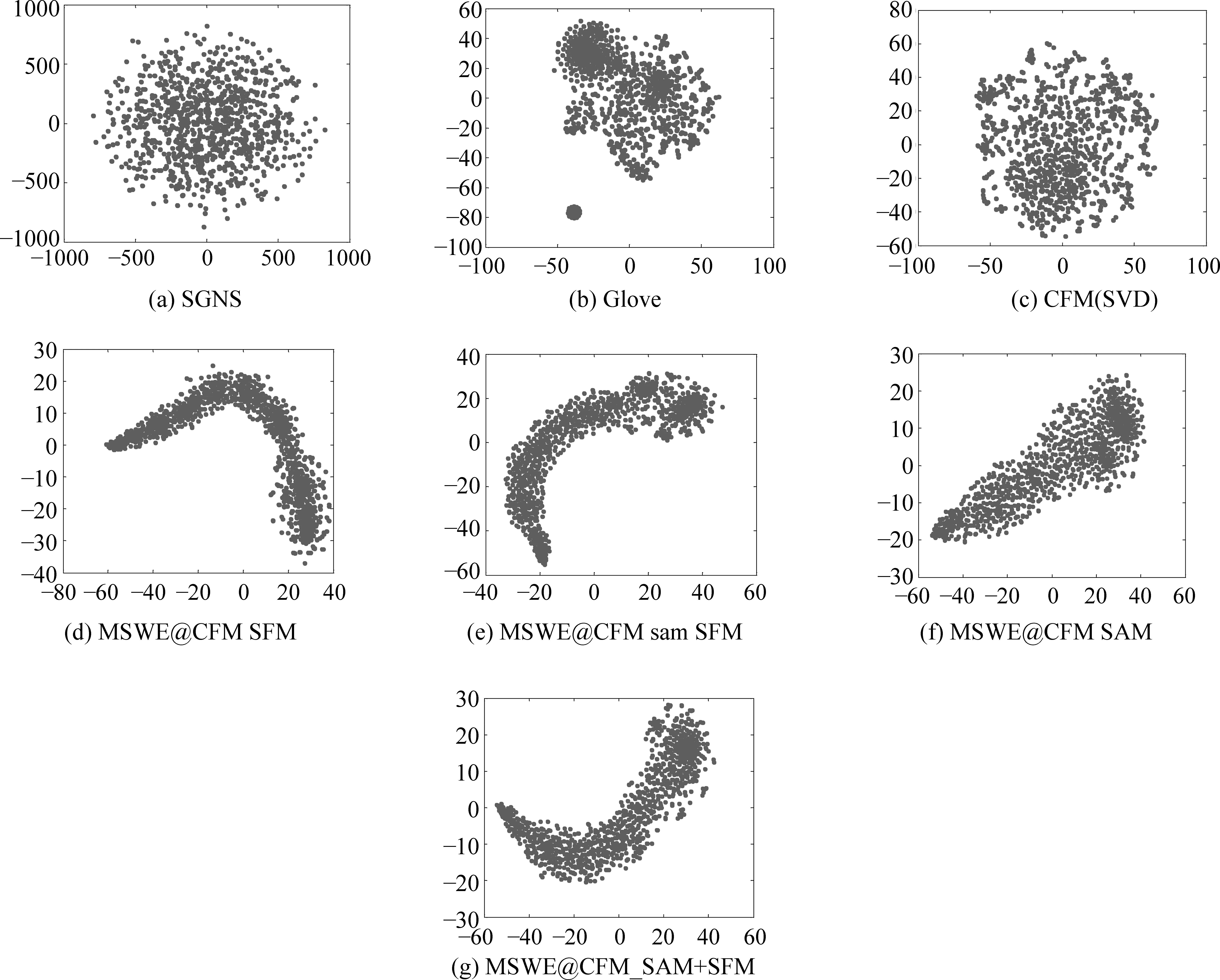
图3 词表示向量可视化
从图3可以看出,SGNS和CFM(SVD)所训练得到的词表示经过降维可视化后呈现出较为凌乱的布局。Glove的可视化结果中表现出了两个明显的聚类现象。本文中所采用的MSWE@CFM_SFM、MSWE@CFM_sam_SFM、MSWE@CFM_SAM和MSWE@CFM_SAM+SFM的可视化结果为离散的线性分布趋势。经过分析可以发现,SGNS、Glove和CFM(SVD)三种算法仅仅考虑了词语的上下文结构关联。假如某些词语之间不存在上下文结构关系,则训练所得的词表示在向量空间上具有较远的距离,因此,投影到二维平面上就会呈现出离散的点布局。另外,本文基于词语的属性语义文本,可以从另外一个角度弥补因为词语上下文结构缺失导致的训练不充分问题。
在图3中(a)、(b)、(c)均为基于上下文结构特征的词表示学习算法获得的词向量可视化结果。从这三个可视化结果中可以发现,词表示向量的可视化分布显现出圆形的分布。因此,可以认为基于上下文结构训练所得的词向量在向量空间中的分布是均匀的。而图3中(d)、(e)、(f)、(g)为加入了同义词与反义词、属于语义文本后词向量的可视化结果,且呈现出离散的线性的分布。如果两个词语不互相出现于对方的上下文中,则基于结构训练所得的词表示的可视化中这两个词语的分布处于较远的距离较远。而如果这两个词语为同义词或具有相似的属性语义文本,则本文提出的MSWE算法能够使得这两个词语在向量空间中具有更近的空间距离。因此,同义词与属性语义文本犹如两种不同性质的力,使得这些离散而凌乱的点更加靠近。
4 总结
本文提出了一种基于多源信息融合的词表示学习算法(MSWE)。该算法从基于神经网络的词表示学习中获得灵感,引入了SGNS的矩阵分解形式矩阵(SPPMI矩阵)。研究了SPPMI矩阵和SGNS之间的关系,并探讨了如何构建SPPMI矩阵才能使其性能与基于神经网络的SGNS性能达到一致水平或更优。为了获得更加优异的词表示学习性能,本文引入了多视图集成学习的思想。该思想使用了多源的词特征组合优化学习,进而提升词表示学习的性能。本文引入了词的同义词和反义词数据、词语的语义文本数据来优化词向量学习模型,即优化本文提出的基于神经网络的词表示学习存在的3个不足。为了更好地从多源数据中学习到有价值的数据特征,本文引入了诱导矩阵补全算法。实验结果表明,诱导矩阵补全算法能够显著地提升词表示学习的性能,其性能优于简单地将多源特征进行拼接的方法。MSWE的性能在Rare Words和M.Turk词语相似度评测数据集上提升是最明显的,在其余4个词语相似度评测数据集上也均有明显的性能提升。本文在随后的实验章节,又着重分析了MSWE算法的参数影响,得到了一些有价值的参数组合,例如,MSWE在向量长度为30时的词表示性能优于长度为100的词表示。尤其是在可视化小节中发现,MSWE算法训练得到的词表示在二维平面上呈现出离散的线性分布趋势。该发现证明本文提出的MSWE算法使得更相关的词语在向量空间上具有更近的空间距离,而非相关词语在向量空间上具有更远的空间距离,其实质也是对SGNS的一种向量优化。
