高中数学核心素养引领下的课堂发散思维训练研究
2019-10-21柴有茂

【摘 要】现在所指的数学核心素养包括数学抽象、逻辑推理、数学建模、数学运算、直观想象和数据分析,是数学核心知识和核心能力的表现。数学教学中不断进行发散思维的训练则是培养学生创新能力、提高数学思维能力和优化思维品质的重要措施和主要途径。本文就如何在高中数学核心素养的引领下展开课堂发散思维的训练进行研究与实验。
【关键词】核心素养;数学课堂;发散思维
一、核心素养概述
对于高中数学学科而言,核心素养主要涉及数学抽象思维、逻辑推理、数学建模、数学运算、直观想象和数据分析等能力。核心素养的提出,要求学生在数学学习过程中,个人具有对数学在现实世界中所起的作用有自己的理解,个人可以对数学作出合理的解释以及有理有据的分析;通过计算、测量、分析等多种方式加深对数学的理解,从而形成数学思维和数学习惯;除此之外还要思考用什么样的思维方式解决数学问题,用什么样的思维方法探究问题。而教学实践表明数学教学中不断进行发散思维的训练则是培养学生创新能力,提高数学思维能力的主要途径。
二、发散思维概述
发散思维是一种多角度思考问题、多途径解决问题的思维方式,要求学生能够举一反三,触类旁通。因此在高中数学教学中正确培养学生的发散思维能力,对造就创新人才,强化学生创新意识,提高其数学素质有着举足轻重的作用。
(一)通过一题多解,培养思维的流畅性
知识是思维的基础。学生在掌握了一定的基础知识、基本方法之后,对一些典型的数学问题,要选择不同的解题方向,采用不同的方法来解答,这样可以沟通各部分知识点的内在联系,达到举一反三的目的。
(二)通过广泛的联想,培养思维的变通性
联想是根据研究对象或问题的特点,联系已有的知识和经验进行想象的思维方法。在解决数学问题的过程中,针对数学问题的内容特点展开联想,从不同层次、不同侧面揭示事物的本质,可以排除思维定式的消极影响,使思维适应变化的条件,达到变通灵活的目的。
(三)通过大胆猜想,培养思维的独特性
猜想的形成是对所研究的对象或问题,通过联系已有的知识经验进行分析、选择、加工和改造的过程。数学猜想包括解题主导思维方法的猜想、结果的猜想以及对问题的整体猜想。数学猜想往往会使人产生独特的见解、新颖的方法和出人意料的结果。
三、组织实施
在教学的过程中,作为教师,必须首先具备培养学生发散性思维的意识,并在讲课的过程中慢慢渗透这一理念,让学生养成良好的思维习惯,培养自身的创新意识,促进学生的全面发展。为此我展开了为期两年的实验对比。
(一)实施方法
在太原十二中高一高二的班级中选择平行班,教师以不同的方式教学,进行成绩的比对。在教学过程中,例题的选择上注重一题多问、一题多解、一题多变的运用,引导学生从多角度、多方面去思考问题,寻求解决问题的途径,以这样培养学生的发散性思维。
(二)实施过程
第一階段 2015年9月~2016年7月
在高二年级选择理科1505班和文科1510班,分别由柴有茂和梁婷婷两位教师承担教学工作,进行为期一学年的教学实验,与同层次班级理科1506班和文科1509班比较成绩。
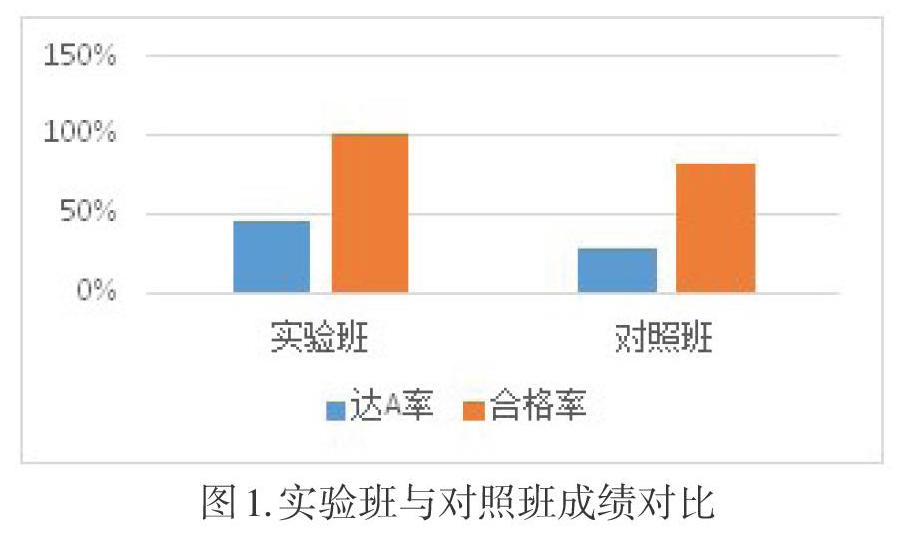
通过实验,平行的两个班差距不断增大,学生反馈,发散性思维学习增强了学习数学的信心和动力,尤其是文科1510班学生对数学学习更有兴趣,也更愿意在数学学科上分配更多的时间和精力。在高二会考中,理科1505班的达A率为45%,明显高于1506班的28%;文科1510班的合格率为100%,也明显优于1509班的82%(如图1)。
第二阶段 2016年9月~2018年6月
在高一年级选择1611班和1616班,分别由王建军和王瑞琦两位教师承担教学工作,进行为期两学年的教学实验,与同层次班级1612班和1615班比较成绩。
高一的教师注重让学生体会从不同角度看问题、一道题目变形引申不同问题等等。尤其在三角函数部分,学生试图一题多解,大胆猜想、勇于论证。随后学习了向量知识,与三角函数知识的衔接,又凸显了发散思维的必要性。在学习必修五的数列知识时,学生们在解题时不断迸发出来新鲜的解题思路,使发散思维的流畅性、变通性得到了提升。面对同一问题,学生想出的不同类型的答案不断增多,慢慢适应了这种遇到问题寻找多种途径解决的思维习惯。
到了高二文理分科,四个班级学生稍有变动,1611、1612班为理科班,1616、1615班为文科班。王建军和王瑞琦两位教师继续在1611和1616班进行教学实验。有了高一一年的基础,班级内大部分同学都能很快适应教师的教学方式,发散思维的流畅性和变通性的体现愈发明显。在高二后期的会考复习中,由于知识的连续性、系统性更强,学生们在面对同一问题时提出的思路更多、更清晰、更灵活,并且个别学生在思考问题时也凸显出自己的独特思维,想出不同寻常的新奇思路。
经过两年的教学实验,学生们的发散思维得以充分发展,同时学生的基础知识、基本技能得到提升,也增强了学生的运算能力、数学思维能力、数学语言表达能力、创新意识等等,拓宽了学生的视野。
在高一入校时1611和1616班的班均分稍逊于1612和1615班,分别相差2.1分和1.8。但是通过高一一年的教学实验,学生们学习数学的热忱不断增强,并体现在学习成绩上,在高一期末考试中,1611班的班均分比1612班高出3.6分,1616班的班均分比1615班高出3.9分。经历高二一年的继续培养,在高二第一学期末考试中,理科1611班的达A率为40%,明显高于1612班的23%,文科1616班的合格率为82%,也明显优于1615班的65%。同时在高二模拟会考成绩中,理科1611班的达A率为75%,明显高于1612班的52%;文科1616班的达A率为20%,也明显优于1615班的达A率8%。
四、下一步探讨的问题
1.在一题多解的过程中,如何使学生思路顺畅,保持思维的流畅性。2.注重从实际出发,从学生的角度理解问题,从而更好地选择发散点及发散方式。3.在课堂教学中,如何把教师主导地位与训练学生发散思维有机地结合起来,使学生不拘泥于教师的思路,思维发散更加合理、高效。核心素养对高中数学教学的冲击,绝对不只是简单的一个新概念的引入,而是要重新建立对数学教学的理解。作为教师,必须首先具备培养学生发散性思维的意识,并在讲课的过程中慢慢渗透这一理念,始终把培养学生的发散性思维放在最重要的位置,让学生在学习数学知识的同时,可以养成良好的思维习惯,培养自身的创新意识,促进学生的全面发展。
参考文献:
[1]于波.基于核心素养视域下的高中数学课堂教学[J].教育,2017(2).
(责任编辑 范娱艳)
