含多条裂纹变截面简支梁的自由振动

马一江， 李园园， 陈国平， 赵颖杰

(1. 江苏科技大学 船舶与海洋工程学院， 镇江 212003; 2. 南京航空航天大学 航空宇航学院， 南京 210016； 3. 济南大学 机械工程学院， 济南 250022)

在工程实际中，像航空航天工业、船舶工业以及建筑桥梁等，梁结构的应用变得越来越广泛，包括等截面梁、变截面梁等。随着科学技术的快速发展，变截面梁的设计与加工工艺更加成熟，为变截面梁的广泛应用提供了可能。与等截面梁相比，变截面梁具有更好地承力性能和振动特性。在梁结构的动力学特性分析中，等截面梁的自由振动问题较为简单，而变截面梁的控制方程为四阶变系数偏微分方程，通常情况下很难得到解析解[1-3]。

关于变截面梁模态分析的早期研究中，通常将整个变截面梁分段离散成多段变截面梁，并将每段变截面梁等效简化为等截面梁。阶梯梁是变截面梁中最简单的一种，也是最早应用离散方法进行模态分析的变截面梁[4-6]。对于普通的变截面梁结构，为了提高计算精度，通常将变截面梁离散的非常多，使得模态分析的计算量成倍增加。在每段变截面梁简化为等截面的过程中，学者们提出了很多等效方法来提高计算精度[7-8]。同时学者们也提出了许多其他方法来研究变截面梁的模态变化。 Gupta[9]采用有限元方法求解变截面梁结构的各阶固有频率。Alshorbagy等[10]通过数值有限元方法研究了功能梯度变截面梁的动力学特性。Huang等[11]将轴向梯度非均匀梁的振动微分方程转化为积分方程，提出了一种研究轴向梯度非均匀梁自由振动的分析方法。Ahmad等[12]基于微分变换法提出了一种微分变换单元法来研究锥形变截面梁的自由振动和稳定性。Mehmet等[13]通过理论方法研究了截面宽度沿指数变化的矩形变截面梁的振动特性。Laura等[14]采用近似数值方法研究宽度不变-厚度双线性变化的变截面梁固有频率和固有模态的变化。Caruntu[15]研究了宽度不变-厚度抛物线变化变截面梁的非线性振动问题。上述文献研究了不同形式变截面梁的模态变化，为变截面梁的工程应用提供了理论依据，但是忽略了结构损伤对变截面梁的影响。

由于加工和装配等原因，服役中的梁结构多多少少会存在初始结构损伤。梁结构上的结构损伤通常以裂纹的形式出现，裂纹的存在会严重影响梁结构的振动特性，并且显著降低梁结构的振动疲劳寿命。因此，对含裂纹梁结构进行模态分析具有非常高的工程应用价值。Ostachowicz等[16-17]将横向裂纹等效为梁结构的断点，研究含多条横向裂纹梁结构的模态响应，并通过模态的变化探测结构损伤的位置和尺寸。Shifrin等[18]提出一种传递矩阵方法来求解含多条裂纹等截面梁的固有频率，这种传递矩阵方法使得含裂纹梁结构传递矩阵的阶数始终为4，显著降低了含多条裂纹梁模态分析的计算量，提高了计算效率。但是这些研究仅限于等截面梁结构，并没有考虑梁结构变截面参数的影响。随着变截面梁的广泛应用，含裂纹变截面梁的模态分析成为工程中亟待解决的问题。

本文提出一种计算含多条横向裂纹变截面矩形梁固有频率的新方法。针对高度不变-厚度指数变化的一类变截面梁，将每个横向裂纹看作是变截面梁的断点，则整段变截面梁离散为多段变截面梁。基于传递矩阵法和Euler-Bernoulli梁理论，推导出每段变截面梁的传递矩阵；根据裂纹左右两面的连续性条件，推导出每条裂纹的传递矩阵；从而得到含多条横向裂纹变截面梁的传递矩阵。结合简支梁的边界条件，求解含多条裂纹变截面简支梁的固有频率。

1 模型建立

如图1所示，本文的研究对象是一个含n条横向裂纹的矩形变截面梁结构，梁的长度为L，每个横截面(沿着x轴方向)的厚度和高度分别为b(x)、h(x)。每条横向裂纹的位置分别为X1,X2,…,Xn，每条横向裂纹的深度为a1,a2,…,an。

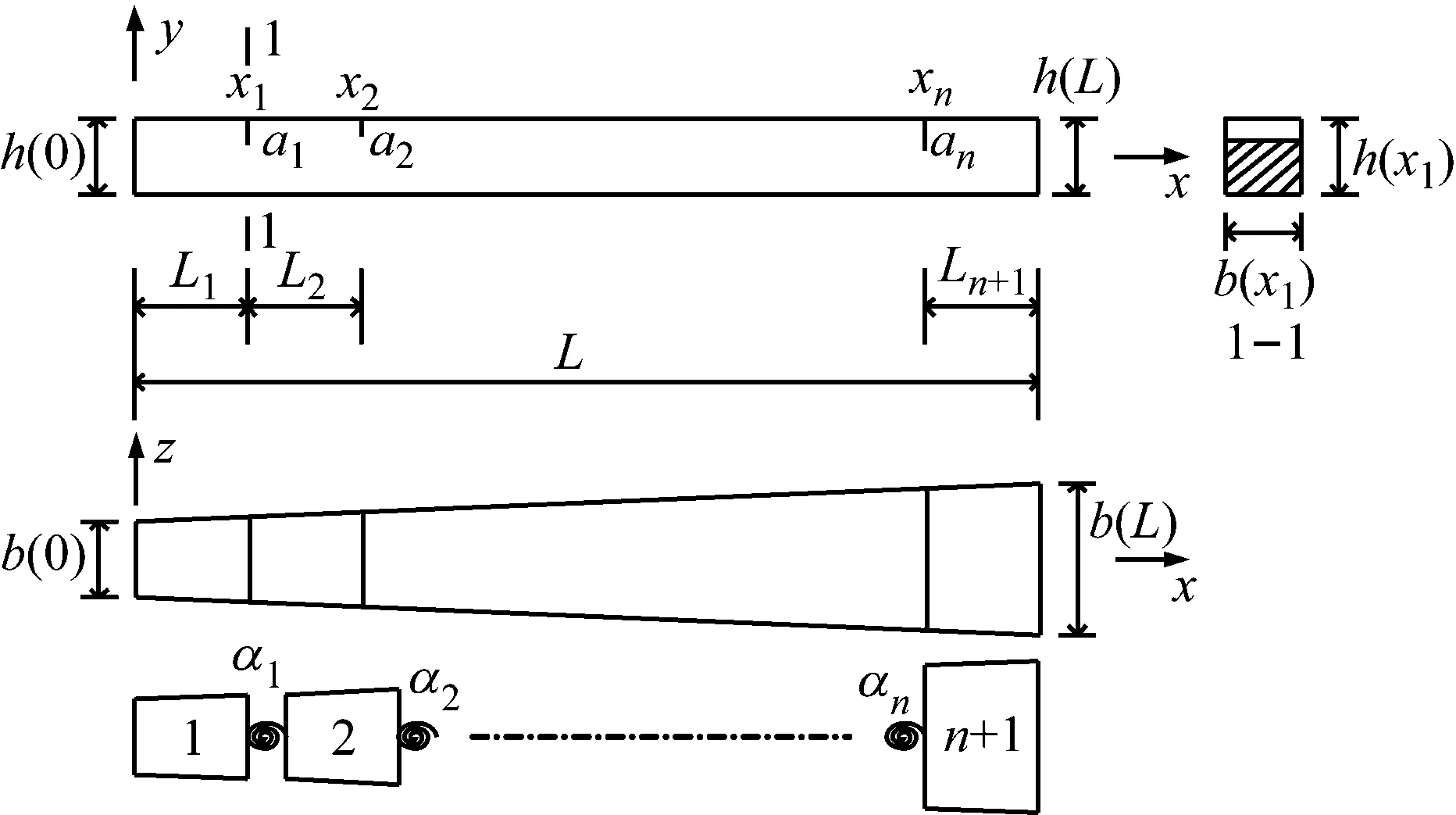
图1 含多条裂纹变截面梁的模型

根据Dimaronas等[19]提出的裂纹局部柔度模型，每条横向裂纹在变截面梁上引起的局部柔度变化可以表示为

(1)

式中：裂纹的编号i=1,2,…,n；αi为第i条横向裂纹引起的变截面梁局部柔度；h(x)为第i条横向裂纹所在的变截面梁横截面高度；I(x)为第i条横向裂纹所在的变截面梁横截面惯性矩；ri=ai/h(x)为第i条横向裂纹的相对深度；f(ri)为第i条横向裂纹的无量纲局部柔度函数，可以通过应变能密度函数来求解

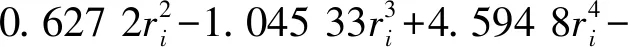
(2)

式中：ri≤0.6。

将每段横向裂纹看作是整个变截面梁的断点，则整段变截面梁被n条横向裂纹分为n+1段完整的变截面梁，并且每段变截面梁的长度为Li(i=1,2,…,n+1)。根据Euler-Bernoulli梁理论，每段变截面梁的振动微分方程可以表示为

(3)

式中：E为变截面梁结构材料的弹性模量；A(x)和I(x)为每段变截面梁横截面的面积和惯性矩；ρ为变截面梁结构材料的密度。

根据Mehmet等给出的无量纲方法，在图2所示的坐标系中，定义如下的无量纲化变量

(4)

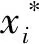
(5)

根据模态分析方法，式(5)为四阶变系数线性齐次微分方程，可以通过分离变量法求解。假设每段完整变截面梁具有如下的横向振动形式

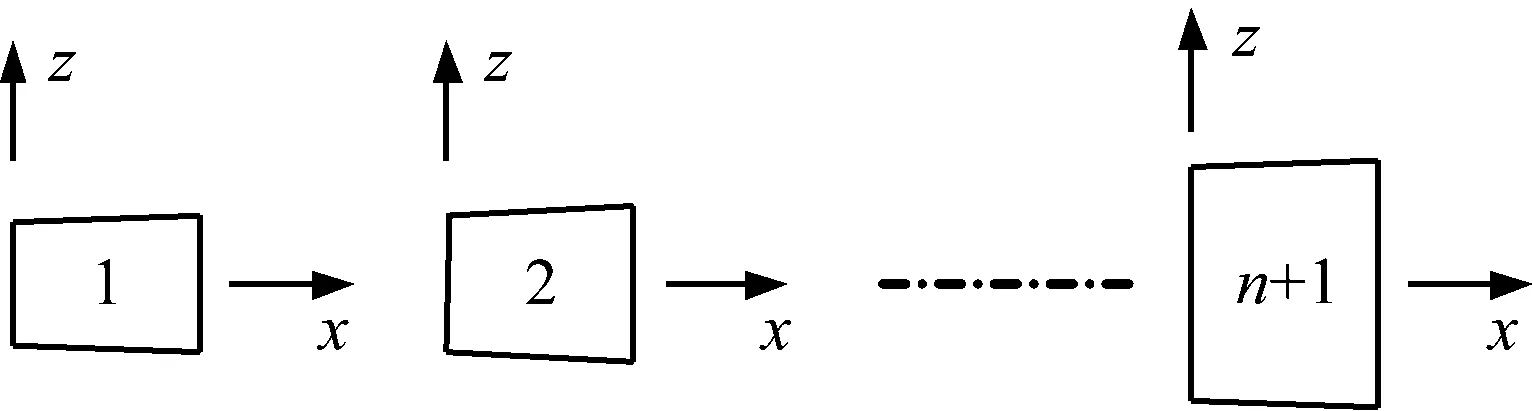
图2 每段变截面梁的模型

wi(xi,t)=Ui(xi)qi(t)

(6)

将式(6)代入式(5)，可以推导出以下方程组

(7)

(8)

式中：ω为无量纲固有频率，且ω2=Ω2ρL4/EI1,0;Ω为固有频率。

经过推导，式(8)的解为

qi(t)=Ci1cos(ωt)+Ci2sin(ωt)

(9)

在变截面梁振型函数的求解过程中，需要变截面梁的变截面参数。以高度不变-厚度按指数形式变化的矩形变截面梁为例，即h(x)=h。根据图2所示的坐标系，假设该变截面梁每段变截面梁横截面的面积为Ai(xi)=eδxi+κi、惯性矩为Ii(xi)=eδxi+κi。其中，δ为矩形变截面梁的变截面参数；κi为该矩形变截面梁的厚度参数，且κi=δ(L1+L2++Li-1)/L。

对于横截面高度不变-厚度按指数变化的一类变截面梁结构，式(7)可以简化为

(10)

则式(10)的解可以表示为

(11)

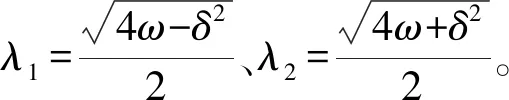
2 传递矩阵推导

根据材料力学的理论，梁结构横截面连续性参数如下：挠度U、转角θ、弯矩M以及剪力Q，每个连续参数的求解公式为

(12)

在每段变截面梁的左端横截面，4个连续性参数可以表示为

Ui(0)=Bi1+Bi3

将以上方程组转化为矩阵形式为

(13)

式中：

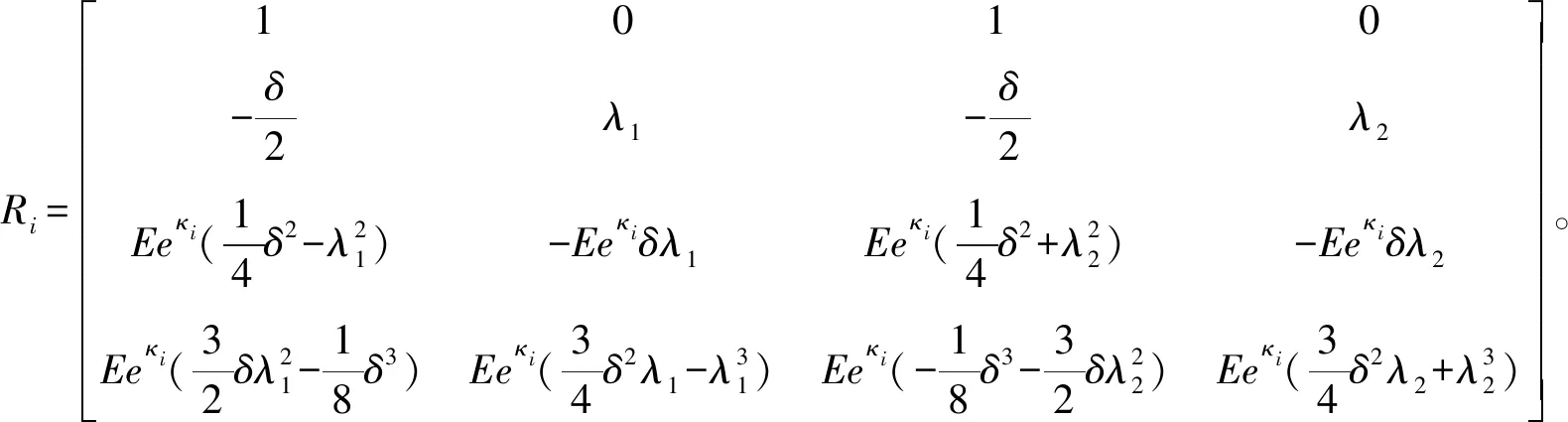
在每段变截面梁的右端横截面，4个连续性参数可以表示为

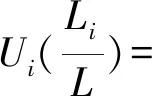
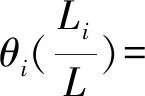
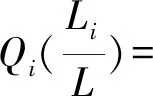
将以上方程组转化为矩阵形式

(14)

将式(13)代入式(14)，可以得到每段变截面梁结构左右端横截面连续性参数的关系式

(15)

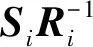
在每个横向裂纹位置，根据裂纹左右表面的连续性条件，可以得到裂纹左右表面的挠度、转角、弯矩以及剪力的关系式

(16)

对于含有n条横向裂纹的矩形变截面梁结构，左右两端挠度、转角、弯矩和剪力的关系式如下

(17)

根据简支梁的边界条件，简支梁左右两端横截面的挠度和弯矩为零

(18)

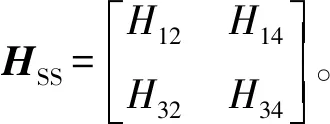
detHSS=0

(19)

式(19)可以求解含裂纹变截面简支梁的各阶固有频率，且每阶固有频率对应的固有振型可以通过式(11)推导出来。

3 结果与讨论

如图1所示，假设该含多条横向裂纹矩形变截面简支梁的几何尺寸为：L=1 m，h=0.06 m，b(x)=0.06eδxm。该变截面梁结构材料为低碳合金钢AISI 1050，且材料力学参数为：E=210 GPa，ρ=7 860 kg/m3。

定义ωi为梁结构变截面参数δ对应的变截面梁第i阶固有频率；当梁结构的变截面参数δ=0时，定义ωi0为变截面梁的第i阶固有频率；定义变截面梁固有频率比Γi=ωi/ωi0。假设该变截面简支梁不含有横向裂纹，随着变截面参数的变化该变截面简支梁各阶固有频率比的变化规律，如图3所示。

由图3可知，变截面简支梁的各阶固有频率比受变截面参数δ的影响非常大，并且图3与参考文献[13]几乎一样，因此本文提出的传递矩阵方法是正确的。随着梁结构变截面参数|δ|的逐渐增大，变截面简支梁的第一阶固有频率比逐渐减小，并且减小的速度逐渐增大。当变截面参数δ=0时，变截面简支梁第一阶固有频率最大。随着梁结构变截面参数|δ|的逐渐增大，其他四阶固有频率比均逐渐增大，并且增大的速度也逐渐增大。当变截面参数δ=0时，变截面简支梁其他四阶固有频率均最小。

图3 变截面参数不同时各阶固有频率比的变化规律

Fig.3 Each order natural frequency variation of the variable cross-section beam with different variable parameter

假设该变截面简支梁上仅含有一条横向裂纹，且变截面参数δ=-1；裂纹的相对位置为L1/L∈[0.11,0.89]，裂纹的相对深度为a1/h∈[0,0.6]。随着横向裂纹相对位置和相对深度的变化，该含裂纹变截面简支梁第一阶固有频率的变化规律，如图4所示。

图4 裂纹位置和深度不同时变截面简支梁第一阶固有频率的变化规律

Fig.4 First order natural frequency variation of the variable cross-section beam with different depths and positions of the cracks

从图4可知，裂纹相对位置和相对深度对变截面简支梁第一阶固有频率的影响非常大。随着裂纹相对深度的逐渐增大，变截面简支梁的第一阶固有频率逐渐减小，并且减小的速度逐渐增大。当横向裂纹处于变截面简支梁左右两端截面时，裂纹对第一阶固有频率的影响可以忽略不计；随着横向裂纹逐渐靠近简支梁的中间横截面，变截面简支梁的第一阶固有频率也逐渐减小。

假设该变截面简支梁含有以下4种裂纹情况：

(1) 该变截面简支梁不含有横向裂纹。

(2) 该变截面简支梁含有一条横向裂纹，并且该横向裂纹的几何尺寸如下：X1=0.11 m，a1/h=0.1。

(3) 该变截面简支梁含有两条横向裂纹，并且横向裂纹的几何尺寸如下：X1=0.11 m，a1/h=0.1；X2=0.3 m，a2/h=0.1。

(4) 该变截面简支梁含有三条横向裂纹，并且横向裂纹的几何尺寸如下：X1=0.11 m，a1/h=0.1；X2=0.3 m，a2/h=0.1；X3=0.5 m，a3/h=0.1。

若该变截面简支梁的变截面参数δ=0.5，则不同的裂纹情况对应的含裂纹变截面简支梁前五阶固有频率，如表1所示。

表1 裂纹条数不同时变截面简支梁的前五阶固有频率

Tab.1 First five orders natural frequencies of the variable cross-section beam with different number of cracks

rad/s

从表1可知，结构裂纹的存在对变截面简支梁前五阶固有频率的影响都很大，因此结构裂纹对变截面梁结构的破坏是不能忽略的。随着裂纹条数的逐渐增多，变截面简支梁的每一阶固有频率均逐渐减小。

如果仅考虑变截面简支梁的第一阶固有频率变化，假设变截面简支梁存在以下三种裂纹情况：

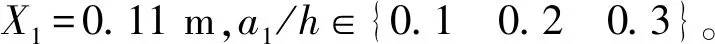
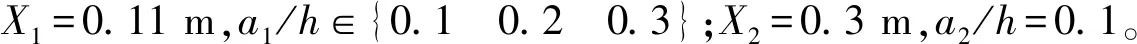
若该变截面简支梁的变截面参数δ=0.5，则不同的裂纹情况对应的含裂纹变截面简支梁第一阶固有频率，如表2所示。

表2 不同裂纹情况变截面简支梁的第一阶固有频率

Tab.2 First order natural frequency of the variable cross-section beam with different cracks

rad/s

从表2可知，第一条横向裂纹的相对深度对变截面简支梁第一阶固有频率的影响很大。随着第一条横向裂纹的相对深度逐渐增大，含裂纹变截面简支梁的第一阶固有频率逐渐减小；随着横向裂纹条数的逐渐增多，含裂纹变截面简支梁的第一阶固有频率也逐渐减小。

4 结 论

(1) 提出了一种求解含多条裂纹变截面简支梁固有频率的理论方法。根据横向裂纹条数，将变截面梁结构离散成多段完整的变截面梁。

(2) 基于传递矩阵方法，分别推导出每段完整变截面梁和每段横向裂纹左右表面的传递矩阵，得到含裂纹条数、裂纹几何参数以及变截面参数的整段变截面梁的传递矩阵；根据简支梁的边界条件，推导出变截面简支梁的特征传递矩阵，并计算出含多条横向裂纹变截面简支梁的各阶固有频率。

(3) 针对高度不变-厚度按指数变化的一类变截面梁结构，本文提出的理论方法能够准确、有效地求解含任意条数横向裂纹变截面的固有频率，并且本文的方法还适用于悬臂梁、双边固支梁等一系列不同的边界条件，同时不需要推导出固有频率的解析解，大大提高了计算效率。