基于改进Rayleigh-Ritz法的复杂形状平面薄板自振特性分析
2019-10-21李天匀郭文杰
张 俊, 李天匀, 朱 翔, 郭文杰
(1.华中科技大学 船舶与海洋工程学院,武汉 430074; 2.船舶与海洋水动力湖北省重点实验室,武汉 430074;3.高新船舶与深海开发装备协同创新中心,上海 200240; 4.华东交通大学 铁路环境振动与噪声教育部工程研究中心,南昌 330013)
板壳结构广泛用于工程领域中,薄板振动分析的解析方法,大多只能针对简单形状,然而实际问题却非常复杂,因此对复杂形状板的振动问题进行研究具有重要意义。
对任意形状问题求解主要采用数值方法,如有限元方法、微分求积法、边界点法等。数值方法以其天然的优势较为容易地应用于求解任意形状结构问题,但同时也存在一些劣势。比如划分网格依赖使用者的经验,在计算精度分析上需要耗费精力;模型参数有变动时需重新建模,比较费时费力。
解析方法作为一种简单有效的分析方法,已经广泛地应用于简单板壳问题的静动态分析。焦映厚等[1]采用了波动法研究有限尺寸加肋L型板结构的振动特性。杨念等[2]应用解析方法研究了含复杂结构应力的平板振动问题。Rayleigh-Ritz法作为一种常见的解析方法,得到广泛的应用。李正良等[3]基于Rayleigh-Ritz法分析了正交加筋圆柱壳-球壳组合结构的自振特性。邱永康等[4]应用Rayleigh-Ritz法,对任意边界条件下中心开口矩形板的自振特性进行分析。李凯等[5]结合Rayleigh-Ritz法计算了开口矩形板的固有频率和振型。解析方法具有较多的优势,能够从理论上揭示结构振动特性,便于机理分析,可以用于检验数值方法等。然而对于复杂形状的平板,试函数很难得到,公式推导非常复杂等,传统Rayleigh-Ritz法等解析方法难以解决复杂形状板壳振动问题。
解析方法要实现对复杂形状问题的求解,对其带来的曲边的边界条件问题的处理尤为关键。虚拟弹簧模拟边界条件作为一种灵活的方法被广泛采用[6-9]。Li[10]应用解析法分析了矩形板的面内振动,将位移弹簧和转角弹簧取相应的刚度值来模拟边界条件。但是以上研究多是处理直边边界,对弹簧模拟曲边的边界条件的研究还较少。
在Rayleigh-Ritz法的基础上,本文提出了一种用于求解复杂形状板振动问题的半解析方法——改进的Rayleigh-Ritz法。传统的Rayleigh-Ritz法及目前提出的一些计算特定形状平板振动的方法适应性不太好,且很多形状无法找到合适的试函数。本文方法适用于计算复杂形状平板振动问题,在不重新建模的情况下,可以对各种复杂的边界条件进行计算,具有很高的效率和适应性。方法主要改进在:一是拓展试函数域,使模拟复杂形状结构的位移函数易得;二是结合弹簧边界方法,用于处理复杂形状结构的边界条件,尤其是分析曲形边界。与传统Rayleigh-Ritz法相比,本方法的应用范围更广,精度也较高,为工程问题中复杂形状板的振动问题的求解提供了参考。
1 改进的Rayleigh-Ritz法
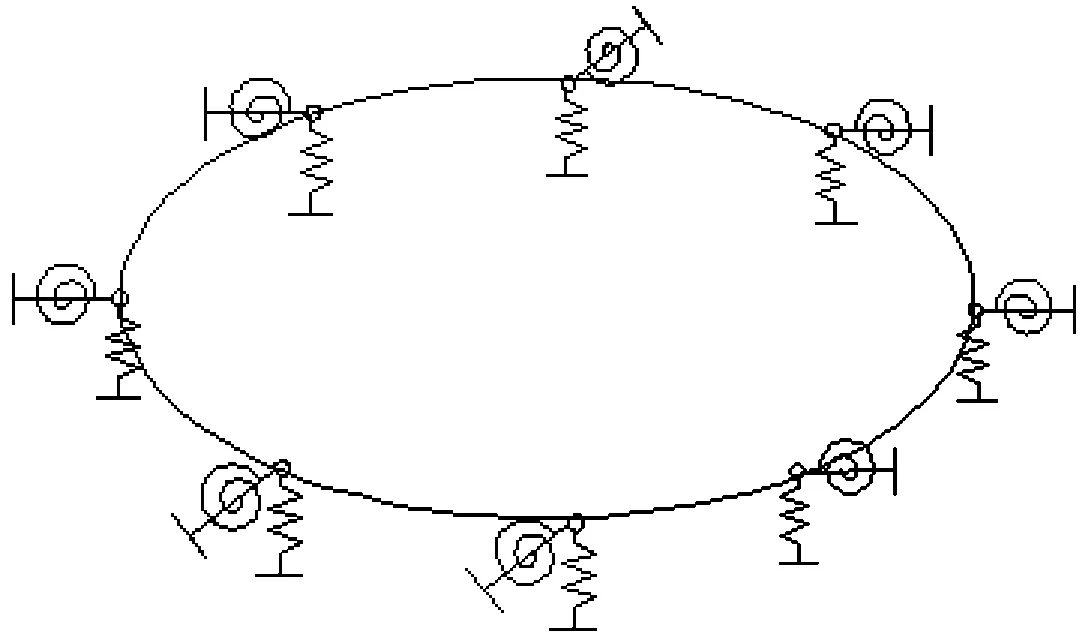
复杂形状板物理模型如图1所示:板面为S,沿边界分布着位移线弹簧和转角线弹簧,两种弹簧的刚度系数分别为k和K。
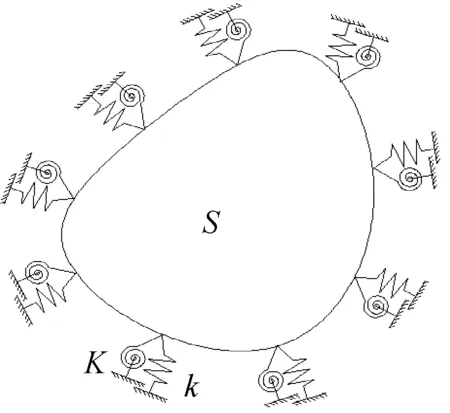
图1 复杂形状薄板的物理模型
1.1 方法的主要特点
1.1.1 函数域的拓展
对Rayleigh-Ritz法中的函数域进行扩展,模型如图2所示。
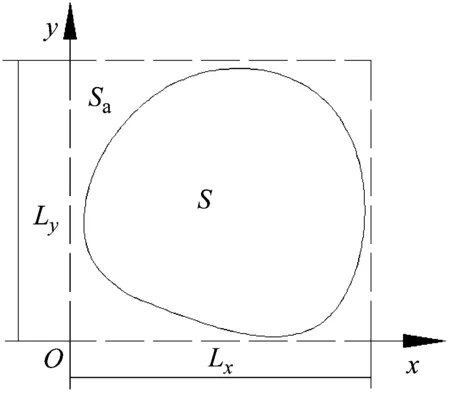
图2 复杂形状板的计算模型
S为薄板的求解域,Sa为试函数的积分域,长度分别为Lx和Ly。由于矩形区域的试函数易于表达,当求解域是不规则形状时,可以假想将结构域扩展为一个略大于真实域的矩形域,矩形域要能够包含结构域,按照矩形域选取结构的试函数。计算时对结构域进行积分,得到板的应变能、动能等,结果非常准确。研究表明,函数域越接近结构域,得到的解越精确,这也是本方法选择函数域的一个原则。所以当矩形域刚好与不规则结构域外切时,得到的结果误差最小。
在求解应变能、动能时需对板的结构域积分,以半径为R的圆板为例,由于其对称性,计算积分时只计算其1/4的结构,弯曲应变能为
(1)
(2)
圆板的应变能和动能通过二重积分得到。通常情况下,不规则形状的边界可以用多项式拟合,可以通过积分计算其能量。
值得注意的是,有些复杂的函数很难直接积分,为了解决这个难题,同时也为了提高计算效率,本文引入离散方法计算积分,具体离散的方式如图3所示。
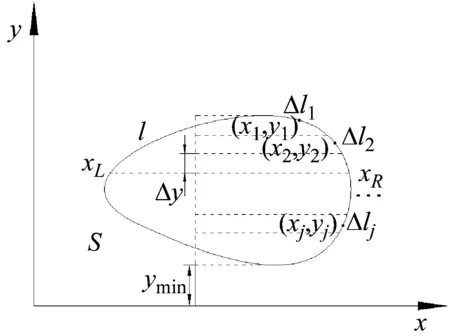
图3 沿纵坐标离散示意图
沿y方向将积分域分为Q等份,每份宽为Δy,纵坐标为yj,根据曲线的表达式计算出yj处对应积分域的长度Lxj,表示为:
Lxj=xR-xL
(3)
再将Lxj平均分为Q份,长度为
Δxj=Lxj/Q
(4)
离散后小分段的横纵坐标分别为
xij=Lxj+(i-0.5)·Δxj
(5a)
yj=ymin+(i-0.5)·Δy
(5b)
则二重积分可以转化为对微面积的求和,应变能与动能都可以表示为如下形式
(6)
式中:C为系数;f(xij,yi)为计算应变能与动能时的相关的函数。
这样大大提高了计算效率,并解决了部分函数难以直接积分计算的难题。
1.1.2 虚拟弹簧处理曲形边界条件
经典边界条件,如固支和简支等往往不能准确模拟实际结构的边界,考虑一般性,采用弹簧模型模拟边界条件。在结构域的边界上采用位移线弹簧和转角线弹簧。
假设位移线弹簧和转角线弹簧刚度值分别为kij(N/m2)和Kij(N/rad),复杂边界条件可通过调节弹簧的刚度值模拟。经典边界条件的刚度取值如表1所示。模拟弹性边界条件时则将刚度系数取为相应的值。

表1 经典边界条件下的弹簧取值
对于本文所研究的复杂形状板,其边界为曲形边界,则弹簧的弹性势能表示为
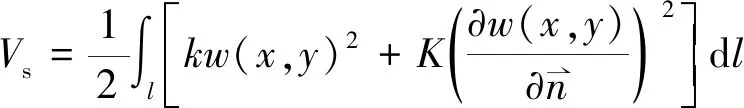
(7)
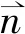
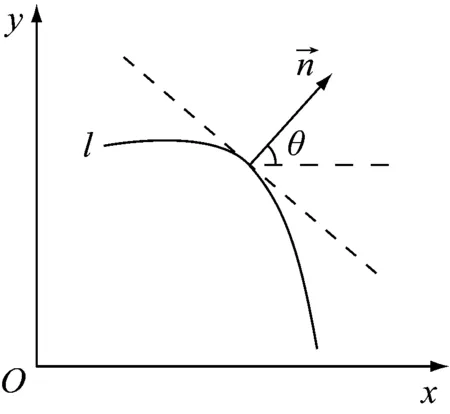
图4 边界处偏导数计算示意图
其中曲边对法线方向的偏导数表示为
(8)
对边界做离散处理,如图5所示。
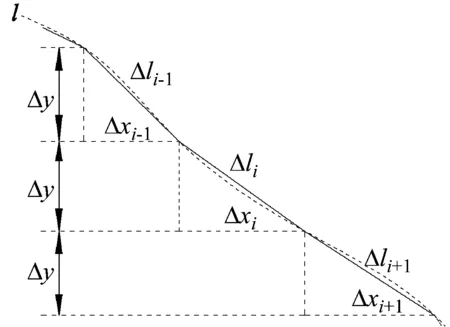
图5 边界处离散示意图
每个微段的长度为
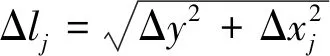
(9)
则边界处弹性势能可以表示为

(10)
1.2 分析过程
薄板的位移函数可以表示为
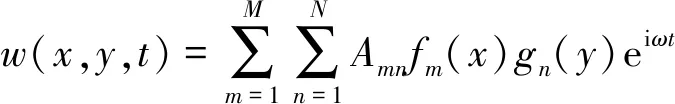
(11)
式中:Amn为未知的展开系数;m和n为序号;M和N为截断项数;fm(x)和gn(y)为沿x和y方向的正交多项式,选用改进的傅里叶级数,eiωt为简谐时间因子。
应用本文方法时,选取合适的试函数至关重要。由于改进的傅里叶级数可以满足任意边界条件,使板的试函数在整个求解域内三阶导数连续且四阶导数各点均存在,有效地克服边界处可能出现的不连续现象,选用改进的傅里叶级数作为试函数[11],表示为
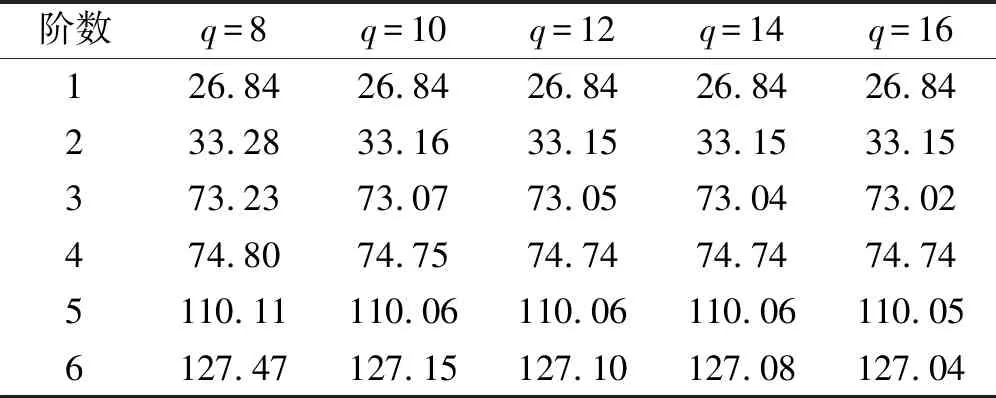
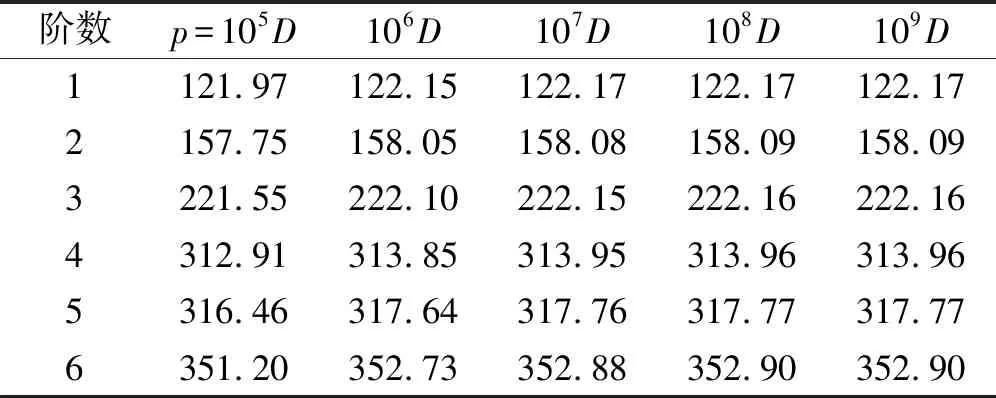
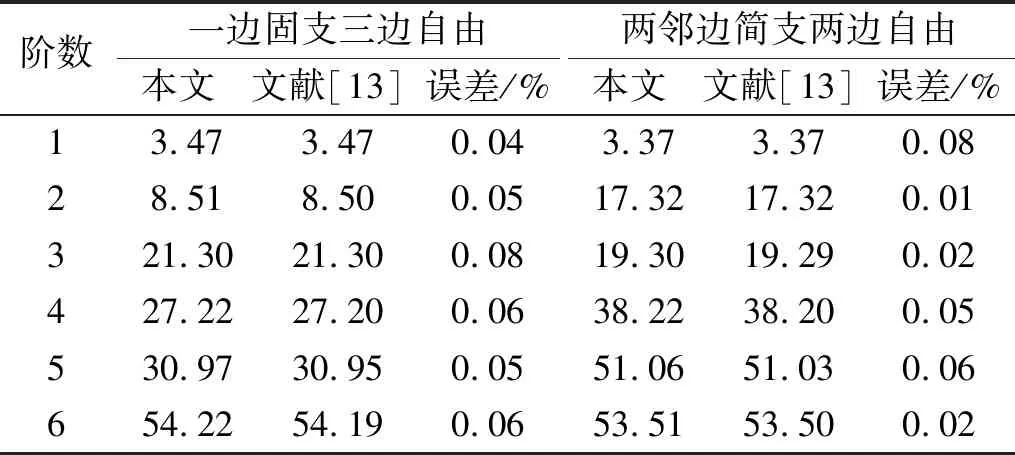
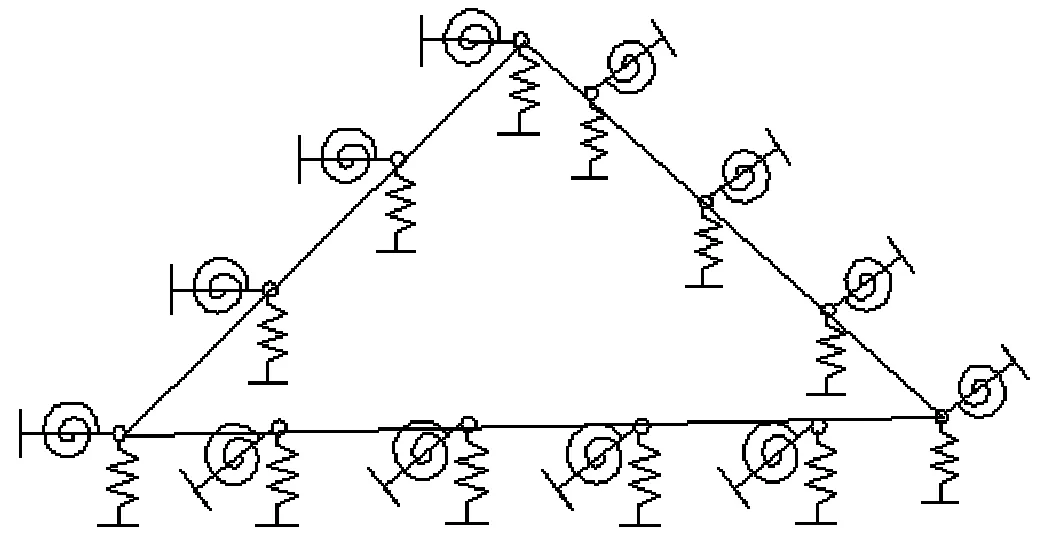
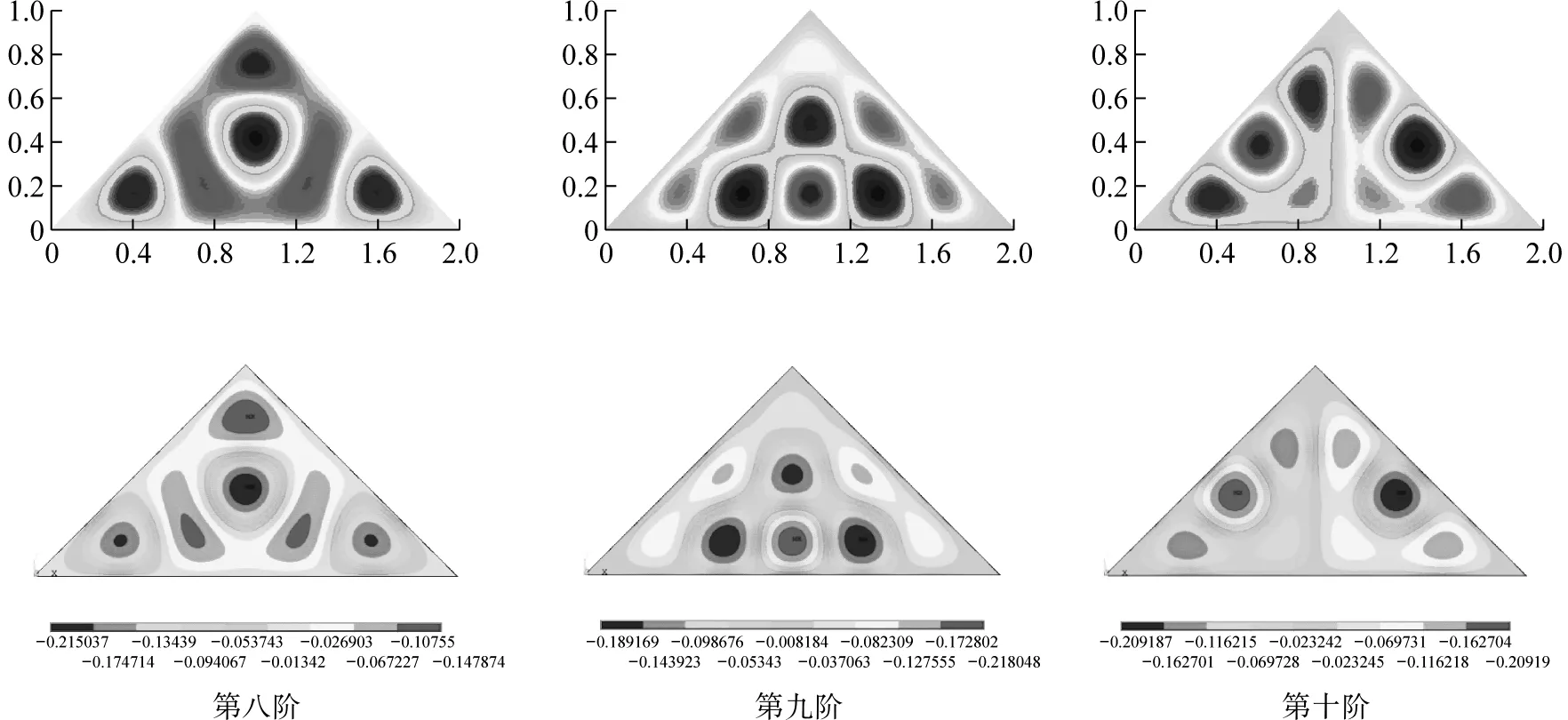
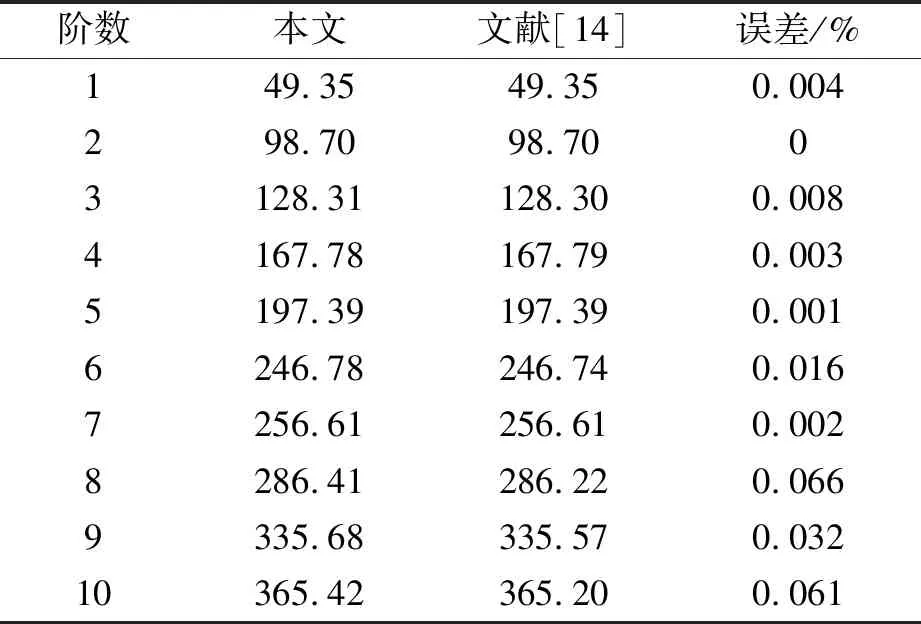
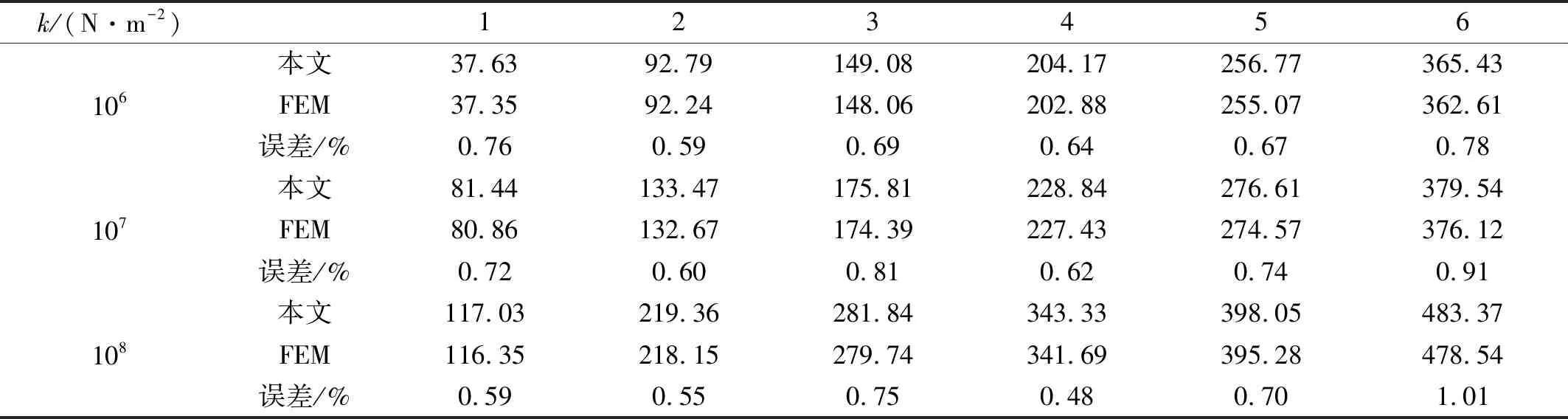
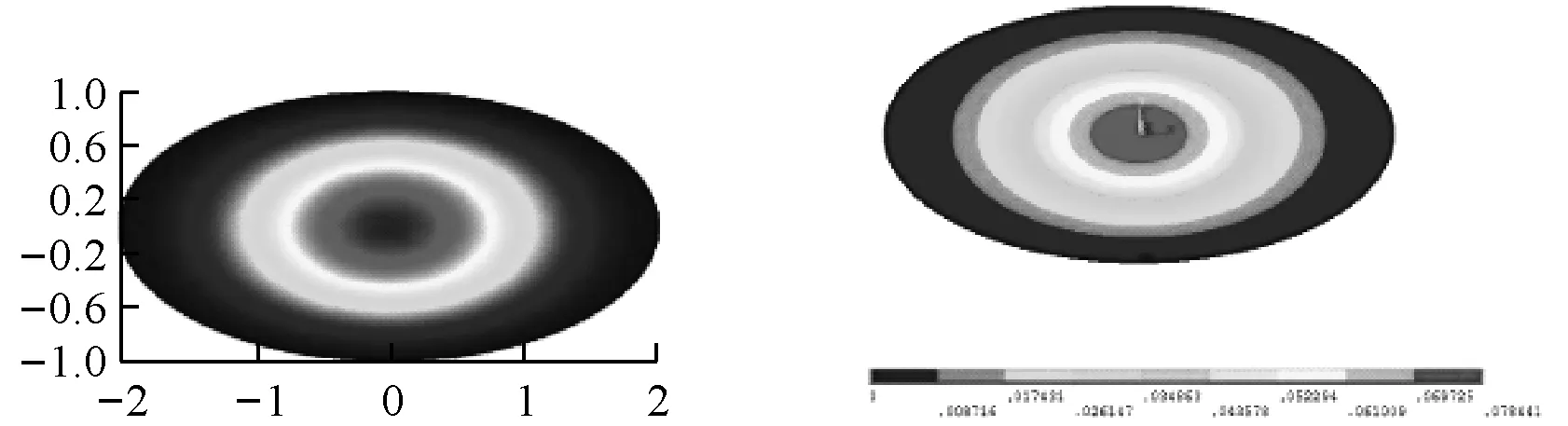
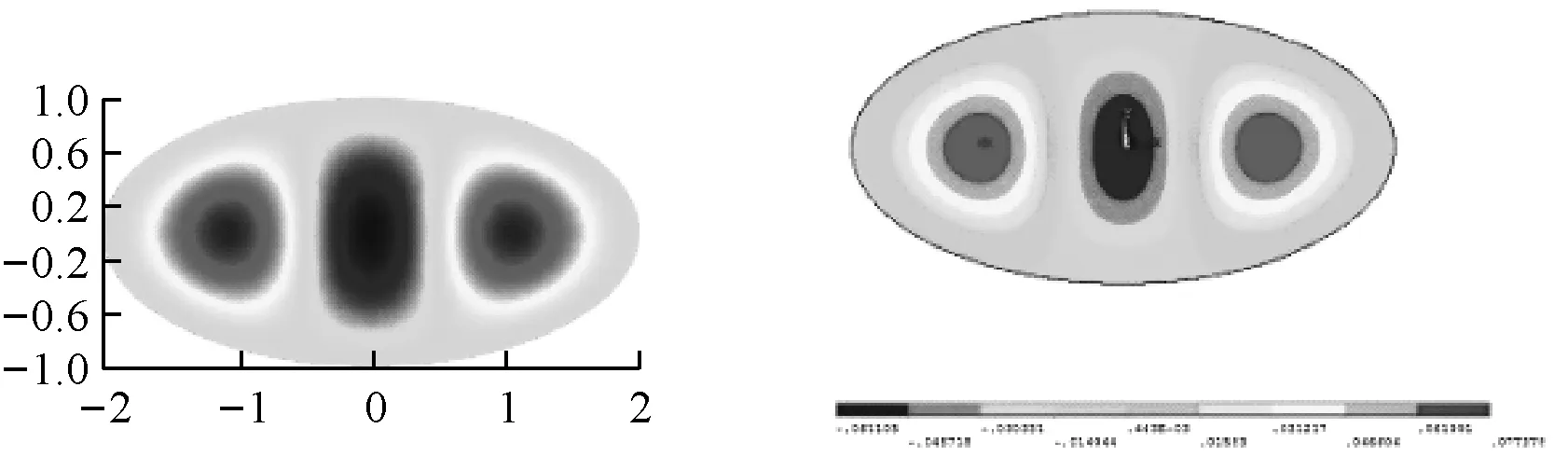
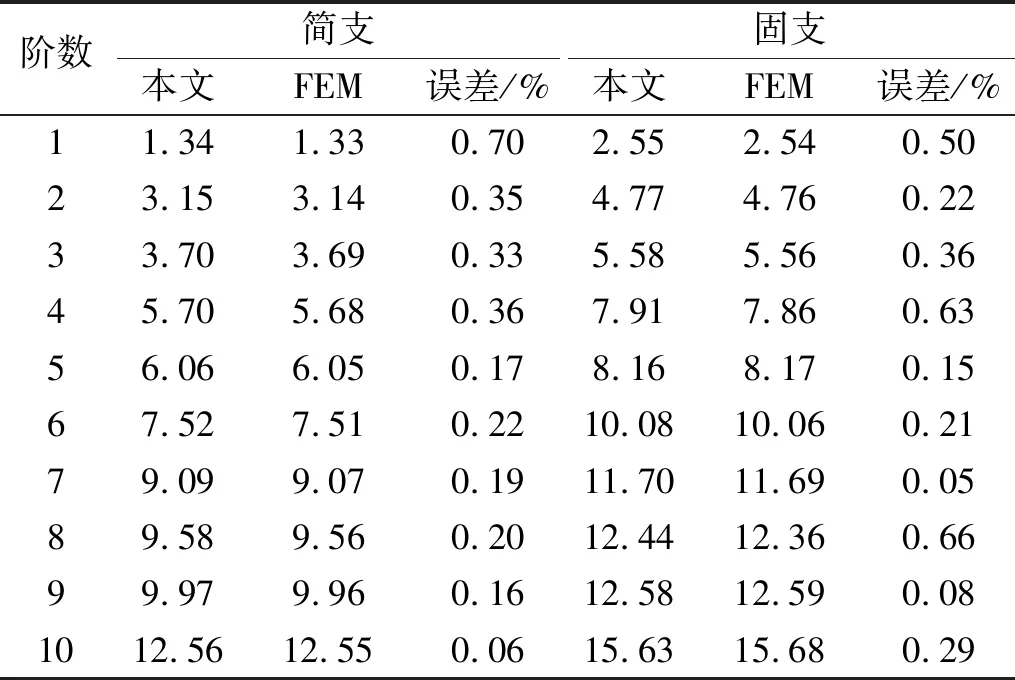
fm(x)=sin(mπx) 0 fm(x)=cos[(m-5)πx]m≥5 (12a) gn(x)=sin(nπx) 0 gn(x)=cos[(n-5)πx]n≥5 (12b) 式中:m=1,2,3,…,M;n=1,2,3,…,N。 为适用于计算复杂形状平板在多种边界条件下的振动问题,选择的试函数具有以下特点:是满足相应控制方程的正交函数;在边界处要具有任意性,即不能天然的满足某种几何边界条件。综上,还可以选用切比雪夫级数[12]等符合上述条件的具有任意性的函数作为试函数。 薄板的弯曲应变能可表示为 (13) 式中:w(x,y)为结构振动试函数;μ为泊松比,D=Eh3/(12(1-μ2))为薄板的弯曲刚度,h为板厚,时间项eiωt可以解耦并省略。 忽略边界弹簧的质量,结构的动能为 (14) 式中:ρ为质量密度。 系统的能量泛函可以表示为 ∏=Vp+Vs-T (15) 将式(7)、式(13)、式(14)代入式(15),并对未知系数求极值: (16) 式中:Amn是描述薄板弯曲振动的未知系数。 于是结构的振动问题转化成了求解特征值的问题,可以表示为 (K-ω2M)A=0 (17) 式中:K为刚度矩阵K=Ks+Kp,Ks为弹簧能量的刚度矩阵,Kp为整体结构应变能的刚度矩阵;M为结构的质量矩阵;A为未知的系数向量;ω为圆频率。 试函数中的截断项数M、N的取值和弹簧刚度取无穷时的实际计算值对结果的精度有很大的影响,本次收敛性分析针对以上两个量进行。 选用四边自由和固支的矩形板进行收敛性分析,几何参数如下:长a=2 m,宽b=1 m,厚度h=0.02 m。板的材料参数为:杨氏模量E=2.1×1011Pa,泊松比μ=0.3,密度ρ=7 850 kg/m3。 首先对截断项数进行收敛性分析。表2给出刚度系数为0时,不同截断项数M=N=q时对应的前10阶固有频率。 表2 矩形板固有频率随截断项数的变化 从表2可知,随着截断项数M,N的增加,矩形板的自由振动固有频率趋于一致。当M=N=12时,认为算例已经收敛,以下计算中取M=N=12。 对弹簧的刚度系数进行收敛性分析。在处理固支等边界时需将边界弹簧的刚度系数取为无穷,实际计算时需要用一个较大的值来代替。表3为弹簧刚度系数取不同值时固有频率的变化。算例中假设k和K均取同一数值,即k=pN/m2,K=pN/rad,D为板的弯曲刚度值。 表3 矩形板固有频率随弹簧刚度的变化 表3中数据表明:随着刚度系数的逐渐增大,固有振动频率逐渐收敛。当刚度系数K和k的数值大小均为108D时已经收敛。故在弹簧边界刚度为无穷大时,将弹簧刚度系数值取108D代入计算即可。 本节验证方法计算直边板、斜边板、曲边板及不规则形状板自由振动的准确性,方法计算薄板问题效率较高,应用MATLAB,得到较为精确的前10阶固有频率的时间仅需约40 s(PC,4 GHz,16 GB)。 2.2.1 矩形板的弯曲自由振动分析 (18) 式中:fref为文献结果或者有限元解。 表4 矩形板固有频率 从表4可知,两种结果对比误差很小,说明本方法计算直边板的自由振动时的准确性。 2.2.2 三角形板的弯曲自由振动分析 为验证本文方法计算斜边板的准确性,对不同边界条件下三角形板的弯曲自由振动频率进行分析(物理模型见图6)。 图6 三角形板物理模型 2.2.3 椭圆形板的弯曲自由振动分析 为验证本文方法求解曲边板自由振动的准确性,下文将对在不同边界条件下的椭圆形板自由振动进行分析(物理模型见图8)。 图7 简支边界条件下三角形形薄板高阶振型与ansys软件对比图 表5 简支三角形板的无量纲固有频率 图8 椭圆形薄板物理模型 椭圆板长轴a=4 m,短轴b=2 m板厚h=0.05 m。选取简支和固支边界条件对其进行分析。 从表7可知,本方法计算结果与有限元(Ansys)结果吻合良好,最大误差不超过2%。图9给出了固支边界下前四阶模态振型图,证明了本方法的准确性。 2.2.4 曲边梯形板的自由振动分析 综合上述几种形状,为了说明本方法求解复杂形状平板自由振动特性的准确性,本节研究了带有曲边的梯形的自振特性,模型如图10所示。其中“②”号和“④”号边为曲边,其参数如下:上底长a=4 m,下底长b=10 m,高c=8 m,两斜边为1/4椭圆曲线,其中长轴为8 m,短轴长度为3 m。用本方法计算该曲边梯形板的固有频率,并与Ansys软件结果进行对比。 表8给出前10阶固有频率结果对比。从表8可知,两种方法结果吻合良好,误差不超过1%。表明本文方法在计算曲边直边组合形状时的准确性。 表6 两斜边简支底边弹性边界下三角形板固有频率 (a) (b) (c) (d) 表7 椭圆形薄板自由振动固有频率 表8 曲边梯形板固有频率 图10 曲边梯形板 本文基于改进Rayleigh-Ritz法对复杂形状薄板的自由振动问题进行分析。首先以矩形板为例进行收敛性分析,再对矩形、三角形、椭圆形和曲边梯形板的计算结果与有限元结果进行对比,证明了本方法的准确性。给出本文方法的低阶和高阶振型图与有限元的振型图进行对比,直观地看到振型吻合很好。可以得出结论:改进的Rayleigh-Ritz法在计算复杂形状板的振动问题上具有良好的收敛性、准确性和适应性。本文的方法从理论上可以拓展到对复杂形状中厚板、厚板、功能梯度板、壳类动态问题的求解。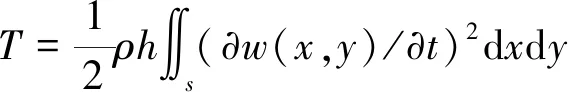

2 数值分析
2.1 收敛性分析
2.2 准确性分析
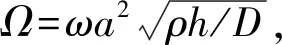
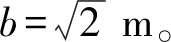




3 结 论
