轴向冲击作用下杆的弹塑性动态屈曲准则
2019-10-21张伟贵
刘 赛, 张伟贵, 肖 凯, 苏 玲, 王 悦
(1. 中国运载火箭技术研究院, 北京 100076; 2. 中国科学院空间应用工程与技术中心, 北京 100094)
梁杆结构的动态屈曲准则是进行工程设计的必要依据,现有梁杆结构的动态屈曲准则可以分为三类:一类是以分叉理论作为基础的屈曲准则[1-4],仅用于某些冲击速度较高的能列出解析方程求解的简单工况,而且一般分叉解距离失稳解较远,不满足工程需要;第二类是基于放大函数法的失稳准则[5-7],但得到的临界载荷多依赖人为主观判断;第三类是基于载荷-响应曲线的B-R(Budiansky-Roth)运动准则[8-10],此类准则适于工程应用,但需要测量的物理量种类较多。因此亟待有一种不仅满足梁杆结构工程需要,而且涉及的物理量测量简便的动态屈曲准则。
本文针对文献[11]的试验研究对象,采用文献[12]中仿真精度较高的有限元模型,进行不同重物冲击速度下扁长杆的动态响应分析,研究杆发生弹塑性动态屈曲的准则,以及初始条件参数(材料屈服应力、预制弓形幅值和截面尺寸等)对临界冲击速度的影响。
1 扁长杆冲击屈曲的仿真分析模型
在文献[11]的试验中,矩形截面扁长杆的一端铰支,另一端为加载端,如图1所示。一质量为369 g、速度为2.45 m/s的重物撞击扁长杆的加载端,重物的侧向运动受到约束,使得扁长杆加载端运动等效于滑动铰支移动。扁长杆长度、截面宽度和厚度分别为193 mm、8.7 mm和0.63 mm,扁长杆预制为微弓形,其定义见表1。材料为Ni-Cr合金钢,密度为7.8 g/cm3,弹性模量为206 GPa,屈服强度为1 470 MPa。
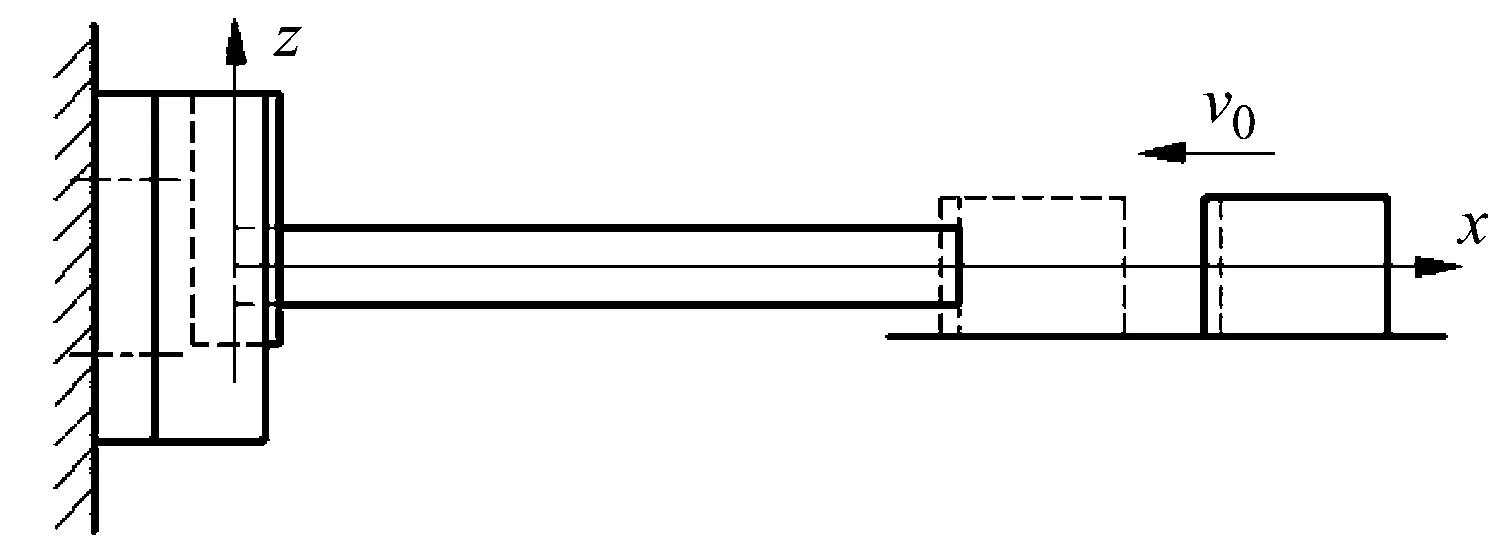
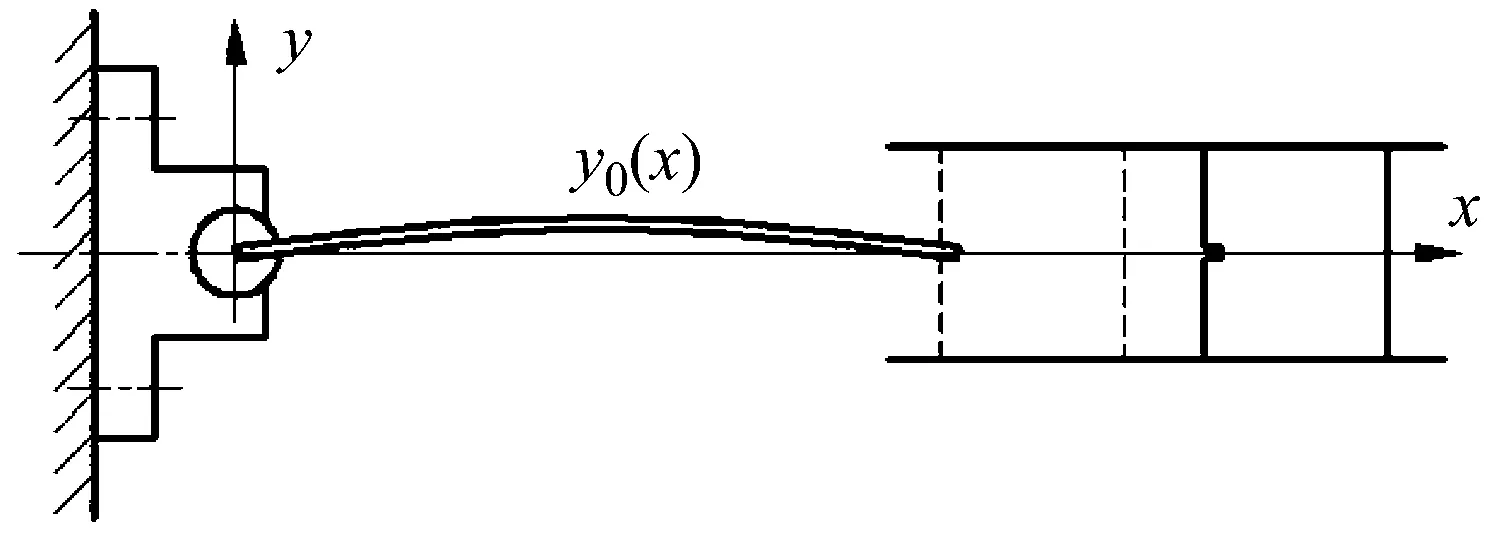
图1 受重物冲击的微弓形扁长杆[13]
显式动力学有限元仿真分析模型网格如图2~图4所示。参考文献[12]对单元类型和单元尺寸的探讨,采用单点积分8节点实体单元建模,扁长杆的实体单元尺寸为0.16 mm。有限元模型的边界条件参数取文献[12]辨识出的改进边界条件参数。扁长杆的材料模型为线性随动强化弹塑性模型,应变率效应使用Cowper-Symonds模型,参数如表2所示。其他部件均使用线弹性材料模型,参数如表3所示。仿真分析结果达到了较高的精度,如图5和图6所示。
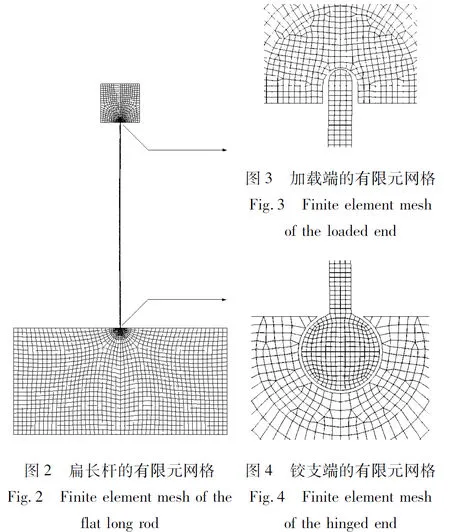

表1 扁长杆的预制微弓形

表2 扁长杆的材料模型参数
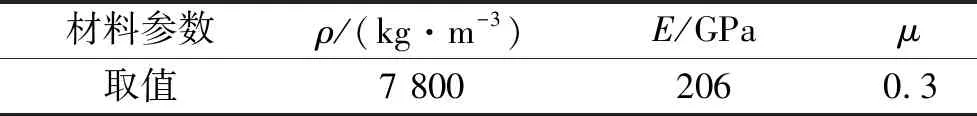
表3 其他部件的材料模型参数
2 轴向冲击作用下杆的动态响应
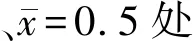
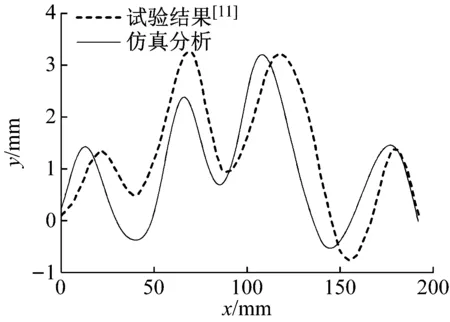
图5 t=0.75 ms扁长杆的屈曲变形曲线
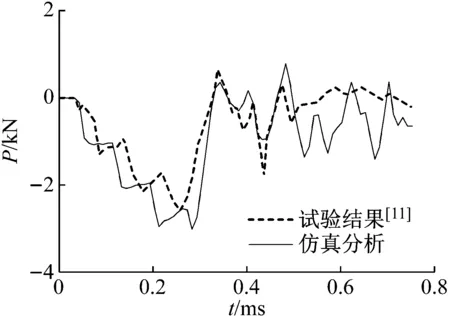
图6 扁长杆处轴向力
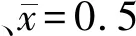
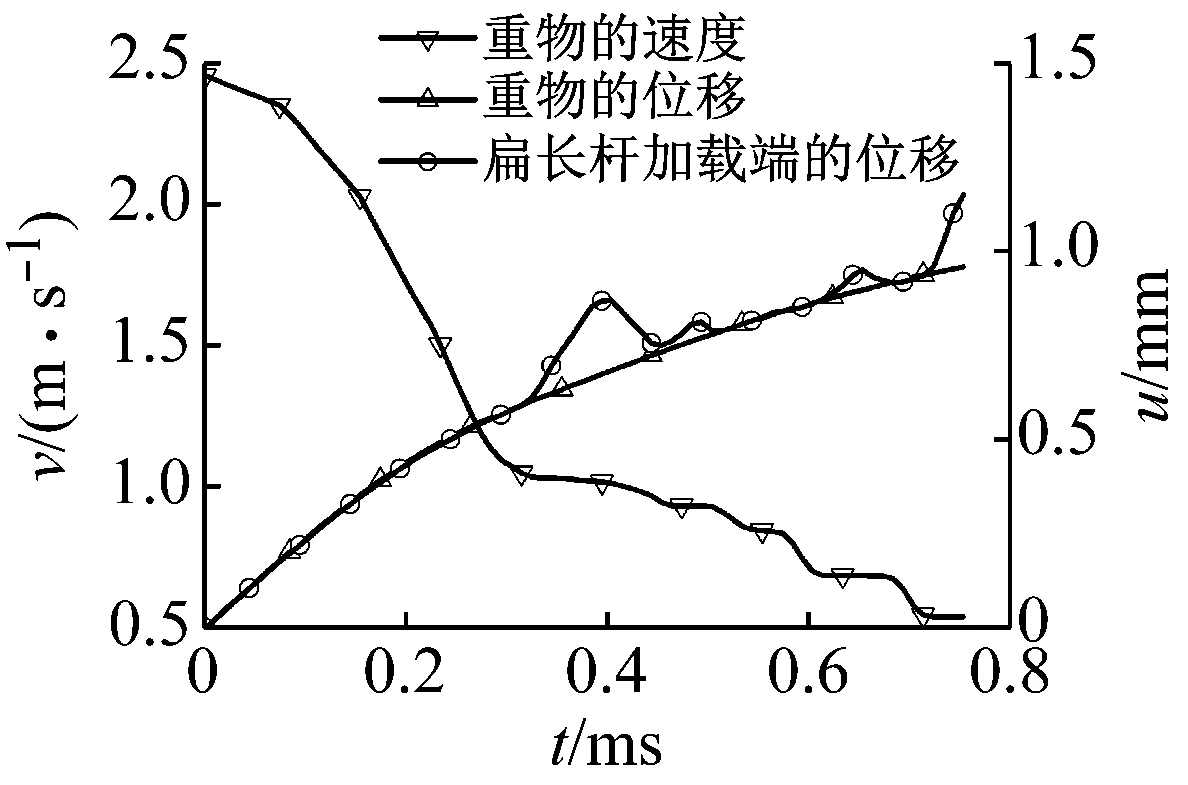
图7 重物冲击速度为2.45 m/s时重物的速度、位移和扁长杆加载端位移
Fig.7 Velocity and displacement of the weight and displacement of the loaded end under the impact velocity 2.45 m/s
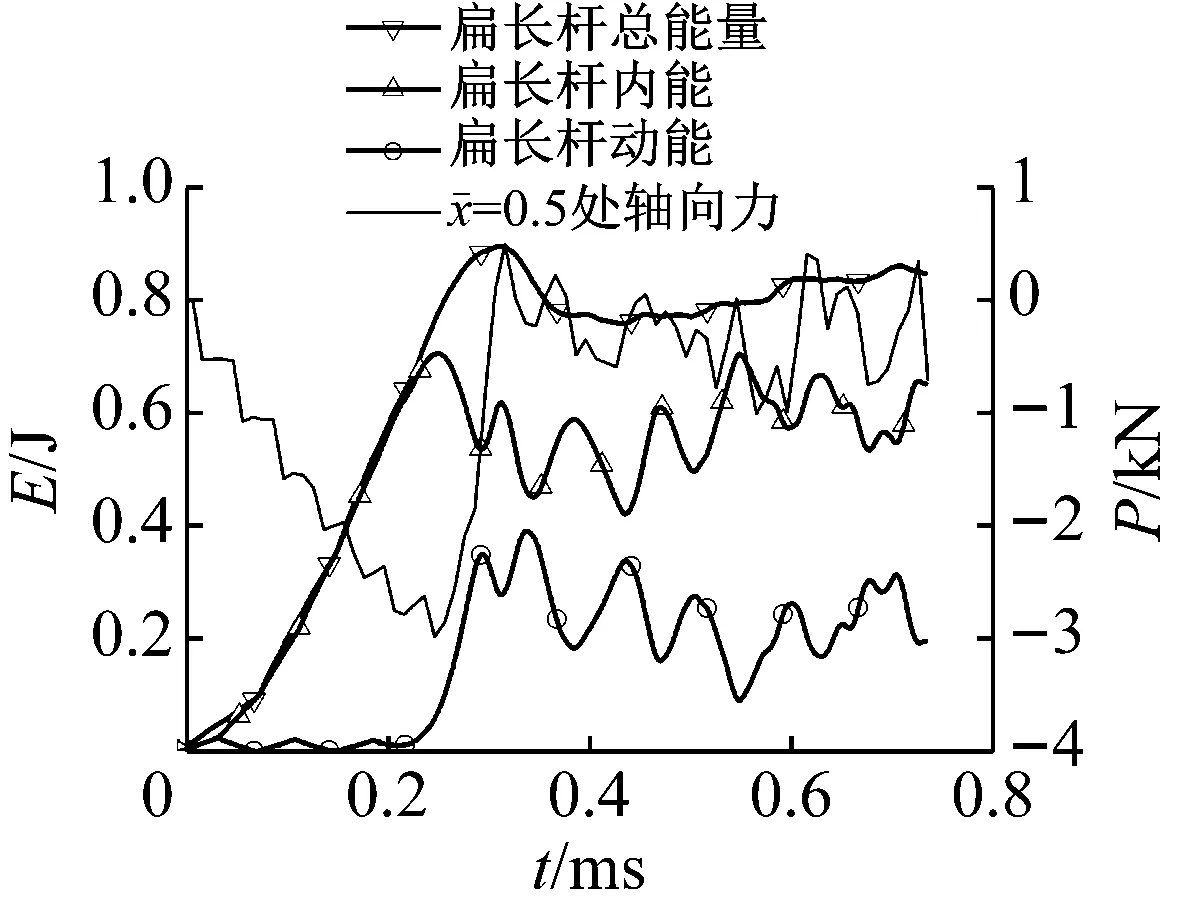
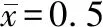
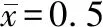
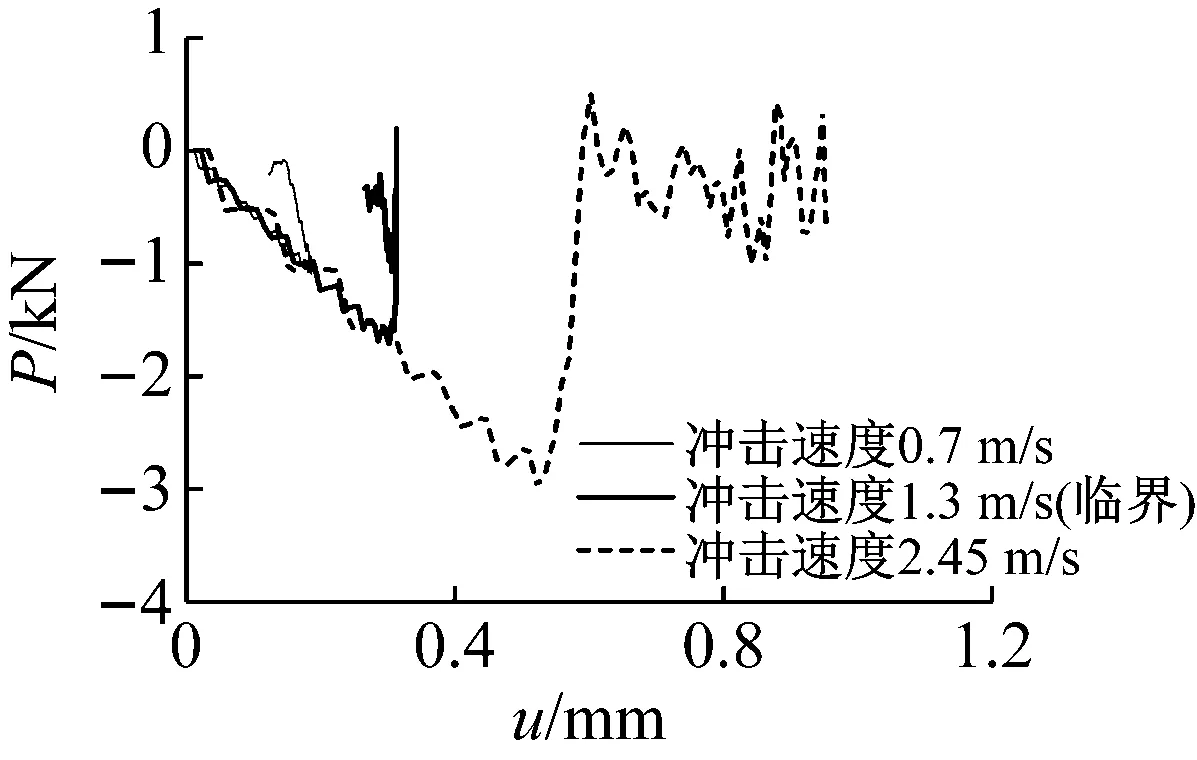
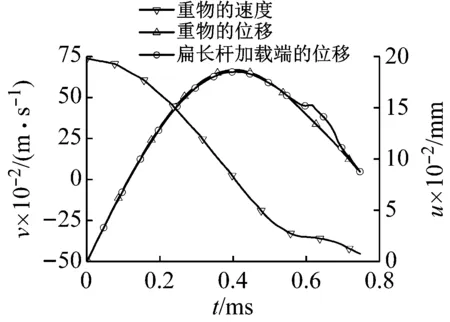
图10 重物冲击速度为0.7 m/s时重物的速度、位移和扁长杆加载端位移
Fig.10 Velocity and displacement of the weight and displacement of the loaded end under the impact velocity 0.7 m/s
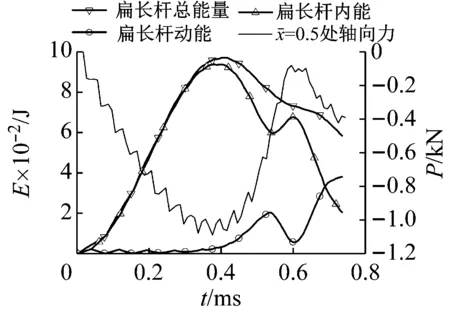
图11 重物冲击速度为0.7 m/s时扁长杆的能量和处轴向力
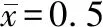
根据B-R运动准则,通过多次改变仿真分析模型的冲击速度,得到扁长杆的临界冲击速度为1.3 m/s,临界状态见图9,图12和图13,扁长杆的轴向力下降,重物短时静止,内能下降,扁长杆的加载端与重物发生明显分离——这些现象同时发生。
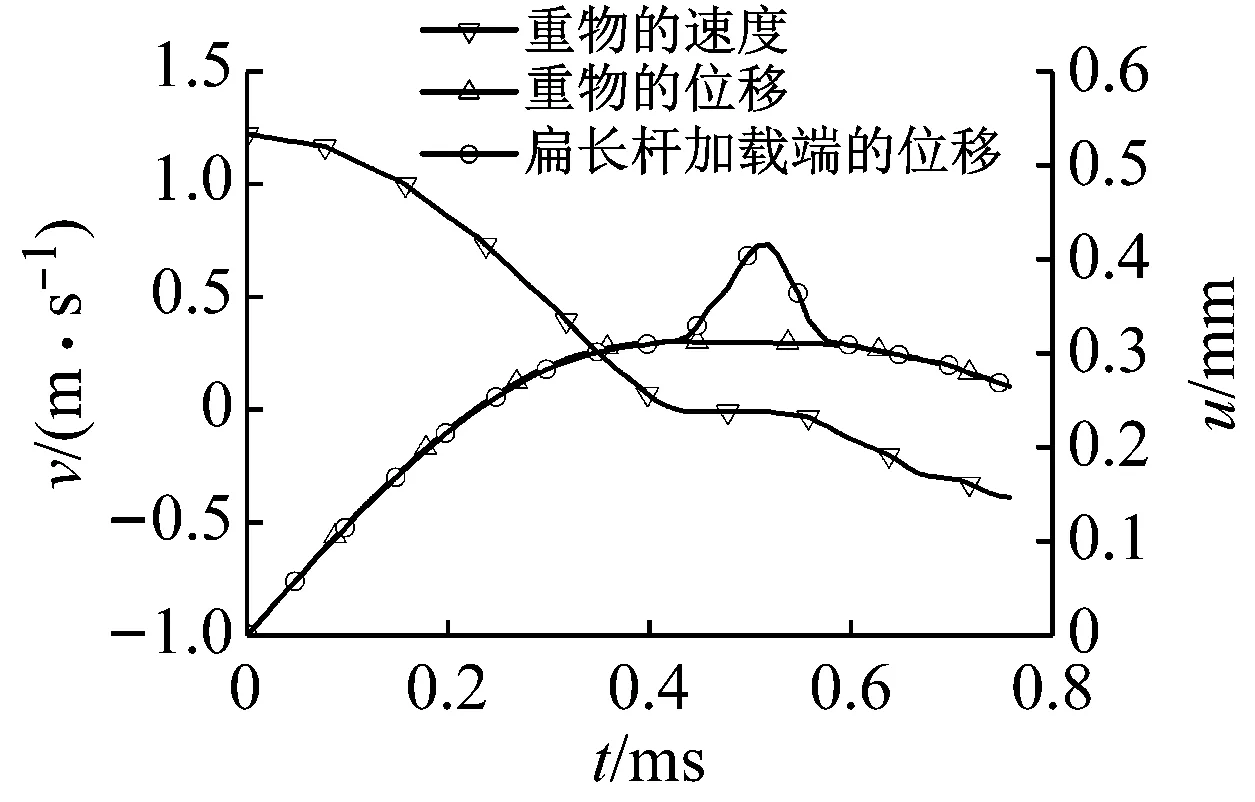
图12 重物冲击速度为1.3 m/s时重物的速度、位移和扁长杆加载端位移
Fig.12 Velocity and displacement of the weight and displacement of the loaded end under the impact velocity 1.3 m/s
3 轴向冲击作用下杆的弹塑性动态屈曲准则
随着重物冲击速度的增加,扁长杆依次出现弹性振动和弹性动态屈曲——两种不同的动态响应。比较两种动态响应的统计量特点表明,存在三种等价的判断准则:① 杆在轴向加载过程中,轴向力突然下降(B-R准则);② 杆在轴向加载过程中,内能突然下降或动能突然上升;③ 杆在轴向加载过程中,杆的加载端与重物发生明显的分离。
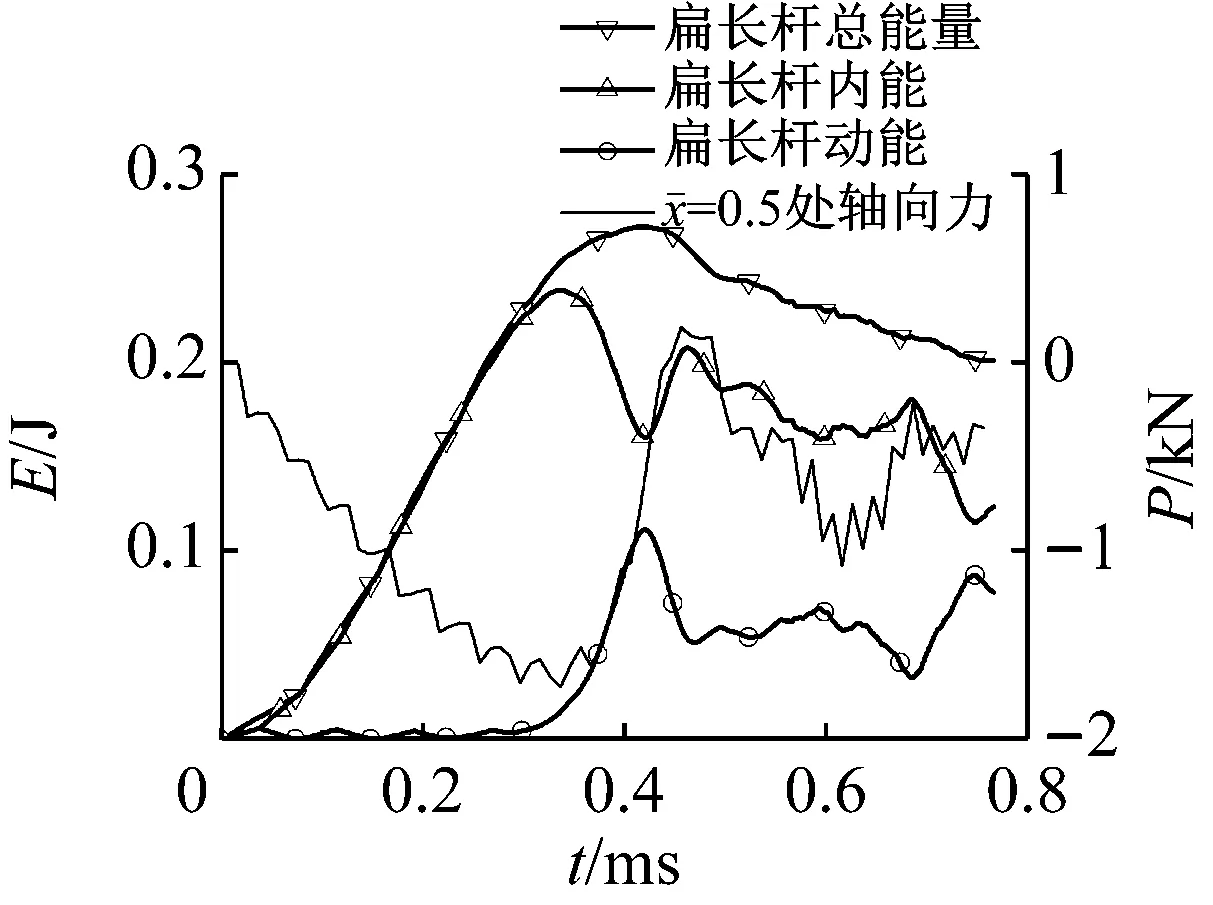
图13 重物冲击速度为1.3 m/s时扁长杆的能量和处轴向力
后两者存在一定的内在关联,扁长杆的内能突然下降时,其动能突然上升,表明扁长杆横向的屈曲速度和轴向的运动速度突然增大,导致了扁长杆的加载端与重物发生明显的分离。第③个准则较第②个更适合工程应用,可将其定义为加载分离准则,其数学表达式如下(参考坐标系见图1):
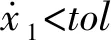
若杆的加载端与重物未发生明显分离,则发生弹性振动。虽然加载分离准则只是通过数值试验总结而来,尚未有较深刻的力学理论支撑,但数值试验表明,加载分离准则和B-R运动准则识别的扁长杆动态屈曲的临界冲击速度是一致的,均为1.3 m/s。B-R运动准则需要重物位移和轴向力两个物理量,属于两类物理量,试验中需要分别使用位移测量系统和应变测量系统测得,而加载分离准则需要加载端位移和重物位移两个物理量,属于同一类物理量,试验中仅需使用位移测量系统测得。加载分离准则减少了需要测量的物理量种类,应用更加简捷。因此从判别方法的实用性和临界冲击速度的识别精度而言,加载分离准则可以满足工程需要。加载分离准则和B-R运动准则都不能判断杆发生的是弹性动态屈曲还是塑性动态屈曲。
4 扁长杆的初始条件参数对临界冲击速度的影响
对于工程实际问题——如何提高一定长度杆件的动态屈曲强度,一般的途径都是更换比较强的材料、提高加工精度或增大截面尺寸,本文从三方面着手:① 将第1节扁长杆的初始条件参数(材料屈服应力、预制弓形幅值和截面尺寸等)作为归一化的参考值,通过大量数值计算,得到扁长杆的初始条件参数归一化值与临界冲击速度的关系曲线,如图14所示。当一个参数变化时,其余参数是不变的,仍旧为1;② 大量数值计算表明,加载分离准则和B-R运动准则识别的扁长杆动态屈曲的临界冲击速度是一致的,这也说明了加载分离准则的一般性和有效性;③ 图14表明,屈服应力仅在低于350 MPa时对临界冲击速度的影响显著,因为扁长杆此时发生塑性动态屈曲,高于此屈服应力时发生弹性动态屈曲;微小的预制弓形可明显降低扁长杆的动态屈曲强度;增大截面尺寸是提高扁长杆动态屈曲强度的较有效途径。
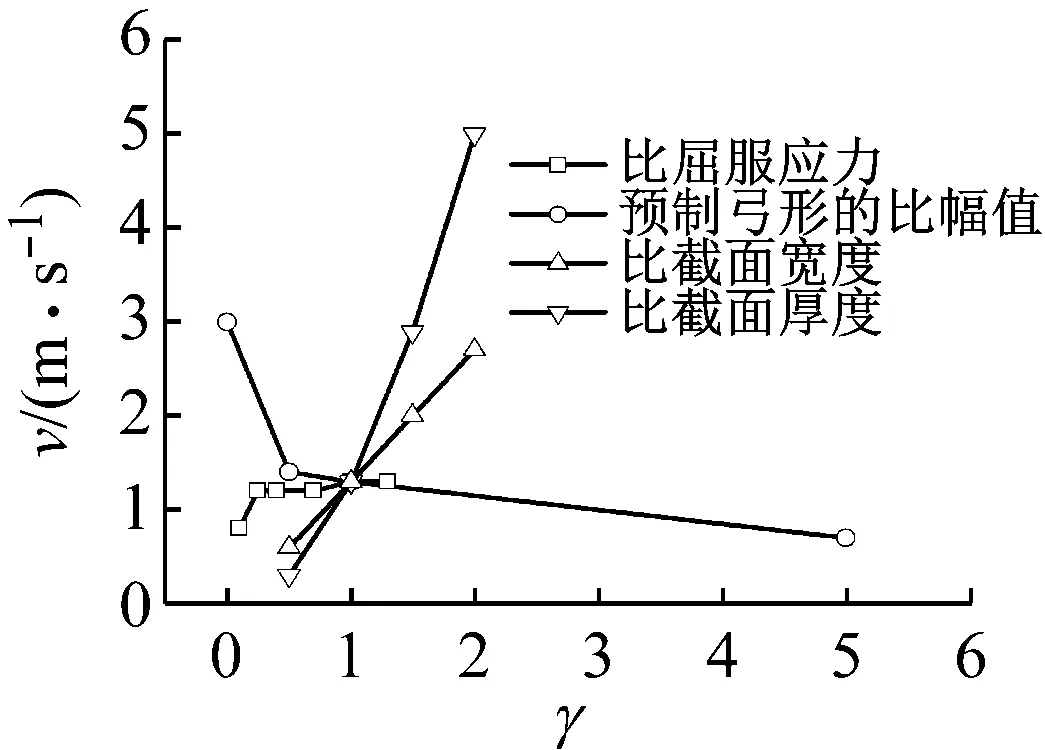
图14 扁长杆的初始条件参数归一化值与临界冲击速度关系
5 结 论
(1) 通过不同重物冲击速度下扁长杆动态响应的有限元分析,提出了杆在轴向冲击下的动态屈曲准则——加载分离准则:重物对杆的轴向加载过程中,杆的加载端与重物发生明显的分离。
(2) 虽然目前没有较深刻的力学理论支撑,但与B-R运动准则相比,加载分离准则同样可以满足工程需要,但涉及的物理量测量更为简便。
(3) 进一步分析了扁长杆的初始条件参数(材料屈服应力、预制弓形幅值和截面尺寸等)对临界冲击速度的影响规律,验证了此准则的一般性和有效性,总结了提高此种杆件动态屈曲强度的有效措施:与提高扁长杆的材料强度和加工精度相比,增大截面尺寸是提高其动态屈曲强度的较有效方法。
本文的研究成果具有一般性意义,适用于其它梁杆结构的动态屈曲问题,也有助于其它结构的动态屈曲准则的发展。
