非线性弓形弹簧的设计与仿真

侍红岩

(内蒙古民族大学)

1.引言

弓形弹簧是一种特殊形式的弹簧，最初主要应用于箭术【1】方面，工业上应用的相对较少。它属于一种介于板弹簧和片弹簧之间的弹簧，其潜在应用领域很广。目前主要的应用还是在油井开采过程中，弓形弹簧套管扶正器【2】作为一种辅助工具使用，也可以作为压缩弹簧【3】或是减震弹簧【4】使用。但就目前来看弓形弹簧的建模方法比较少见，已有的设计方法与弓形弹簧的实际性质差距较大。对于弓形弹簧来说对机械特性（弯曲形状和变形力）进行建模比较难，因为其内力、力矩和几何形状都是未知数，而且其间的关系不是很明确。而且该系统的唯一闭合解对研究人员来说用处不大。

对弓形弹簧进行机械分析比较难，因为其几何形状与内力和力矩错综复杂地结合在一起，而内力与力矩的力学分析比较直观，最难不过为二阶单变量积分。但是，弓形弹簧的几何形状不能简化为单微分方程。现有文献中很少有关于弓形弹簧几何变形与力之间关系的描述。

采用标准力学分析技术进行兼容性分析。设弓形弹簧的长度为L，弓形弹簧首尾之间的变形为D，将弓形弹簧弯曲进行安装。因为弓形弹簧弯曲后的形状既不是抛物线也不是圆弧。因此外力与变形之间是非线性的关系，对这种非线性关系的求解只能采用近似求解的方法。需要事先给定一些假设条件，首先我们假设弓形弹簧各段的材料性质一致，其次假设受力过程中所施加的外力大小和方向已知，另外假设弯曲过程中弓形弹簧的中点位置没有发生移动，最后假设变形过程在安全系数范围内进行。

2.弓形弹簧的设计与建模

弓形弹簧在工业上的应用主要是作为支撑和控制变形位移量的工件。根据其在实际应用中的受力情况，发现通常弓形弹簧的受力点有两种。一种是外力作用在弓形弹簧的两端，另一种是外力作用在弓形弹簧的对称中点。不管是哪个位置作为受力点，弓形弹簧受力后都会出现长度（端到端的直线距离）和宽度（中点的切线到两端连线的垂线）方向的变化。通过控制这两方向变化的大小就可以控制相应所需的位移量，可以是某一个方向上的，也可以是两个方向综合作用下的。

图1 弓形弹簧受力变形过程

本文研究的受力点为在弓形弹簧两端受大小相等的力。弓形弹簧为纯弯曲薄片状，厚长比大于100。本文采用弯曲梁受力的分析过程来近似分析弓形弹簧的受力过程，为了便于分析，作出以下假设：材料为均匀的各向同性材料；变形过程中中点的位置不发生相对移动；对称部分的变形是同步的；弓形弹簧在手里变形时，其内部应变-应力关系是线弹性的，并且弹性变形相对较小。

弓的内力矩与二力轴的位移成正例【5】。显而易见从弓的任何部分截取一段，在其上都有内力矩M与Fy相等，F是端对端弹簧力，y是到载荷轴到中点的垂直距离。 为弓形弹簧一侧的曲线段的切线（切点为弓形弹簧的末端）与水平线的夹角，定义为弯曲角。这个角度随着弓形弹簧的受力会发生相应的变化。因为弹力不随切入的位置改变，发现。另外，根据曲率公式可知：

截取弓形弹簧上一个微小的片段，得：

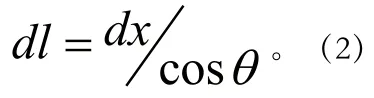
而曲率也可写成：

将公式（2）代入上式，得：

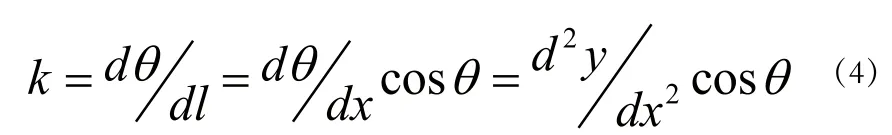
将公式（4）代入公式（1），得

对公式（5）进行两次积分，得：

即：

假设弓形弹簧的中心对称点在受力过程中没有相对位移，则根据边界条件：，得到，。那么公式（6）就可写成：

上面这个公式表达了在假设条件下的弓形弹簧所受载荷与变形之间的关系。从中可以得到载荷与宽度变形、长度变形以及长宽综合变形之间的关系。从这个公式中还可以看到，弓形弹簧的形状会随着载荷的变化而出现非线性的变化。

3.弓形弹簧的仿真模拟

由于弓形弹簧力与变形之间存在这非线性的关系，而且在公式中存在着四个未知量，所以用一般的数值算法很难进行精确求解。为了得到弓形弹簧变形与受力之间的关系，本文采用MATLAB编程语言对弓形弹簧进行建模【6】，运用迭代的方式计算弓形弹簧弯曲部分的力学特性。改变其中的某些参数就可以看出得到不同性能的弓形弹簧的机械性能，从而用来分析各个变量对于弓形弹簧的机械性能影响程度。对于弓形弹簧来说，初始状态对其力学性能的影响大小可以通过下面的曲线知道，

下面是四条力与变形的曲线，初始参数EI=78，L=1m，dmax=0.29m，四条曲线的初始弯曲角分别为KAngle=0.05，0.1，0.15，0.2弧度。从曲线图中可以看出，每条曲线的在变形小于0.02m的情况下，其斜率会有很大的不同，但是在变形大于0.05m时逐渐趋于同样的斜率值收敛。从中可以看出初始弯曲角对弓形弹簧的影响还是比较大的，当初始弯曲角比较小的时候，弓形弹簧在外力作用下比较容易变形，而初始弯曲角比较大的时候，会比较难变形。但是，当变形量达到一定值的时候，初始弯曲角的大小对变形的影响就可以忽略不计了。而在变形量为0.02m至0.05m之间时，不同初始变形角的弓形弹簧均出现了曲线斜率的突变。初始变形角越小，这种突变出现的越早，也就是说所需的外力越大。在经过这个突变后，变形量的大小与外力

之间逐渐趋于正比关系。

图2 形变量与外力之间的模拟关系

4.试验结果对比分析

用弹簧钢加工出一组长度为1m，宽度为0.03m，厚度为0.005m，初始弯曲角为0.05弧度的弓形弹簧，在力学测试仪器上进行力学性能对比测试。中点位置固定后，对两端进行加载，所加载荷为仿真实验所测得数据，可以得到相应的实测变形量。将仿真变形量与实测变形量进行对比，如表1。

图3 形变量与外力之间的实验关系

上图中曲线代表仿真数据，点线代表实测数据，从中可以看到实测曲线与仿真曲线大致相同，两者的差异相对来说不是很大，最大的差异出现在变形量为0.03m，处，仿真值为193.1N,而实验值为217.5N，相对误差达到了11%。这个最大误差出现在弓形弹簧弹性的过渡期，也就是说弹簧对变形的抵抗强度从强变弱的过渡期。经过了这段线段后，误差在逐渐减小，最小的误差接近于0。

这个误差变化产生的原因有几个，其一是实验件加工中存在的误差。其二是实验中测位移和力的准确度不高。最主要的是因为在仿真建模中引进了假设的部分，并且对宽度没有具体的限定。

5.结论

弓形弹簧并不是新型弹簧，只是对它的研究和应用比较少，但这并不表明弓形弹簧没有应用价值。对一些跨度大，空间有限，变形量大的实际应用方面还是有很大的使用前景。从上述模拟和实验的结果来看，可以采用避开弓形弹簧非线性变形的部分，利用它近视线性变形的部分进行实际应用，就可以合理有效地发挥其最大作用。目前急需对它进行更全面和深入地研究。

【参考文献】

1. Ihor Zanevsky。Compound archery bow asymmetry in the vertical plane[J]。Sports Eng ,2012 15:167-175

2.陈智等。一种弓形弹簧的设计与应用[J]。石油机械，2010，38(8)，:71-73。

3. Dale A. Lawrenc。Bow Spring/Tendon Actuation for Low Cost Haptic Interfaces。First Joint Eurohaptics Conference and Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems , 2005:157-166。

4.凌荣江。汽车板簧的建模及非线性分析[D]。南京航天航空大学，硕士学位论文，2008。

5 付茂林。一类新的非线性动力系统的稳定性分析[J]。南华大学学报，2002，16（4）:15-17.6. 马金奎.。基于MATLAB的弹簧优化设计新方法[J]。机床与液压，2004，12:99-101。