不均衡闸瓦压力作用下转向架前后轮对非对称运动

2019-10-19刘鹏飞王开云张凯龙曹云强

中国铁道科学 2019年5期

刘鹏飞，王开云，张凯龙，曹云强

(1.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，河北石家庄 050043；2.西南交通大学牵引动力国家重点实验室，四川成都 610031)

闸瓦制动在铁路机车车辆上已得到长期的广泛应用，其性能好坏对列车运行安全性至关重要。长期以来，关于闸瓦制动的研究主要从制动力作用下的动力学问题和闸瓦自身摩擦引起的热—机耦合等2个方面开展。严隽耄等[1]较早的系统论述了闸瓦制动力作用下的列车纵向冲动行为，并对轮轨接触特性进行了研究；陈光雄等[2]专门研究了闸瓦制动引起的颤振及噪声问题；COLE等[3]对列车制动时的不稳定行为也进行了讨论；ZHANG等[4]研究了制动力矩对货车动力学性能的影响，指出制动力矩的作用会改变车辆某个方面的动态特性；李亨利等[5]分析了闸瓦制动力对轮轨接触力学的影响，指出闸瓦力及制动力会改变轮轨接触和蠕滑关系；LIU等[6-8]综合车辆—轨道耦合动力学和列车纵向动力学研究方法，分析了动态车钩力与闸瓦制动力联合作用下轮轨耦合振动特性；杨广雪等[9]指出闸瓦制动产生的压应力通过与热处理的残余应力叠加可抑制车轮腹板疲劳损伤。应丁之[10]、孙可心[11]、张金煜等[12]从闸瓦制动性能试验、闸瓦偏磨、轮瓦热交换及制动温度场等角度对闸瓦自身的力学及传热特性进行了研究。

运营实践表明，尽管机车车辆会在一定周期内对闸瓦制动机构进行检修，仍会因结构损坏、部件变形、闸瓦磨耗等问题，无法避免闸瓦压力不均衡问题的出现。如早在2008年，17025次列车就因闸瓦磨耗不均导致制动力不均衡，制动力大的闸瓦与车轮相磨产生冒火星现象而被拦停[13]；2016年，大秦铁路公司C80型货车112块闸瓦的压力测试结果显示，列车管减压50 kPa时，闸瓦压力从0～4.69 kN不等分布，引起了车辆抱闸故障[14]。同一轮对左右侧不均衡的闸瓦压力除影响制动力有效发挥外，无疑还会对轮对形成附加的摇头力矩(简称闸瓦力矩)。众所周知，轮对的摇头和横移运动姿态很大程度上反映了轮对自身的蠕滑导向能力，那么在闸瓦力矩作用下，轮对的运动行为会发生何种变化是值得深入探究的科学问题，且是机车车辆存在的共性问题，尚未引起关注。同时，摸清这一规律，对于指导转向架基础制动系统的改进设计和检修具有重要意义。

本文从简单的六自由度转向架模型出发，忽略非线性因素，研究闸瓦力矩作用下二轴转向架前、后轮对的横移和摇头动态响应，以突出单纯闸瓦力矩的作用效果，揭示前、后轮对非对称运动的本质。进而，考虑轮轨蠕滑非线性，以整车动力学模型为例，进一步检验简化模型反映的基本规律，最后讨论关键因素对轮对运行姿态的影响。

1 闸瓦力矩作用下转向架受力状态

以弹性约束单轮对为例，考虑其静平衡条件下的受力状态和动作过程，研究闸瓦力矩改变轮对运动状态的基本原理。

闸瓦力矩作用下单轮对运动如图1所示。当轮对承受顺时针闸瓦力矩M时，轮对势必相应产生1个正向摇头角φw，由轮轨蠕滑理论可知，轮轨横向蠕滑力与摇头角满足式(1)，因此作用于轮对上的合成横向蠕滑力Fy为正向，推动轮对正向移动，产生横向位移yw，之后由于踏面具有锥度，右轮滚动半径增大，左轮滚动半径减小，左、右轮对间形成式(2)给出的纵向蠕滑力，且其合成的纵向蠕滑力矩与闸瓦力矩M方向相反，纵向蠕滑力矩的逐渐增大直至与力矩M相互抵消，轮对才达到新的平衡状态。当轮对为弹性约束状态时，纵向蠕滑力矩与弹性约束力矩将同时作为反力矩以抵消力矩M，这一状态下面通过转向架模型进行细致讨论。

Fy=2f22φw

(1)

(2)

式中：FLx和FRx分别为左、右车轮纵向蠕滑力；r0为车轮名义滚动圆半径；f11和f22分别为纵向和横向蠕滑系数；λ为车轮踏面锥度。

图1 闸瓦力矩作用下单轮对运动

为突出转向架基本受力状态和轮对蠕滑导向过程，这里研究对象仅限于1个普通的二轴转向架。图2给出了轮对弹性定位的二轴转向架直线运行力学模型，其中轮对和构架只考虑横移和摇头自由度，整个转向架共计6个自由度。一系和二系悬挂也只考虑各自的纵向、横向悬挂刚度；由于只进行静平衡分析，忽略悬挂系统中的阻尼作用和速度项。图中，FpLi和FpRi分别为i位轮对左、右侧闸瓦压力；Mi为将i位轮对两侧的闸瓦压力等效后的闸瓦力矩；其余相关符号的含义和取值见表1，为典型铁路客车基本参数，可参见文献[14]中附录6。

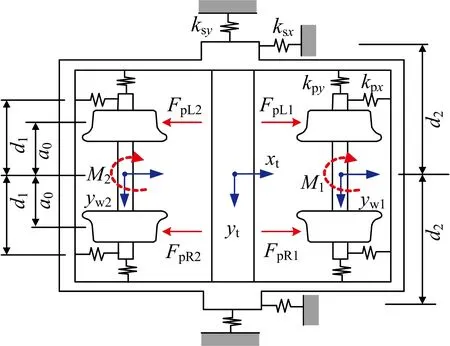
图2 二轴转向架直线运行力学模型

表1 转向架动力学建模参数

忽略蠕滑力和各悬挂元件的非线性特性，推导出转向架各部分的平衡方程为

2kpy(yw1+yw2-2yt)-2ksyyt=0

(3)

kpφ(φw1+φw2-2φt)+2ltkpy(yw1-yw2-

2ltφt)-ksφφt=0

(4)

2kpy(yt-yw1+ltφt)+2f22φw1=0

(5)

(6)

2kpy(yt-yw2-ltφt)+2f22φw2=0

(7)

(8)

其中，

式中：kpφ，ksφ分别为一系、二系悬挂摇头角刚度；yt和φt分别为构架的横向位移和摇头角；yw1和yw2分别为前、后轮对的横向位移；φw1和φw2分别为前、后轮对的摇头角。

式(3)—式(8)依次为构架横移、构架摇头、前轮对横移、前轮对摇头、后轮对横移和后轮对摇头的平衡方程，构成典型的一组线性方程组。对6个自由度转向架模型，采用高斯消元法对式(3)—式(8)求解，即可得到各部件的运动状态。

2 闸瓦力矩作用下前后轮对非对称运动

设置2个计算工况：(1)工况1，闸瓦力矩仅作用于1位轮对即前轮对(M1≠0。M2=0)；(2)工况2，同等大小的闸瓦力矩仅作用于2位轮对即后轮对(M1=0，M2≠0)。这样，通过在前轮对、后轮对分别施加闸瓦力矩，便于分析制动时闸瓦力矩对各轮对运动状态的影响方式和影响程度。

综合考虑构架和轮对运动，得出轮对和各部件横移量和摇头角随正向(顺时针方向)闸瓦压力的变化规律如图3所示。图中，实线、虚线分别代表工况1和2的计算结果，以下同理。由图3可以看出：工况1中，前轮对、构架、后轮对均发生了较大的横移，闸瓦力矩为15 kN·m时前、后轮对最大横移量分别达到7和5.3 mm，而工况2中，各部件的横移量均保持在较低水平，后轮对最大横移量约为1.65 mm，前轮对横移量仅为0.023 mm，工况1中前轮对横移量为工况2的4倍之多；从摇头角响应来看，工况1中，前轮对、构架的正向摇头角基本相当(0.4 mrad)，后轮对则呈反向摇头，且幅值(-0.15 mrad)约为前轮对摇头角的一半，工况2中前轮对和构架呈负向摇头(-0.27 mrad)，后轮对为正向摇头(0.31 mrad)，且前、后轮对摇头角幅度大小很接近，只是方向相反。

图3 正向闸瓦力矩作用下轮对横移和摇头运动

根据图3的计算结果，给出了工况1和工况2中各部件最终达到平衡状态时运行姿态如图4所示。由图4可以看出：闸瓦力矩作用对前、后轮对的影响规律不一致，作用前轮对时更易使轮对发生轮缘贴靠现象；此外，若考虑轮对的曲线通过时，不均衡闸瓦力产生的力矩还可能引起较大的轮对冲角。

图4 闸瓦力矩作用下转向架各部件运动姿态

下面根据轮对受力平衡关系，对上述现象的产生机理作进一步论述。根据式(6)和式(8)，轮对横向位移与构架摇头角、轮对摇头角的关系可表述为

(9)

其中，

Mφi=kpφ(φt-φwi)

式中：Mφi为i位轮对受到的悬挂摇头力矩。

对前轮对施加正向闸瓦力矩，轮对会发生相应的正向摇头运动，进而产生横向蠕滑力，在横向蠕滑力作用下轮对向正向横移，此时轮对的横移和摇头均会引起构架的顺时针摇头，构架和轮对的摇头角同向，两者差值φt-φwi较小，悬挂摇头力矩Mφi相应减小，对轮对横移的影响减弱。因此，由式(9)知，较大的闸瓦力矩Mi将引起较大的轮对横移，换言之，轮对只有通过较大的横移量才能产生足够的纵向蠕滑力矩来平衡闸瓦力矩M1。对后轮对施加正向闸瓦力矩，后轮对发生正向摇头并向正向移动，轮对横移引起构架的负向摇头，同样由式(9)可看出，构架和轮对摇头位移差φt-φwi将呈负向增大，即形成的悬挂摇头力矩Mφi为逆时针增大，能有效平衡闸瓦力矩M2，因此M2与Mφi总合成力矩的量值减小，进而产生较小的轮对横移。这也就解释了为何在前轮对、后轮对上施加同样大小的闸瓦力矩，但前轮对会引起更大的横移，而后轮对的横移量较小。

至于轮对和构架摇头角变化，前轮对上作用有正向闸瓦力矩时构架呈正向摇头，释放了轮对的正向摇头运动，因此轮对有较大的正向摇头角，后轮对有闸瓦力矩时构架负向摇头，而轮对呈正向摇头，两者运动趋势互有抵抗，因此限制了后轮对的正向摇头角幅度。

当前轮对、后轮对先后作用负向(逆时针)闸瓦力矩时，在外部闸瓦力矩作用下，前轮对与构架的摇头方向始终保持一致，而后轮对的摇头方向却与构架始终相反。因此，同以上分析过程，前轮对的横移量同样大于后轮对，如图5所示。

图5 负向闸瓦力矩作用下转向架横移运动

综合上述分析结果，前、后轮对分别施加大小、方向相同的闸瓦力矩，前轮对的横移量远大于后轮对。从受力平衡角度看，造成这一非对称运动的根本原因在于，受闸瓦力矩作用的主动轮对是否能和构架保持同向摇头。当构架和主动轮对的摇头一致时，悬挂摇头力矩难以抵消闸瓦力矩，只能通过轮对较大的横移量产生纵向蠕滑力矩来平衡。当主动轮对和构架摇头运动反向时，悬挂摇头力矩抵消较大部分的闸瓦力矩，轮对较小的横移量即能产生足够的纵向蠕滑力矩使系统平衡。无论闸瓦力矩作用哪个轮对，构架摇头位移始终和1位轮对保持相近，这也充分体现了前轮对的导向作用。

3 闸瓦力矩作用下整车动力学行为

为了检验上文简化模型中的基本规律，基于车辆—轨道耦合动力学理论和表1所给参数，建立了考虑轮轨接触、减振器卸荷特性等非线性环节的客车—轨道耦合动力学分析模型，相关部件的建模方法和运动方程可参考文献[7，15]，这里不再给出。其中，轮对子模型在原基础上进一步考虑了闸瓦力矩Mi作用，轮轨切向力采用经典的Kalker简化理论求解。钢轨为CHN60轨，车轮型面采用锥形踏面(锥度为0.075)和具有非线性锥度的LM型踏面，如图6所示。

图6 锥形踏面与LM型踏面

首先对锥形踏面和LM型踏面进行比较分析，以对简化模型的反映规律进行检验。轮对上的闸瓦力矩在1～10 s内逐步增至15 kN·m目标值，总积分时间为20 s。以工况1为例，闸瓦力矩施加的过渡阶段及系统达到新平衡位置后，前转向架各部件的横移量和摇头角变化如图7所示。由图7可以看出：采用锥形踏面时，前、后轮对的横移量分别为7.51和6.20 mm、摇头角分别为0.44和-0.14 mrad，而对应图3中15 km·m闸瓦力矩作用下简化模型前、后轮对位移分别为7.0和5.3 mm，轮对摇头角分别为0.40和-0.15 mrad，可见，无论是部件横移量还是摇头角，平衡状态下其分布规律与简化模型的结果十分接近。尽管6个自由度转向架模型简化了车体参振以及其他很多非线性环节，但同样能够较好反映出闸瓦力矩作用下轮对的运动状态。而采用LM型踏面后，进一步考虑了接触几何非线性，各部件的位移趋势不变，只是幅值有所减小。可以说，闸瓦力矩对前、后轮对影响规律的不对称性，也是转向架一种特有属性。

图7 工况1锥形踏面、LM型踏面转向架动态位移比较

进一步，讨论车辆采用实际的LM型踏面，工况1(M1≠0，M2=0)、工况2(M1=0，M2≠0)转变时闸瓦力矩对轮轨作用力和轮对磨耗情况的影响。不同工况时前转向架1，2位轮对的轮轴横向力及轮对磨耗功率对比如图8所示。从图8可以看出：闸瓦力矩作用于1，2位轮对分别会产生最大4.7和4.1 kN的轮轴横向力；由于工况1中1位轮对横移量大，产生了较大的轮轨纵向蠕滑力和蠕滑率，因此最终合成的磨耗功率明显增大，轮对磨耗功率接近0.4 kW，远大于工况2中轮对最大磨耗功率0.06 kW，约为后者的6倍。

因此，从考虑轮轨接触几何非线性和力学非线性的整车动力学仿真结果看，闸瓦力矩同样造成了轮对的非对称运动，且可以推断，若闸瓦力矩作用于前轮对，将产生更为剧烈的轮轨横向动力和轮轨磨耗。

4 关键参数对转向架运动行为影响规律

考虑工况1、工况2的载荷条件，以下研究一系悬挂刚度和踏面锥度等关键参数对转向架各部件运动行为的影响规律。

图8 LM型踏面轮对轮轴横向力及磨耗功率

一系悬挂纵向刚度对转向架各部件横移量和摇头角的影响如图9所示。

图9 一系悬挂纵向刚度对转向架各部件横移量和摇头角的影响

从图9可以看出：无论是工况1还是工况2，随着一系悬挂纵向刚度增大时，构架和轮对的横移量以及摇头角均先迅速变化，然后趋于稳定。例如，一系悬挂纵向刚度从10 MN·m-1增至50 MN·m-1时，工况1中构架横移量由6.05 mm降至4.15 mm，降幅为1.9 mm，对应工况2中的构架横移量由0.81 mm增至2.9 mm，增幅为2.1 mm；一系悬挂纵向刚度在50～150 MN·m-1范围变化时，工况1和工况2对应的构架横移量分别减小和扩大了0.8和0.43 mm，由此也可看出，一系悬挂纵向刚度的增加将弱化闸瓦力矩在不同轮对上作用的效果，亦即使工况1和工况2中转向架部件位移均趋于一致。

一系悬挂横向刚度变化对转向架各部件横移和摇头运动的影响如图10所示。从图10可以看出：无论是工况1还是工况2中，增大一系悬挂横向刚度，前轮对横移变化不大，但均会使构架和后轮对有向前轮对横向靠拢的趋势，同时使各部件摇头角呈逐渐增大趋势，当一系悬挂横向刚度增至5 MN·m-1后，对摇头角的影响效果减弱。

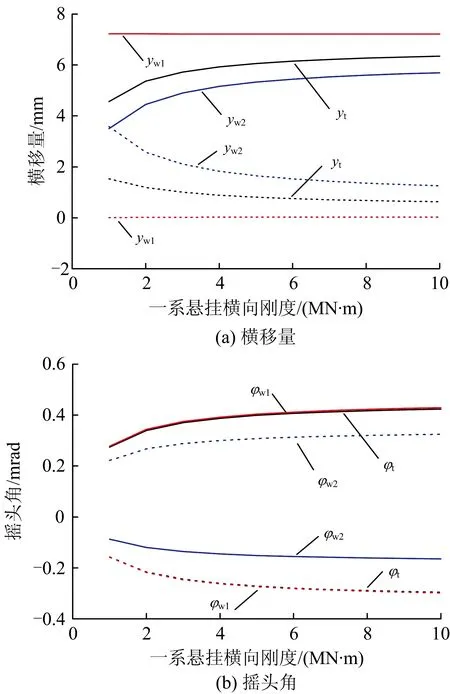
图10 一系悬挂横向刚度对转向架各部件横移量和摇头角的影响

因此，一系悬挂纵向刚度、横向刚度对转向架部件位移的影响规律截然不同。

进一步，踏面锥度变化对转向架位移的影响如图11所示。从图11可以看出：工况1中，随着踏面锥度的增大，转向架各部件横移量几乎是等幅减小的，逐渐接近对中位置，部件的摇头角也向对中位置靠拢；而工况2中，踏面锥度变化对部件横移运动影响微弱；总的来看，增加踏面锥度同样将弱化闸瓦力矩作用效果，使工况1和工况2中转向架部件位移均趋于对中位置。