引导学生思维自由生长

■华云锋

教学案例

对于图形中的计算问题，很多学生感到比较棘手，因为这类问题都离不开几何结论的证明。可以说，几何图形中的计算问题是基于“证明”之上的数量关系研究，对学生的数学综合素养要求较高。要想帮助学生渡过难关，教师就要引导学生学会发现问题、提出问题，并尝试解决问题，努力打造让学生思维自由生长的成长课堂。

添加辅助线可以对图形进行模型再构建，形成与已知信息相关联的全新图形，从而找到新的突破口，这就是所谓的“一线生机”。在教学中，教师要一步步启发学生沿着解题脉络不断思考、探索，这样，学生的数学思维才会渐进渐深，数学能力才会渐生渐长。下面，笔者试以两道图形中的计算问题的课堂教学为例，展示一下成长课堂的做法。

【问题1】如图1，半径为1的⊙O沿着△ABC的内部边缘滚动一周，回到起点D后，停止运动。已知AB=15，AC=13，BC=14，求圆心O的运动路径长。

图1

图2

图3

师：解决路径长的问题，我们首先需要做什么呢？

生：画出动点的运动路径。

师：如图2，我们发现圆心的运动路径长就是△O1O2O3的周长。那么如何求这个三角形的周长呢？

生：我想到2017年盐城市中考卷中一道类似的题目，那道题是以特殊角为切入口，运用三角函数分别算出相关线段的长。

师：联想是解决问题的重要方法之一，值得称赞！可是本题没有特殊角，怎么办呢？

生：根据圆与三角形三条边相切的条件，可以添加过切点的半径。已知三角形的三条边长，只需再想方法求出6条切线BG、BL、CK、CM、AP、AN的长度或长度和即可。

师：你的思路完全正确。那么如何求切线的长度或长度和呢？

生：可以考虑整体求值，如图3，画A1C1∥AC且与圆O相切，这样6条切线长度之和就等于△A1BC1的周长，可是我不知道如何求△A1BC1的周长。

师：出现思维“断档”现象，可能是思考方向有问题，谁有其他思路吗？

生：我发现△A1BC1的内切圆半径为1，我想求出△ABC的内切圆半径再试试。根据图4，运用勾股定理先求出AH的长度为12，再运用面积法求出△ABC的内切圆半径IE=4。由图3的△A1BC1∽△ABC，容易证得图3的△OBC1与图4的△IBC相似，得到，所以路径长为15+14+13-10.5=31.5。

师：这位同学的思路清晰流畅，解法自然，一气呵成，这是经常积极参与、深刻思考所获得的学习能力。受这位同学的启发，有没有同学能提供新的解题思路？

生：由题意可知△O3O1O2与△ABC有相同的内心I，分别作出它们的内切圆。

如图5，易证O1O2∥ BC，O2O3∥ CA，O3O1∥AB，所以△O3O1O2∽ △ABC，得到13）=31.5。

图4

图5

师：这位同学沿着“前人的足迹”，灵活运用相似三角形的周长比等于相似比，轻松求解。还有不同的解法吗？

生：我们小组的意见是构造半角的三角函数。

师：很好！请你代表小组，到台前说说解题思路。

生：为便于观察关系量，可以分解图形如下：

图6

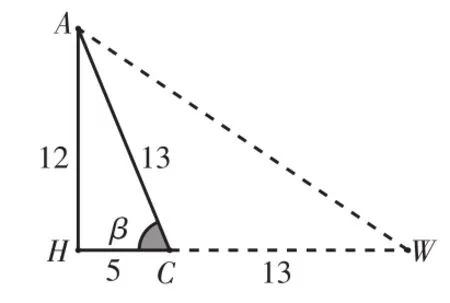
图7

图4中，BC边上的高AH将△ABC分割成两部分，得到直角三角形AHB、AHC。设∠ABH=α，6、图7，此时易得

师：这组同学通过构图，将半角的三角函数巧妙地“创造”出来，这种“图形智造”产生的效果是明显的，更是神奇的。这就是思维的延展性和生长性，我们必须为这个小组点赞！以上我们欣赏到了三种不同的解法，都很精彩。下面我们换一道题，再试试好吗？

生（齐）：好的。

【问题2】如图8，O是半圆的圆心，半径为4，C、E是圆上的两点，CD⊥AB，EF⊥AB，EG⊥CO，∠COA=60°，则FG= 。

图8

师：这道题初看无从下手，再看你一定会有所发现。

图9

生：我们可以运用特定的解法——特殊图形法。如图9，假定点E运动到某一位置，使得点G与点O重合，即EO⊥CO,此时有EO=CO，△OEF≌△COD，可得EF=2，CD=FG=23 。

师：很好！还能试试其他特殊位置吗？

生：如图10，当点E运动到某一位置，使点F与点O重合，即EO⊥AO,此时EO=CO,△OEG≌△COD，可得FG=CD=2。

图10

生：如图11，当点E运动到与点A重合的位置时，此时点F也与点A重合，便能求出FG的长度。

图11

师：特殊图形法就是将图形特殊化，对动点运动到特殊位置（包括临界位置）的图形进行研究，相当于代数中的“特值法”。假如这是一道解答题而不是填空题，大家有更高明的解法吗？

生：老师您说过，大战可以搬救兵，让我们多想辅助线。

师（微笑）：是的，辅助线可以改变图形的“格局”，对图形进行创新。

图12

生：根据图中线段垂直关系的条件，可以联结半径OE，得到两个直角三角形；两个直角三角形有公共斜边，可以联想到四点共圆。如图12，由题意可知∠OGE=∠OFE=90°，因为∠COD=60°，所以∠COB=120°，∠GEF=60°，联结OE，取OE中点 I，联结 IG、IF，可得 IG=IF=OE=IE=2，所以∠GIO=2∠GEI，∠FIO=2∠FEI，即∠GIF=120°，作IH⊥FG，根据“三线合一”可得GH=HF=直角三角形IGH中，有cos30°=

生：我们小组讨论后认为，要想求线段FG的长，可添加辅助线，构造以FG为一条边的直角三角形，再运用勾股定理解决问题。

图13

如图13，根据“一中同长”得出G、O、F、E四点共圆，可得∠GFO=∠GEO，作 GH⊥OA，有△GHF∽△OGE，得出CD，有△GHO∽△CDO，得到

师：有没有小组能再一次锦上添花呢？

生：我们小组认为，G、O、F、E四点共圆，圆的直径为OE，直角三角形CDO的外接圆直径为OC，因为OE=OC，所以这两个圆是等圆，由∠COD=∠FEG可得弧CD与弧FG度数相等，所以FG=23。

师：果真厉害！你们小组繁花似锦，你就是其中最为夺人眼球的一朵！

一题多解，解法同源；一题多图，殊“图”同归。在平时的学习中，如果教师能够引导学生善于发现，善于归纳，数学思维之花就能永不凋谢。“独学而无友，孤陋而寡闻。”课堂需要每个人的独立思考，但更需要集思广益，需要小组合作的头脑风暴。这样，学生的思考才会更深刻，思维才能更自由，这也是成长课堂的价值所在——让每一个生命个体都能健康、快乐地成长。