基于复杂网络的股票市场相关性研究

陈 帅

（上海理工大学 管理学院，上海 200093）

一、引言

金融系统是一个典型的被众多因素影响的复杂系统的看法，已经是许多学者的共识。近年来，统计物理中的各种概念和方法被广泛应用到金融系统中，并且取得了许多成果。对于金融物理研究方向的学者而言，金融市场是一个动态系统，股票市场中包含着大量的历史金融数据，因此股票市场是研究金融市场的一个热门方向。

股票市场间的互相关系数网络是由股票市场的收益率序列的相关系数矩阵构造而成，互相关系数矩阵是金融物理用来描述金融市场状态变化的有效工具。近年来，诸多学者运用互相关系数矩阵对全球股票市场进行研究。Lei Tan 等通过构造出一类非局部时间动态可观测模型，使用来自不同国家的25 个股票市场中的数百支股票探测过去的波动率序列和未来的收益率之间的相关性，得出无论对各股还是股指过去的波动率序列对未来股票收益率有持续性影响的结论。Fang Yan Ouyang 等应用经验模式分解（EMD）分析复杂金融系统的固有多尺度的动态行为，将每只股票的收益率时间序列分解为从高频到低频的运动的固有模态函数（IMF），并将固有模态函数分为高、中、低频三组，发现高频与中频组收益率序列的概率分布以及波动率序列的自相关系数概率分布与原序列具有相似的性质,并且中频组主导杠杆效应与反杠杆效应。Jing Liu 等通过运用时间变换参数（TVP）组合模型，从全球股票市场中提取信息来预测中国股票市场的波动率。首次探索了利用全球股票信息和时变参数预测中国股票波动并确定其经济价值。将组合策略和TVP 模型与新的解释变量相结合，丰富了股票波动预测模型。由于各股票市场对中国股票市场的动态影响，采用综合方法来提高中国股票波动性的预测精度。结果表明，TVP-HAR-RV 中位数组合模型对中国股票市场的波动率预测效果最好。M.Saeedian 等使用随机矩阵理论研究了来自不同国家的40 个股票指数的互相关系数，并利用随机矩阵（RMT）分析了这40 个股票市场指数的互相关矩阵，绘制了互相关矩阵的树状图，以使这个抽象的全球市场中的社区可见。结果表明，每个市场都是全球结构的一部分，两个市场之间的相互关系并不是独立于其他市场之间。世界金融市场由三个社区组成，地理位置相近的股票市场更容易在同一个社区内。

运用状态矩阵知识，将股票之间的相关关系通过阈值法构造出阈值网络，将构造出的阈值网络依据时间先后顺序分为三个阶段。第一阶段，1998—2004 年，第二阶段，2005—2011 年，第三阶段，2012—2018 年。运用K 均值法将股票之间的相关关系进行聚类。结果表明，股票之间的相关关系无论在哪一个阶段均可分为三类，C2 类表示的五种股票市场之间的关系，表明美国股票市场内部联系紧密，欧洲地区股票市场联系紧密，中国大陆股票市场内部之间联系紧密，这与我们平时的认知是一致的。C3 类在第一阶段把7 种股票市场的相关关系聚为一类，在第二阶段新增了台湾股票市场与日本股票市场的相关关系，香港股票市场与日本股票市场之间的相关关系。表明全球化趋势使亚洲股票市场的相关性显著增加，第三阶段与第二阶段保持一致。为了更加形象刻画股票市场之间相关性随着时间发展的变化趋势，本文将每一阶段的阈值网络汇总求均值构成平均阈值网络。结果发现，随着时间的推移，各个地区的股票市场联系的越来越紧密，欧美股票市场可以看作一个整体，亚洲地区股票市场可分为两部分，一部分是中国大陆股票市场，它外界股票市场联系不够紧密，另一部分由日本，中国台湾、香港这三个股票市场构成。

二、数据处理

收集的股票市场数据从1997 年4 月到2019年1 月共262 个月4 580 个交易日股指收盘价格序列。证券市场周末、节假日和遇到特殊情况时（如：2001 年9 月11 日发生911 恐怖袭击事件，美国证券交易所关闭至9 月17 日开始交易。）均不进行交易，于是本文选取了各只股指均开盘的交易日期作为研究的对象。本文将十个股指之间的45 种关系进行编号，如表1 所示。

表1 十只股指之间的相关关系

选取各个股票市场均开盘的交易日期股票指数收盘价作为研究对象，这使得全球股票市场的股票指数的收盘价格序列的序列长度相等，因此可以用矩阵的方式表示出来，如式（1）所示。在本文中选取的全球股票市场的股指个数为M=10，序列总长度为T+1=4580。

为了消除股指价格序列的不平稳性，分析不同股票市场收益率之间的相关关系。本文将股指价格序列进行对数差分处理取绝对值构成收益率的波动率序列，如式（2）所示。vi，t表示第i 个股指在t 时刻的波动率，T 表示重新构建出的波动率序列的长度。

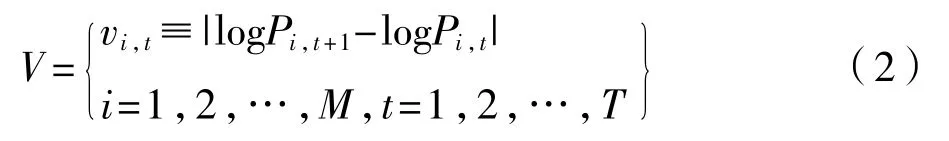
三、模型的构建

使用pearson 相关系数法求收益率之间的线性相关关系时会出现正负抵消的情况，不能很好的表示出股票市场的相关性。而使用收益率的波动率序列计算出股票市场收益率的相关性，该相关性不仅包括股票市场之间收益率的线性相关关系也包括非线性相关关系，而且巧妙地避免直接用收益率求pearson 相关系数出现正负抵消的情况。因此，本文使用股票市场的收益率的波动率序列进行模型的构建。为了扩大样本个数，指定一个窗口和步长沿着收益率的波动率序列滑动，从而切分出若干块小的收益率的波动率序列矩阵，对每一个矩阵分别用pearson 相关系数法求出股票市场之间的相关系数，对相关系数取绝对值用来表示股票市场之间的相关性强度的度量。通过阈值法将股票市场之间相关性很弱的联系剔除，从而构造出阈值网络。

（一）构建股票市场之间的状态矩阵

对于波动率序列，指定一个窗口（L）和步长（Δ）沿着序列滑动，从而形成一系列小的片段序列矩阵，每个小的片段序列矩阵可以表示为（3）式。d=1，2，…，W-1，W。d 表示以步长（Δ）沿着序列滑动所滑动的次数，W 表示以步长（Δ）沿着序列滑动最多可以滑动的次数。在本文中，以一年的交易日作为计算一次相关系数的时间窗口长度，以一个月的交易日作为步长（滚动时间窗口长度），共得到251 个窗口。

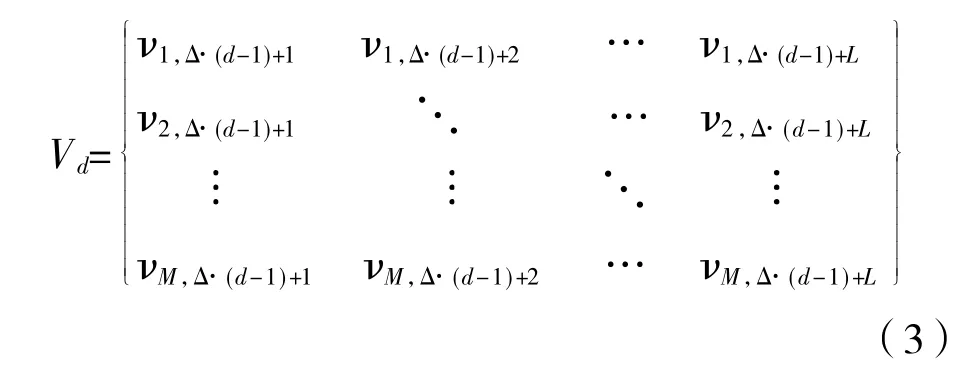
为了衡量全球股票市场在某个时间段内相互之间的相关关系强度，本文求出每个小的波动率片段序列矩阵的绝对相关系数矩阵，绝对相关系数矩阵的每一个元素可以用（4）式计算出结果。

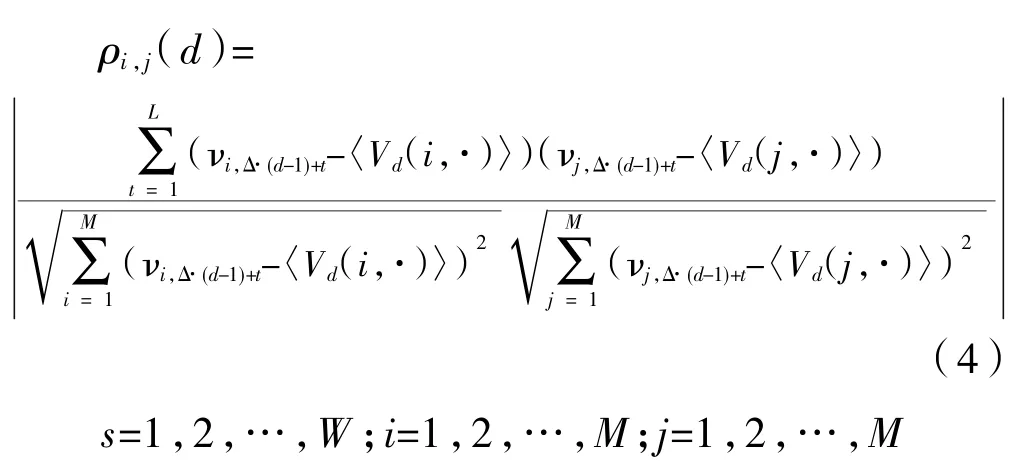
（二）选取阈值并构造阈值网络

总体的绝对相关系数涨跌趋势无法探析具体股票市场之间的相关系数强度的大小，不能排除冗余信息，导致无法抓住重要相关系数强度和结构。本文采用阈值法对绝对相关系数矩阵中较小的绝对相关系数进行过滤，删除冗余连边构建出阈值网络。在一个窗口中十支股指相互之间的皮尔森相关关系有45 种，在251 个窗口中就有11 295个相关系数。将所得到的绝对相关系数汇总，求出绝对相关系数的累计频率分布函数，通过观察累计频率分布函数的趋势可以得到，当绝对相关系数小于0.4 时，出现累计频率分布函数的斜率明显大于绝对相关系数大于0.4 的情况，因此本文选取阈值r=0.4。

通过选取阈值，可以构造出股指之间阈值网络，当绝对相关系数大于阈值的时候说明股指之间的相关性足够强，则绝对相关系数不变，反之则为0。

四、股票市场网络结构趋势分析

分布在不同地区的股票市场之间的联系不尽相同，同一地区不同的股票市场之间的相关性很强，而分布在不同地区的股票市场之间会有怎样的联系呢？本节对十个股票市场相互之间的45 种关系分三个阶段进行聚类，分别求出不同阶段的平均阈值网络。

（一）股票市场之间相关性的聚类分析

聚类分析是将数据集中某一特征相似成分聚为一类。而K 均值聚类是最著名的划分聚类算法之一。K 均值聚类算法首先随机选取K 个对象作为初始的聚类中心。然后计算每个对象与各个初始聚类中心之间的距离,将每个对象优先安置到距离最近的聚类中心。当全部对象安置完成，依据现有的对象的分配状况重新计算每个聚类的聚类中心。不断重复该过程直到每个对象的分类结果不再发生变化，聚类中心不再发生变化，误差平方和局部最小为止。

为了区分全球股指之间相关性的强弱随着时间发展的变化关系，本文选取分布在不同国家具有代表性的十个股票市场指数按照时间发展分为三个阶段：第一阶段为1998—2004 年；第二阶段为2005—2011 年；第三阶段为2012—2018 年。分别将每一阶段依据股指之间的相关性大小进行聚类。用K 均值聚类使得类内具有较高的相似度，而类间的相似度较低，从而划分出股指之间的差异。本文用ratio1 表示第一阶段组内平方与每一类的组内平方和之和的比值，ratio2 表示ratio1 的变化率。用ratio3 表示第二阶段组内平方与每一类的组内平方和之和的比值，ratio4 表示ratio3 的变化率。用ratio5 表示第三阶段组内平方与每一类的组内平方和之和的比值，ratio6 表示ratio5 的变化率。从图1 可以看出，随着k 的增加ratio1，ratio3，ratio5 逐渐减小，当k ≥3 时，ratio1 的变化率ratio2，ratio3的变化率ratio4，ratio5的变化率ratio6 均趋向于稳定。因此，本文将十只股指每一阶段的45 种关系均划分为3 类，分别表示为C1，C2，C3。

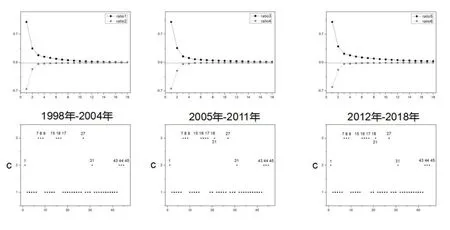
图1 不同阶段股票市场之间相关性的聚类

图1 显示了45 种关系每个阶段的类别分配，本文发现，C2 中股指之间关系的相关性最为强烈，在这三个阶段中均没有发生变化，表明中国大陆内部两个股指互关联程度高，美国内部两个股指互关联程度高，欧洲各国互关联程度高。C3中股指之间关系的相关性排名第二，随着时间的推移，在第一阶段表示DAX、FTSE、CAC 与DJI 之间的三种相关关系，DAX、FTSE、CAC 与NASD 之间的三种相关关系以及TWII 与HIS 之间的相关关系被划分为一类。在第二阶段和第三阶段C3中新增了TWII 与NIKK 之间的相关关系、HIS 与NIKK 之间的相关关系，表明欧洲与美国联系紧密，而日本、中国台湾、香港三个地区在第一阶段相关性不大，在第二阶段和第三阶段相关性有所增加。而C1 中股指之间关系的相关性排名第三，C1 中股指之间的相关性远小于C2 和C3。

（二）构造不同阶段的平均阈值网络

为了更加形象刻画股指之间相关性的变化趋势，本文将每一阶段的阈值网络汇总求均值构成平均阈值网络。在平均阈值网络中，边越粗表示股票市场之间的相关性越强，没有连接表明股票市场之间相关性很弱可以忽略。从构造出的平均阈值网络中可以看出，在第一阶段，欧洲股票市场DAX、FTSE、CAC与美国股票市场DJI、NASD联系紧密，亚洲地区股票市场比较分散，香港股票市场可以看作亚洲股票市场与欧美股票市场联系的纽带，中国大陆股票市场与外界几乎没有联系，只和德国DAX 有微弱连接。第二阶段，欧美股票市场联系依然比较紧密并且有所加强，全球股票市场连边明显增强，中国台湾股票市场，中国香港股票市场和日本股票市场三者之间的相关性显著增强，中国大陆的股票市场与其他地区的股票市场虽然有联系但相关性强度依然很弱。第三阶段，世界各国股票市场之间几乎均有联系，欧美股票市场之间联系依然紧密，中国台湾、香港，日本联系紧密，值得注意的是中国大陆股票市场与外界联系有所提升，不再是孤立的个体。

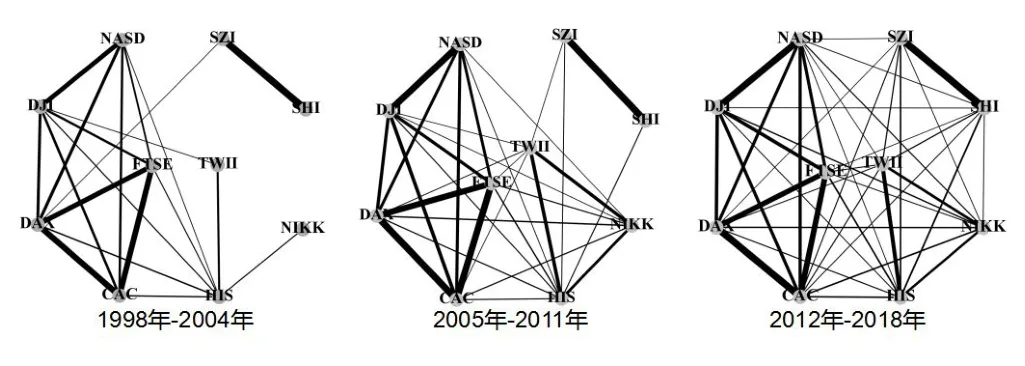
图2 不同阶段的平均阈值网络

五、结论及建议

本文通过研究分布在不同大陆的全球十个具有代表性的股票市场，DJI、NASD、DAX、CAC、FTSE、HIS、NIKK、TWII、SHI、SZI。以pearson 相关系数法为基础，运用股票市场收益率的波动率序列研究股票市场收益率的非线性相关关系。运用状态矩阵理论，将股票之间的相关关系通过阈值法构造出阈值网络，并将构造出的阈值网络依据时间先后顺序分为三个阶段。第一阶段，1998—2004 年；第二阶段，2005—2011 年；第三阶段，2012—2018 年。运用K 均值法将股票之间的相关关系进行聚类，结果发现，股票之间的相关关系无论在哪一个阶段均可分为三类且聚类结果高度相似，C2 类的五种股票市场之间的相关关系强度最强，表示出美国股票市场内部联系紧密，欧洲地区股票市场联系紧密，中国大陆股票市场内部之间联系紧密，这与平时的认知是一致的。C3 类在第一阶段把7 类关系聚为一类，第二阶段新增了中国台湾股票市场与日本股票市场的相关性，中国香港股票市场与日本股票市场之间的相关性，表明全球化趋势使亚洲股票市场的相关性显著增加，第三阶段与第二阶段保持一致。为了更加形象刻画股票市场之间相关性的变化趋势，本文将每一阶段的阈值网络汇总求均值构成平均阈值网络。结果发现，随着时间的推移，各个地区的股票市场联系的越来越紧密，欧美股票市场可以看作一个整体，亚洲地区股票市场可分为两个部分，第一部分是与外界股票市场联系不够紧密的中国大陆股票市场，在第一阶段时，中国大陆股票市场才刚刚建立，与外界股票市场之间的相关性很弱，然而随着改革开放的不断深入，中国大陆股票市场与外界股票市场之间的相关性也不断增强。另一部分是由日本、中国台湾、中国香港这三个股票市场构成的整体。在第一阶段，亚洲地区股票市场中香港股票市场与欧美股票市场连接最为紧密，第二阶段和第三阶段，亚洲地区股票市场与欧美股票市场相关性明显增强。