基于比较教学法的高等数学教学研究
2019-10-17姬玉荣刘金萌
姬玉荣,刘金萌
(1.河南理工大学 数学与信息科学学院,河南 焦作 454000;2.河南工业和信息化职业学院 基础部,河南 焦作 454000)
高等数学课程肩负着培养学生的计算能力、逻辑推理能力、分析解决问题能力的重任[1].它是理工类、经管类等专业学生的一门必修课程,是学习其他数学类课程及专业课程的重要基础.然而由于这门课程知识点多、概念抽象、计算复杂、证明灵活、应用广泛,里面渗透着大量的数学思想[2],使得高等数学课程产生教师难教、学生难学的现象.为解决高等数学教和学的难题,在教学中引入比较教学法.
所谓比较教学法,就是借助两类不同对象之间的相似性,通过比较,将一种已经熟悉或掌握的特殊对象的知识迁移到另一种新的特殊对象上去的教学方法.比较教学法的认识论根源就是思维的相似律,即客观规律在主观认识中的再现,是人类思维的一个基本规律,也是数学教学中的一种有效思维方法.事实上,很多数学问题都是在观察、总结、比较和推测中找到解决问题的方法.因此,引导学生进行比较,对于激发学生的学习兴趣,培养学生的学习、研究和创新能力,有效提高学习效率有重要的作用[3].
高等数学中的比较是多方面的,可以把同类事物进行比较,揭示事物的普遍性和特殊性;可以把不同类事物进行比较,揭示事物之间的联系和区别;可以从事物的动态过程进行比较,揭示事物的发展规律.有的放矢地进行多方面的比较,有助于人们把相似的事物区分开来,把相关的知识联系起来,获取精确、清晰的认识.
1 运用比较教学法,让学生克服学习中的畏难情绪
高等数学内容多,进度快,时间紧,任务重,很多同学有畏难情绪.在具体的学习过程中,只见树木,不见森林,无暇顾及知识体系结构的内在联系,使教学效果不理想.
为了解决学生的畏难情绪,在教学中引入比较教学法,引导学生高屋建瓴地对整个知识体系和内在逻辑形成更高层面的认识,帮助学生深刻理解高等数学知识体系的整体框架和内在逻辑.从整体上看,前七章讲一元函数微分学和积分学,后五章讲多元函数微分学和积分学.引导学生寻找极限、导数和微分这三个重要概念在教材中是按照什么样的顺序进行讲解的.不难发现,它们都是先通过实例引入,说明这些概念来源于现实生活,有很高的研究价值和研究意义,然后,给出精确的定义,由定义得到性质,重点在于如何求极限,如何求导数,如何求积分,最后,告诉大家这些概念在现实生活中的用处,给出一些用法举例.通过对上面3个重要概念的对比,得到高等数学教材中知识编排的框架结构.高等数学下册书中的多元函数极限、偏导数、全微分、重积分、曲面积分、曲线积分这些重要的概念都是按照实例—概念—性质—求法—应用,这样的方式展开的.从一元到多元、一维到多维、有限到无限、离散到连续的各种对比[4],帮助学生建立了完整的知识体系框架.
通过比较归纳,学生会发现高等数学的知识点并非杂乱无章,而是有章可循.对高等数学整个知识体系及其内在联系有了清晰的认识,对具体内容的学习方法有了明确的思路,学生普遍反映高等数学不再难学了.
2 运用比较教学法,掌握高等数学中的重点概念
高等数学中概念多且抽象难懂,教学中要花费很多时间讲解概念,但最终效果仍然不理想.经过长期摸索实践,引入比较教学法,比较概念间的联系和区别,从现象到本质、全方位地加深对概念的理解和认识.
2.1 一元函数极限和二元函数极限的概念
极限是高等数学中最重要的概念,导数和积分都是极限,因此深刻理解极限概念,对能否学好高等数学有着至关重要的作用.在掌握了一元函数极限的定义后,通过运用比较教学法,学习二元函数极限,见表1.

表1 一元函数与二元函数极限定义的比较

2.2 一元函数导数和二元函数偏导数的概念
导数是高等数学中的重要概念,是高等数学教学中的重点内容.掌握导数的实质是学好高等数学微分学的基础.
从表2可知,无论是一元函数的导数还是多元函数的偏导数,本质上都是一个极限.但从表达形式上看,又有不同的地方.二元函数对自变量x的偏导数定义中,分子部分另一个自变量y没有发生变化.二元函数对一个自变量x求偏导数时,相当于把另一个自变量看作常数,这样就完全转化成了一元函数的求导问题.一元函数导数和多元函数偏导数形式上虽然差别很大,经过比较可发现两概念间的本质联系.
高等数学中还有许多概念可以进行比较,比如数列极限和函数极限,一元函数极值和二元函数极值,一元函数微分和二元函数微分等,通过比较,寻找异同,抓住概念间最本质的联系和区别,从而对概念有更深刻的认识.

表2 一元函数导数和二元函数偏导数的比较
3 运用比较教学法,突破高等数学中的难点
高等数学中的积分包括定积分、二重积分、三重积分、两类曲线积分和两类曲面积分,积分类型多,表达形式复杂,是教学中的难点.它们之间的关系更是困扰学生学习的绊脚石.运用比较教学法,可有效突破教学中的难点.
3.1 5种积分宏观比较
高等数学中积分概念多,抽象难懂,对5种积分从引入实例、积分实质、积分域和计算4个方面进行比较,见表3.

表3 不同积分的比较
表3中把学过的几种积分放在一起,比较它们的异同.在引入时所用的实例各不相同,但是它们的实质都是一个极限,都是通过大化小、常代变、取极限这3个步骤得到的极限.它们的积分域不同,导致它们是不同的积分类型.二重积分、三重积分、曲线积分和曲面积分的计算都是要化为定积分来计算.通过宏观比较,对5种积分有了整体的认识.每种积分如何化成定积分,如何确定每个积分的上下限,这就需要进一步做更细致的微观比较.
3.2 两类曲线积分的微观比较
对两类曲线积分进行微观比较,见表4.

表4 两类曲线积分的比较
表4从定义、联系和计算3个方面给出了两类曲线积分之间的关系.两类曲线积分之间可以互化,它们都可以转化为定积分来计算,但是具体转化的过程又不完全相同,对弧长的曲线积分在转化为定积分时要进行3个代换,要把x,y,ds都化成关于参数的部分,并且化成的定积分中下限一定小于上限.对坐标的曲线积分在化为定积分的过程中,只需把x,y化成关于参数的表达式,但是有方向,所以定积分的下限不一定小于上限.通过对比,对上述两类曲线积分有了清晰的认识,既找到了相同的地方,又找到了不同之处.
3.3 两类曲面积分的微观比较
以3.2同样步骤,对两类曲面积分进行微观比较,见表5.

表5 两类曲面积分的对比
通过上述的宏观和微观比较,对积分已经有了比较清晰的认识.
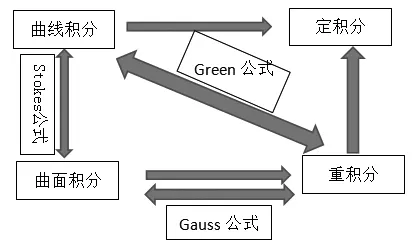
图1 各种积分之间的关系
3.4 各种积分关系的比较
既然都是积分,它们之间一定是有联系的.高等数学中的三大公式把它们紧密联系在一起,通过图1给出它们之间的联系.
Green公式把曲线积分和二重积分联系起来,Gauss公式把曲面积分和三重积分联系起来,Stokes公式把曲线积分和曲面积分联系起来.通过这三大公式把几种积分联系起来,从而突破了高等数学中最困难的部分.
比较教学法在高等数学中还有很多应用,如果深入地挖掘并引导学生学会比较,不仅能提高教学效率,还能激发学生的求知欲,提高学生的创新能力.
