一类C-M型功能反应的时滞随机捕食系统的性态

严珊珊,郑唯唯

(西安工程大学 理学院,陕西 西安 710048)

捕食系统是种群生态学研究最早、理论成果最为丰硕的领域.捕食系统会受到多种因素的综合影响,除阶段结构、稀疏效应、庇护效应等因素外，还存在生物种群密度变化对其增长率存在时间滞后现象[1,2]；捕食者的功能反应，其函数也从单一食饵密度依赖的Holling I-III型，逐步变化为食饵密度与捕食者密度双重依赖的Beddington-DeAngelis(B-D)及Crowley-Martin(C-M)型等，在具有C-M型功能反应的确定性捕食系统的众多研究文献中,文献[3,4]研究了系统全局正解的存在性、正平衡点的局部和全局渐近稳定性.

考虑生物种群在其生长过程中,除了受到数量较少但强度较大的随机干扰外,大量存在的是许多较小的、独立的随机干扰的叠加,基于此类“白噪声”干扰的随机捕食系统成为近年来生物数学研究的热点领域之一[5-9].文献[10]研究了具有时滞和随机因素的捕食系统模型,利用Lyapunov函数和It公式得到了系统的正均衡态必须满足某个条件才是全局渐近稳定的.该研究仅证明了系统的全局渐近稳定性,并未考虑系统的其他性质.据此,探讨一类具有C-M型功能反应的时滞随机捕食系统的性态.构建系统模型如下：

(1)

其中，x(t),y(t)分别代表食饵和捕食者在t时刻的种群密度；b1,b2分别代表食饵和捕食者的内禀增长率；a11,a22与a12,a21分别为食饵和捕食者种群的密度制约系数及种间竞争率；τ为时滞,即τ时刻前出生的捕食者才具有捕食食饵的能力；β,γ为正常数,Bi(t),i=1,2为完备概率空间(Ω,Φ,ω)的Brown运动,Ω是样本空间,Φ是样本空间的σ代数,ω是随机事件；σi,i=1,2表示随机扰动的强度.

1 系统全局正解的存在唯一性

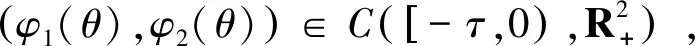
证明(Ⅰ)在t≥0上,对任意给定的初始函数

u0(θ)=lnφ1(θ),v0(θ)=lnφ2(θ),

(2)

系统(2)的系数满足局部Lipschitz条件和线性增长条件,则在t∈[0,τe)上有唯一局部解(u(t),v(t)),其中,τe是爆破时间.由It公式可知,

x(t)=eu(t),y(t)=ev(t)

是对任意给定初始函数的系统(1)的唯一正局部解.

(Ⅱ)解是全局的,即τe=+.

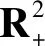
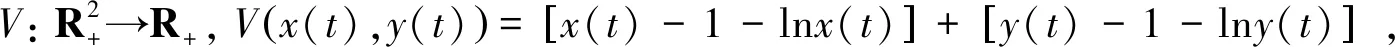
由上式可知,存在正数K,使得LV≤K,则

dV≤Kdt+σ1(x(t)-1)dB1(t)+σ2(y(t)-1)dB2(t).

上式两端从0到τr∧T(表示min(τr,T))积分并且取均值可得

EV(x(τr∧T),y(τr∧T))≤KT+V(x(0),y(0))，

对每一个ω∈{τr≤T},有

x(τr,ω)∉(1/r,r)或y(τr,ω)∉(1/r,r),

所以有

V(x(τr),y(τr))≥(x(τr)-1-lnx(τr))≥[(1/r-1-ln1/r)∧(r-1-lnr)],

或

V(x(τr),y(τr))≥(y(τr)-1-lny(τr))≥[(1/r-1-ln1/r)∧(r-1-lnr)].

则有

而

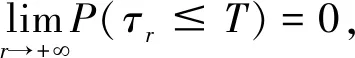
2 系统解的随机最终有界性

定义2如果对任意ε∈(0,1),存在正数M=M(ε)>0,使得对任意正初值,系统(1)的解满足

则系统(1)的解是随机最终有界.

定理2系统(1)的解是随机最终有界的.

证明对任意的正常数p,令

则对

对上式从0到t积分,并取均值可得

则存在正数K1(p),K2(p), 使得

因此

即

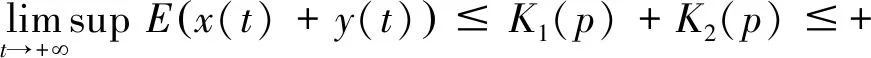
故有

所以

由Chebyshev 不等式对任意M>0,可得

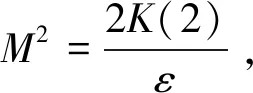
即系统(1)的解是随机最终有界的,结论得证.

3 种群的灭绝性

记

引理设x(t)∈C(Ω×[0,+),R+),则有

(1) 如果存在正的常数μ,T使得

其中，βi,1≤i≤n是常数,则

(2)如果存在正的常数μ,T和λ≥0使得

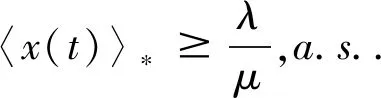
定理3设(x(t),y(t))是系统(1)的任意解,则

(1)当r1<0时,食饵种群x(t)灭绝;

(2)当Δ≜-b1a11r2+b2a21r1<0时,捕食者种群y(t)灭绝.

证明考虑如下系统

(1)令u(x(t))=lnx(t),v(y(t))=lny(t). 对u(x(t))利用It公式可得

对上式从0到t积分,再除以t得

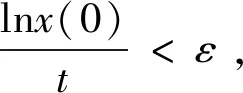
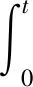
(2)同理,对v(y(t))利用It公式可得

对上式从0到t积分得

两边同时再除以t得

由于

因此，存在T1>0, 当t>T1时,

4 种群的平均持续生存性

定理4设(x(t),y(t))是系统(1)的任意解,则

(1)当r2>0时,捕食者种群y(t)平均持续生存;

(2)当Δ1≜γb1b2a11a22r1-b1a12Δ>0时,食饵种群x(t)平均持续生存.

证明(1) 对v(y(t))=lny(t)利用It公式可得

上式从0到t积分,再除以t得

因此，存在T1>T, 当t>T1时,有

根据引理可得

因此,当r2>0时,即捕食者种群y(t)是平均持续生存的.

(2)对u(x(t))=lnx(t),利用It公式可得

上式从0到t积分,再除以t得

根据引理可得

当Δ1>0时,即食饵种群x(t)是平均持续生存的.

5 结束语

考虑时滞的捕食系统受环境白噪声的影响,讨论了一类具有C-M型功能反应的时滞随机捕食系统模型.运用It公式、Lyapunov函数方法、Chebyshev不等式和随机比较定理等方法,证明了系统全局正解的存在唯一性和随机最终有界性,讨论了系统中食饵和捕食者的灭绝性和平均持续生存性.该系统模型更贴近时滞捕食种群生存实际,为降低环境白噪声对种群生存的影响、制定相应保护措施提供了必要的理论依据.