数形结合助推意义理解

邵珠利

【课前思考】

长方形是最基本的平面几何图形。它的形状比较简单，特征比较明显，长方形面积的计算方法又是其他平面几何图形面积计算方法的基础。从一年级学习“认识图形（二）”开始，学生就不断地与平面图形中的这个“老朋友”打交道。翻阅人教版教材，继三（上）学习了“长、正方形的认识”，三（下）学习了“长、正方形面积”计算后，学生对于长方形面积计算的简单题型已经有了较为扎实的基础。接下来在四（上）研究积的变化规律中，出现了解决长方形一个量不变另一个量变化求面积的问题（见图1）。

在四（下）“运算定律”的学习中，安排了在求长方形菜地面积时运用“乘法分配律”的问题（见图2）。

后续在五（上）“多边形的面积”、五（下）“长方体和正方体”、六（上）“分数乘法”、六（下）“圆柱和圆锥”的学习中又涉及有关长方形面积的内容。

但综观教材编排不难发现：自学习了长方形面积后，四（上）与四（下）教材中的两道习题编排比较分散，且都是教材已经画好图形，无须学生自己画图分析;除了在六（上）“分数乘法”学习时通过画长方形帮助分析理解题意外，运用画长方形的方法解决问题的学习几乎一片空白。

基于以上分析，笔者在三（下）“长、正方形面积”学习后设计了“画长方形解决问题（一）”，主要通过对具有“长方形元素1”的问题解决的过程，培养学生画长方形解决问题的意识和能力，在数形结合的过程中培养学生分析、解决问题的能力，进一步加深对长方形长、宽以及面积的认知。

能否跳出“长方形元素”，进一步开拓学生视野，通过画长方形解决问题的学习为学生打开另一扇窗？笔者想到在四（上）学习了“单价×数量=总价”“速度×时间=路程”这两个数量关系式后，设计了“画长方形解决问题（二）”，将不具有“长方形元素”的实际问题中的数量关系与长方形面积建立关联，进而通过画长方形，借数形结合助推对意义的理解，有效分析、解决问题。

【教学目标】

1.经历画长方形解决简单实际问题的学习过程，感受画长方形解决问题直观形象的特点。

2.在解决实际问题过程中，掌握画长方形解决问题的方法，感悟数形结合的思想。

3.感受数学与生活的密切联系，初步形成灵活运用所学知识解决简单实际问题的能力和意识。

【教学重点】掌握画长方形解决问题的方法，渗透数形结合的数学思想。

【教学难点】画长方形表达已知条件、所求问题以及根据所画长方形确立解决问题方法的思考过程。

【教学过程】

一、课前互动，营造氛围

介绍大关小学及区艺术节在大关小学申花校区举行的情况。

二、对比关联，初步感知

1.画图分析，列式解答

出示问题：在艺术节开幕式上大关小学应邀参加体操表演，每排20人。如果每排增加5人，就要增加75人。原来参加体操表演的同学一共有多少人？

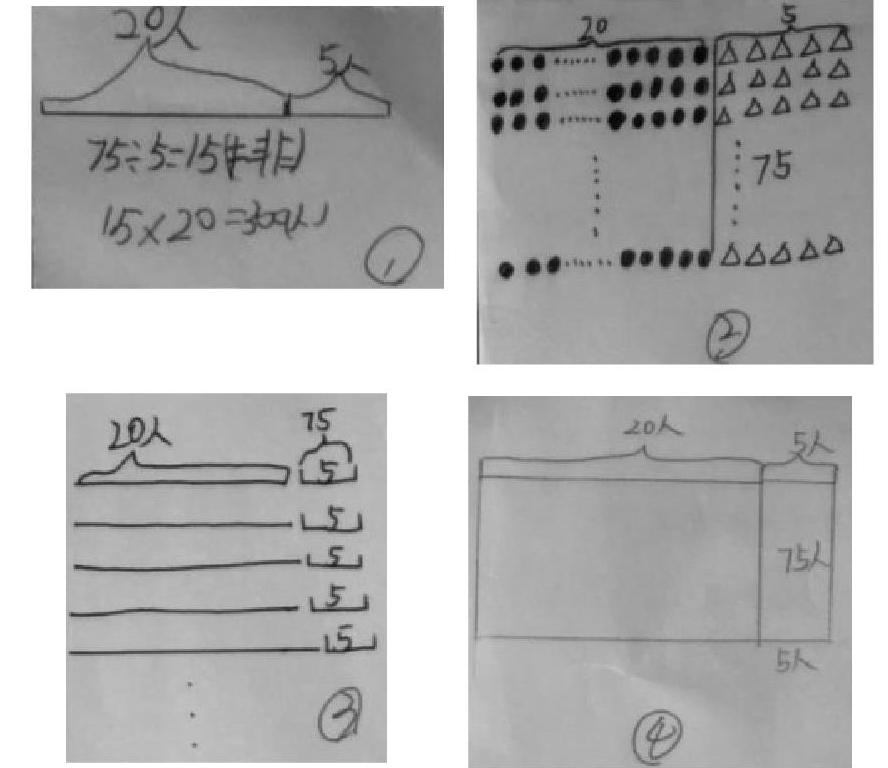
要求：（1）先画图分析，再列式解答。

（2）完成后同桌交流：你是怎么画的，又是怎么算的？

2.对比分析，感知模型

（1）四图对比，建立关联。

师：这几位同学虽然画的图形不一样，但算式都是相同的。75÷5=15（排），20×15=300（人）。

师：在这几幅图中，你更喜欢哪一幅，为什么？小组内交流你们的想法。

生：我们组喜欢第4幅图。因为它比较简洁，比较清楚。

生：我们组也喜欢第4幅图。大家看，虽然线段图比较简洁，但是不能完整表示所有信息;画圆圈图虽然比较具体，但太麻烦了;第3幅图虽然比前两幅图清楚，但还是有点麻烦;只有长方形图比较具体，能表示出所有信息，比线段图完整，比圆圈图简洁。所以我们组也喜欢第4幅图。

師：这四幅图之间有什么联系呢？

生：第1幅图表示的就是第2、3、4幅图中一排的情况。

生：第2幅图和第3幅图的想法其实是一样的，都是先表示出每排的人数（20人）;再表示排数，因为不知道具体的排数，所以两位同学都加上了省略号。最后都在刚才的基础上表示出每排增加5人，就增加75人。

生：第2幅图、第3幅图简化后就是第4幅图。每排的人数就是长方形的长;排数就是长方形的宽;总人数就是长方形的面积。

师：你们这个发现太棒了，我要把它画下来并记录下来（师在黑板上画长方形）。

（2）拓展联想，感知模型。

师：我们知道长方形的面积就是长与宽的积。通过刚才的分析，我们发现，长方形的面积还可以表示谁与谁的积？

生：每排人数与排数的积。

师：想一想，长方形的面积还可以表示谁与谁的积？

生：长方形的面积还可以表示数量、单价与总价的积。

师：你的意思就是长表示单价、宽表示数量，面积就表示总价。

生：长方形的面积还可以表示速度、时间与路程的积。

师：你的意思就是长表示速度、宽表示时间，面积就表示路程……

师：观察这些数量关系，你有什么发现？

生：它们都表示两个数的积。

师：是的，一般情况下，当表示两个数之积的数量关系时，画长方形更直观，更便于帮助我们分析解答问题。

但在画长方形时，我们一定要明确长表示什么、宽表示什么。（随着学生的回答，形成了以上板书）

（设计意图：学生对画图并不陌生，并且也比较习惯用画实物图、示意图或线段图来分析解决问题。此题信息中没有“长方形元素”，自然不存在要求学生画长方形的暗示。另外，笔者之所以没有强调要画长方形，目的就是暴露学生的原有认知。通过对四幅图形的对比分析，学生充分感知了长方形图的特点及画法，初步感受到当表示两量之积的数量关系时画长方形更直观、形象，但画的时候一定要明确长表示什么、宽表示什么、面积又表示什么。画长方形帮助分析解决问题即水到渠成。）

三、例一变式，对比画法

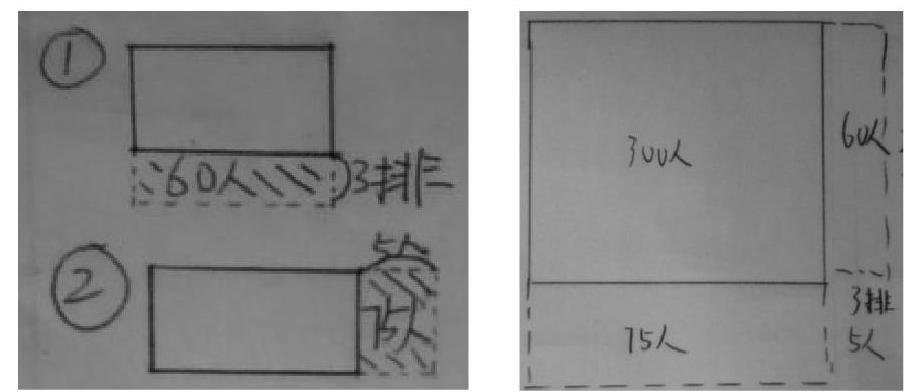
师：同学们，刚才我们不知道排数，解决了这个问题。现在每排的人数也不知道，但是知道如果增加3排，就要增加60人。其他条件不变，你还会解答这个问题吗？

要求：（1）先画图分析，再列式解答。

（2）完成后同桌交流：你是怎么画的，又是怎么算的？

（反馈讨论）

师：这两位同学画的图形不一样，你能看懂它们的意思吗？

生：第一个同学分开画两幅图，分析起来比较方便;第二位同学合在一起只画一幅图，更加简洁。

师：我们可以像第一位同学这样分开画两幅图，也可以合起来只画一幅图，都能很好地帮助我们分析问题。

师：观察图形，你发现解答这个问题的关键是什么？如何列式？

生：关键就是要求出每排的人数和排数，即求出长方形的长和宽。算式是：60÷3=20（人）——每排人数;75÷5=15（排）——排数;20×15=300（人）——总人数。

（设计意图：例1是一个量变化，画长方形图分析;而例2是在例1的基础上，另一个量也发生变化，画长方形图分析。当两个量都变化时，可以只画一幅图，比较简洁;也可以画两幅图，分析起来比较清楚。但不论如何，关键就是要明确长表示什么，宽表示什么，面积表示什么。）

四、课堂小结，明确关键

师：通过这节课的学习，你有什么新的收获？

（根据学生概括适时生成板书）

师：你认为画长方形解决问题的关键是什么？

生：明确长、宽所代表的量。

（设计意图：通过对例1和例2的回顾梳理，进一步明确画长方形解决问题的关键。）

五、图形变式，综合运用

师：接下来艺术节要进行的是合唱比赛，老师们计划给合唱团的孩子们购买一批上衣。集团校长去询问情况，两位老师是这样说的：

我去询问情况，两位老师又是这样说的：

你们能帮我和校长解答这两个问题吗？

反饋交流重点关注：

第1题强调长表示什么、宽表示什么，“降价”怎么画？

第2题强调对比分析：将画成“一增一减”与“两增”的图形进行对比分析，为什么图形不同，但得数相同？

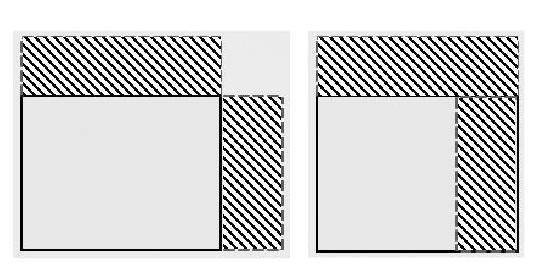
（设计意图：试一试1和试一试2的情境与例1和例2的情境不同，研究的是单价、数量与总价的数量关系;另外，画图方法也不相同，试一试1是“一减”的情况，试一试2是“一增一减”的情况。通过变换情境及改变画图方式，进一步培养学生据题画图并借图析题的意识与能力。）

六、沟通模型，积累经验

师：（同屏呈现）我们今天研究了一增、两增、一减、一增一减四种情况，但不论是哪种情况我们都需弄清楚长表示什么，宽表示什么，面积表示什么。

（设计意图：通过同屏对比，对今天所研究的四种模型进行整体感知，同时寻求共性，即画长方形解决问题的关键就是要明确长表示什么，宽表示什么，面积表示什么。同时使学生进一步感知对于研究两积关系的题目，用画长方形的方式解决问题更直观、形象，便于分析解决。）

【教学反思】

一、找准学习起点，引发有效学习

在“画长方形解决问题（一）”中，因为有“长方形元素”，所以学生自然能想到画长方形图进行分析。而“画长方形解决问题（二）”将不具有“长方形元素”的实际问题中的数量关系与长方形面积建立关联，进而通过画长方形，借数形结合助推对意义的理解，有效分析、解决问题。这对学生来说是具有挑战性的。学生最初画的线段图、圆圈图、简化圆圈图等都是对于解答队列问题积累的原有学习经验的有效提取，通过对不同图形的对比分析，不断明晰画长方形解决问题的优越性，对画长方形解决两量之积数量关系的问题也达成了共识。

二、创设优质情境，保持探究兴趣

学生是否能够进行自主学习以及自主学习投入程度如何，主要取决于教师创设的问题情境的优质与否。本课中围绕艺术节参加队列表演的人数、合唱队购买服装等实际问题展开探究，从例1变式到例2，从画一边、两边增加的长方形图到画一边减少，一边增加、一边减少的长方形图，学生始终保持较高的探究热情。情境看似不变，却又着实发生变化;图形看似相同，但的确又不相同，不相同之中又有相同之处。学生探究其中，其乐无穷。

三、 加强对比关联， 感悟画图关键

“画长方形解决问题（二）”从“一增”“两增”到“一减”“一增一减”，图式在不断发生变化。在解决这些问题时，学生不但要掌握长方形图的画法，更应明确画长方形解决问题的关键就是要确定长表示什么，宽表示什么，面积表示什么。因此笔者创设多次对比关联的学习活动，增强学生对这一关键问题的感悟，不断积累学习活动经验。

四、数形有效结合，积累活动经验

其实，画长方形图是解决问题的一种有效策略，在解决平均数问题、分数乘法问题以及一些稍复杂的两量之积数量关系的问题时，画长方形图往往会使问题变得简单易懂。

数学家华罗庚说：“数与形，本是相倚依，焉能分作两边飞。”对于解决两积数量关系的问题画长方形图更加直观、形象，有助于分析数量关系，促进学生对题意的有效理解，这彰显了数形结合的魅力。形使数更直观，解题更加有效，课堂更加精彩，在不断画图分析的过程中，经验积累更加到位。

（浙江省杭州市申花小学   310000）