基于需求调度模型对我国共享单车的调度研究——以南京市为例

高志， 聂静， 范国倩， 荀梓莹

安徽财经大学金融学院，安徽 蚌埠 233030

随着互联网的巡视发展及移动支付手段的广泛使用，共享单车数量不断增加.ofo、哈罗、摩拜等共享单车作为新型出行工具逐渐进入大众视野.因其零排放、高分布密度、高灵活性等优势在一定程度上推动了我国绿色出行方式的进一步发展.与此同时其分流了公交车人流，一定程度上缓解了城市交通压力[1].但是随着其数量的增加及分布范围的逐步扩大，共享单车行业发展也出现了诸多问题，特别是轨道交通站点周围的共享单车停放问题以及高峰客流潮汐现象带来的租赁点数量有限、停车位置固定等不均衡问题，都亟待解决.基于我国共享单车的现状，本文以南京市为例，运用多元线性回归模型、邻接矩阵模型及时空分布，统计建立车辆使用需求调度模型[2]，用车辆需求系数和周转率和推算出各地区的共享单车周转率，进而设计出20万辆单车在各个时空的调度分配模型.旨在为“公共自行车+公共交通”发展模式提供新思路，为共享单车科学调度提供理论及实践应用基础.

1 不同时空下共享单车需求量

1.1 研究思路

本文选取南京市为研究对象，因不同的人口数量和人口密度可以代表不同的区域，所以本文选取不同地区的人口数量、人口密度和时间作为自变量.先通过MATLAB软件对20万辆单车的骑行数据做时空统计，然后将时间分成5段，分别为[300，500)、[500，700)、[700，900)、[900，1100)、[1100，1300).再对数据作数据可视化处理，用MATLAB软件画图分析，将以上三个自变量对单车需求量的影响用三维立体图的形式表示出来，最后对共享单车的时空分布作出讨论，设计出需求调度模型，针对优化单车投放、对公司的经营模式进行整体规划[3].

1.2 研究方法

首先我们根据南京市人口数量和人口密度对共享单车骑行数量的影响分别做出自变量与因变量的散点图，通过判断可用多元线性回归模型.调用regress命令建立模型求解回归系数，调用命令rcoplot(r,rint)分析数据异常点的情况.在MATLAB中用rcoplot(r,rint)命令可以做出残差与残差执行区间图形.

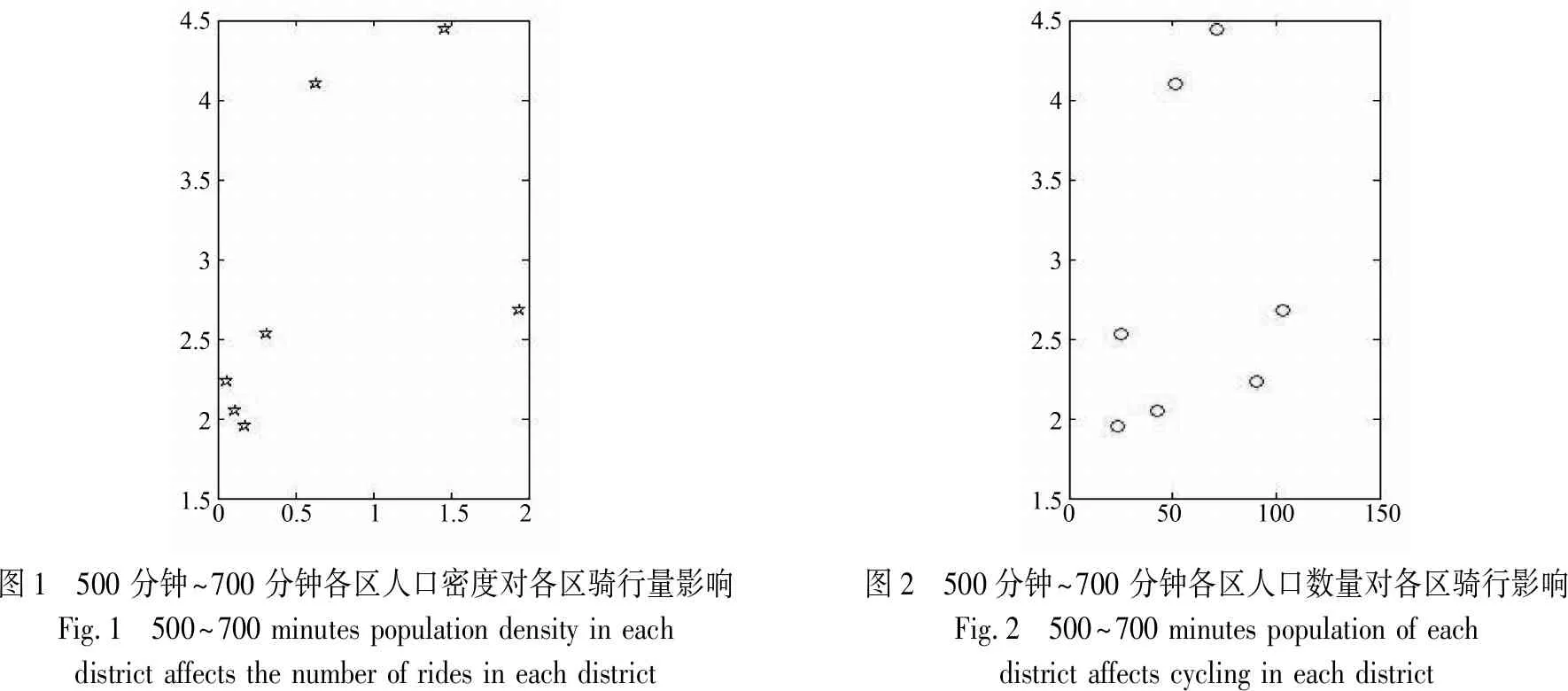
图1 500 分钟～700 分钟各区人口密度对各区骑行量影响Fig.1 500～700 minutes population density in each district affects the number of rides in each district图2 500分钟～700 分钟各区人口数量对各区骑行影响Fig.2 500～700 minutes population of each district affects cycling in each district

表1 各区域单车需求量回归分析结果(上述图中从左往右 1 至 7 个点分别代表： 玄武区、栖霞区、鼓楼区、建邺区、秦淮区、江宁区、雨花台区)Tab.1 Regression analysis results of bicycle demand in various regions(From the left to the right, 1 to 7 points in the above figure represent: Xuanwu District,Qixia District, Gulou District, Jianye District, Qinhuai District, Jiangning District, Yuhuatai District)

1.3 结果分析

对比5个残差图得出在5个时间段中，500 分钟～700 分钟这个时间段区间中单车需求量达到所有时间段所有地区单车需求量的峰值.若仅从单个残差图分析即不考虑时间因素，随着人口密度的增大，共享单车的需求量也随之增大，但增大到一定程度后单车需求量又开始递减.从空间来看，前三个地区单车的需求量基本不随时间的变化而变化，从图中看出像玄武区、鼓楼区、秦淮区比较靠近经济政治中心的地区单车需求量相应更多，而江宁区、栖霞区等稍偏一点的地方，单车需求量明显减少.

2 不同地区共享单车数量的分配方法

2.1 研究思路

首先本文选出城市中主要的八个功能区域：文教区、商业购物区、休闲娱乐区、交通服务区、居住区医疗卫生区、风景名胜区、生活服务区，并将其依次编号为1～8.其次利用MATLAB得出其不同区域的分布情况图，进而得出单车在不同地区的需求量，最终得出各个地区单车的需求量的分配方法[4].

2.2 理论准备

邻接矩阵表示法是将图以邻接矩阵(adjacency matrix)的形式存储在计算机中.图G=(V,A)的邻接矩阵是如下定义的：C是一个n×n的0-1矩阵.

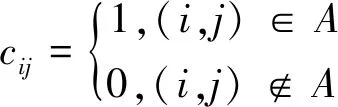
也就是说，如果两个地点之间有一条弧，则邻接矩阵中对应的元素为1；否则为0.本文从某一区域出发到一个区域最短时间用此弧来表示，在邻接矩阵的所有n2个元素中，只有m个为非零元.如果单车分配量比较分散，这种调度将浪费大量的时间，从而增加了在单车查找的时间.

2.3 研究方法

首先根据共享单车骑行数据，导入Excel 中进行整理，然后对所提供的单车骑行数据进行统计分析，从某一区域出发到不同区域的分布情况表(邻接矩阵)如表2.

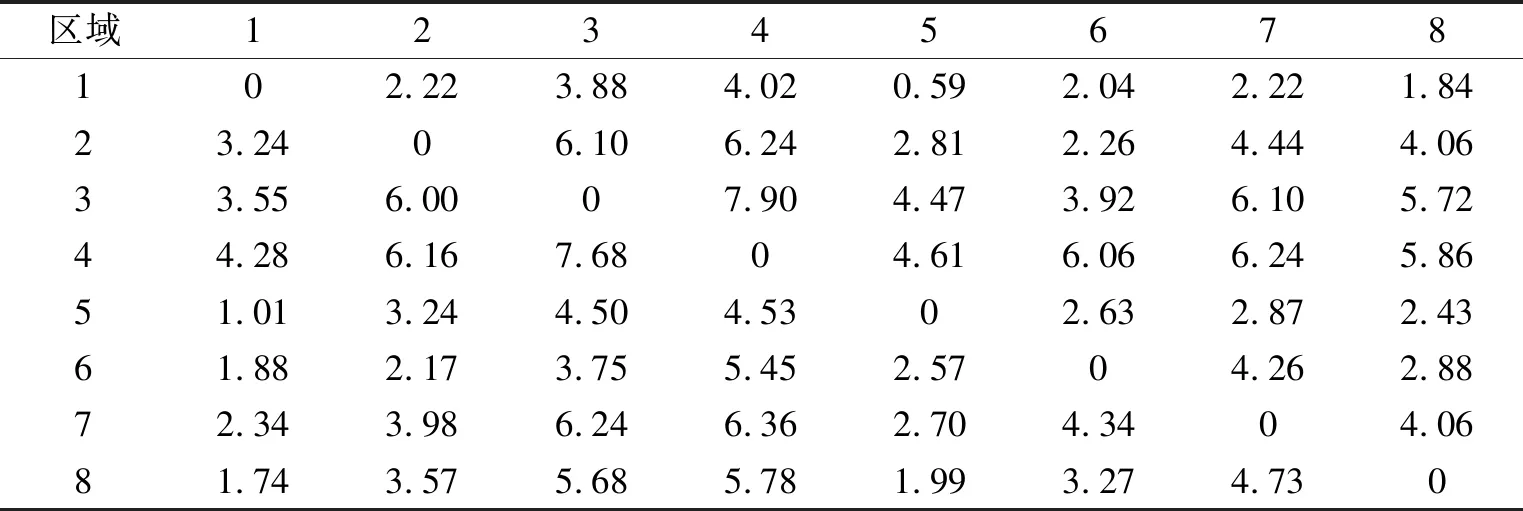
表2 从某一区域出发到不同区域的分布情况表(单位：万辆)Tab.2 Table of distribution from a certain area to different areas (unit: 10,000 units)

由邻接矩阵用MATLAB软件导出三维图(图3).

2.4 结果分析

将数据按到达地区分类，得到1到8每个地区的需求量，并计算每个地区占总需求量的比例，把20万辆车按照比例分配，可以得出分配方案如下表3.其中休闲娱乐区、交通服务区、风景名胜区所需共享单车数量占比较高，需求较大，较其他功能区应投入更多的共享单车，并加强对该功能区单车的管理[5].

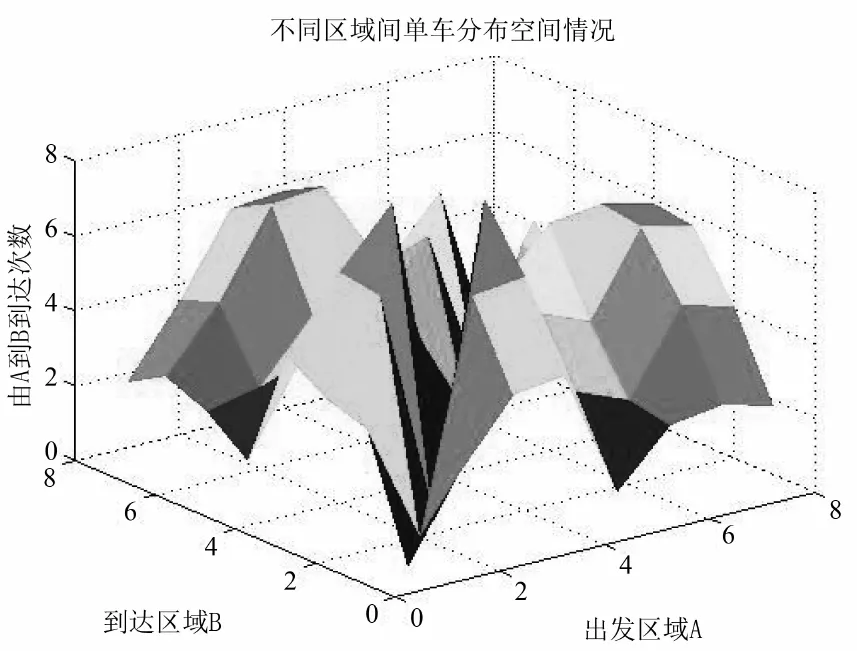
图3 不同区域间单车空间分布情况
Fig.3 Distribution of bicycle space between different regions

表3 分配方案(单位：万辆)Tab.3 Distribution plan (unit: 10,000 units)

3 基于车辆使用需求调度模型对共享单车需求调度方案设计

3.1 研究思路

首先建立车辆需求系数模型及周转率公式，并用搜集的数据计算出各地区的共享单车需求量[6].然后按照各区域需求量占总需求量的比例计算20万辆单车在各区域的调度分配.

3.2 研究方法

各时段、各区域使用车辆的需求系数K：指各时段的累计借车次数与全天总借车次数的比值.L表示借车数量，m表示区域的总数，n表示时间段的总数.

(1)

周转率是指共享单车动态需求量达到稳定状态后，某一区域的单车在单位时间内所流出量或流入量占总量的分数值.Rt表示系统时间内共享单车的借出次数，B0表示初始时刻自行车数量[7].

(2)

将时间间隔划分为3个长时间序列段：0～800，800～1 100，1 100～1 450，并分别定义为高峰期、平峰期、低峰期.在3个时间段序列内分别计算各时间段各区域使用车辆的需求系数，再根据各时间段、各区域使用车辆的需求系数公式，算出各区域分时段的需求量.由公式2计算出各区域在3个时间段的使用周转率情况.其次利用3个时段的用户量估计车辆需求数目并除以共享单车的周转率，最终得到在每个区域满足用户需求的单车数量.按照各区域需求量占总需求量的比例计算20万辆单车在各区域的调度分配方案(表4).

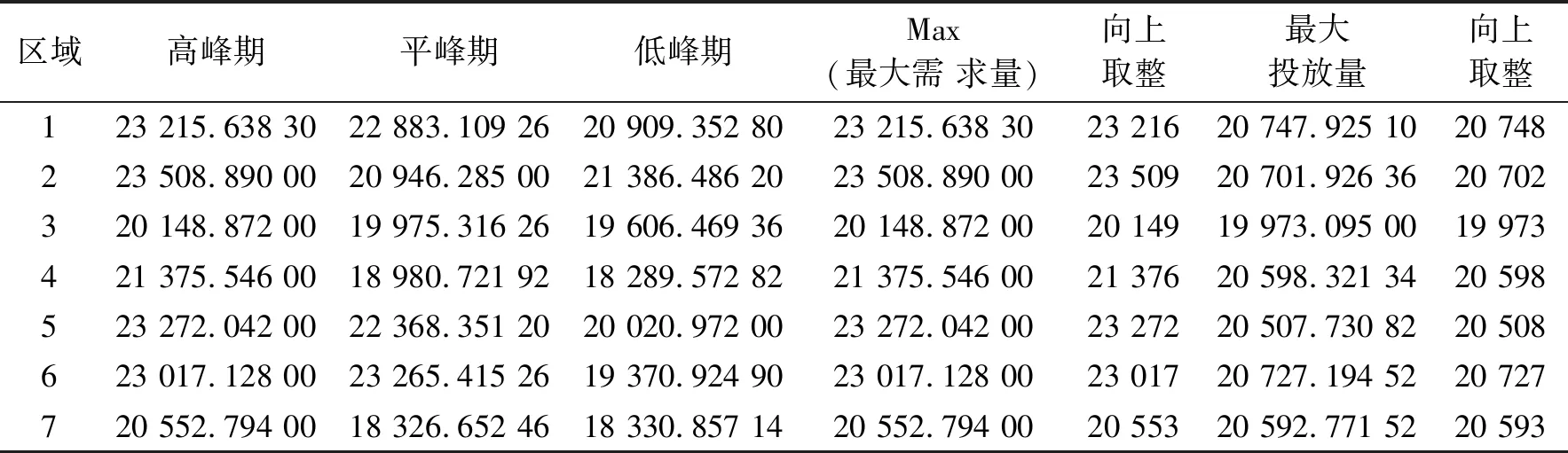
表4 分时间段各区域需求量及投放量Tab.4 Demand and volume of each region in different time periods

4 单车最优经营模式

4.1 针对公司最优分配

共享单车利润最大化是公司投放的目标，因而不得不考虑边际收益曲线[8].多数城市使用单车一次大约为0.5元～1.0元，取区域为2样本通过MATLAB绘出其投入量与利润的收益曲线.

设需求函数为q=a-bp, 则收益函数为TR=p*q=ap-bp2，MR=a-2bp=a-2b(a/b-q/b)=-a+2q为边际收益曲线方程.当MR=0时，q=a/2，此时共享单车公司能够实现收益最大化.但最优投放比例还要考虑成本最小化，这个主要考虑如何投放单车使得闲置率最低，无谓消耗最少，因而需要考虑用户的需求程度[9].

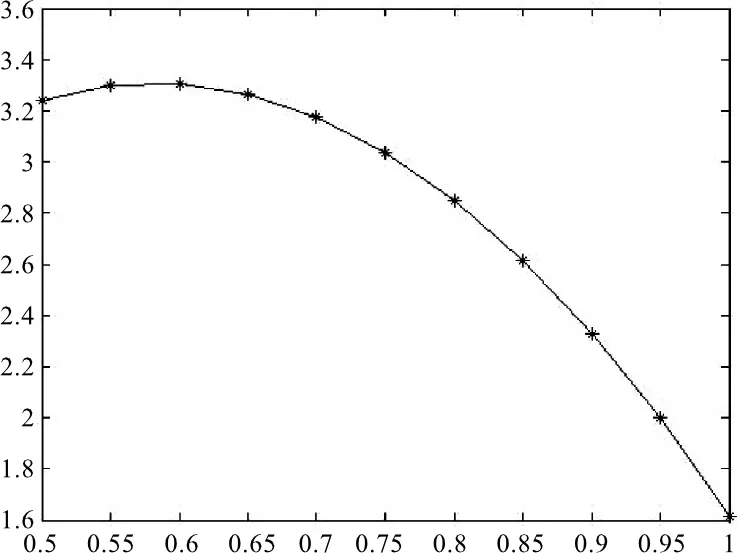
图4 收益曲线
Fig.4 Yield curve

4.2 针对用户需求的最优分配

我们将各区域的实际用户使用量与用户需求量的差值定义为用户需求满足程度[10].根据所得数据，设定基数为20万，进行差值运算，得出两者的差值如表5.

又考虑到表格数据的单一性以及其他因素对区域满意程度的影响，故引入泊松分布对概率进行求解.

因考虑到单车使用者的需求主要与车辆需求者的移动模式以及是否需要骑行有关，又因以20万辆单车为样本，n=200 000很大，且每一区域在各个时间段的总数很大，实际骑入、骑出较少，因而p较小，所以服从泊松分布.将从各区域骑出所需的单车数量，用x表示，将从各区域骑出的实际单车数量，用k表示.设各区域的实际使用为a，则

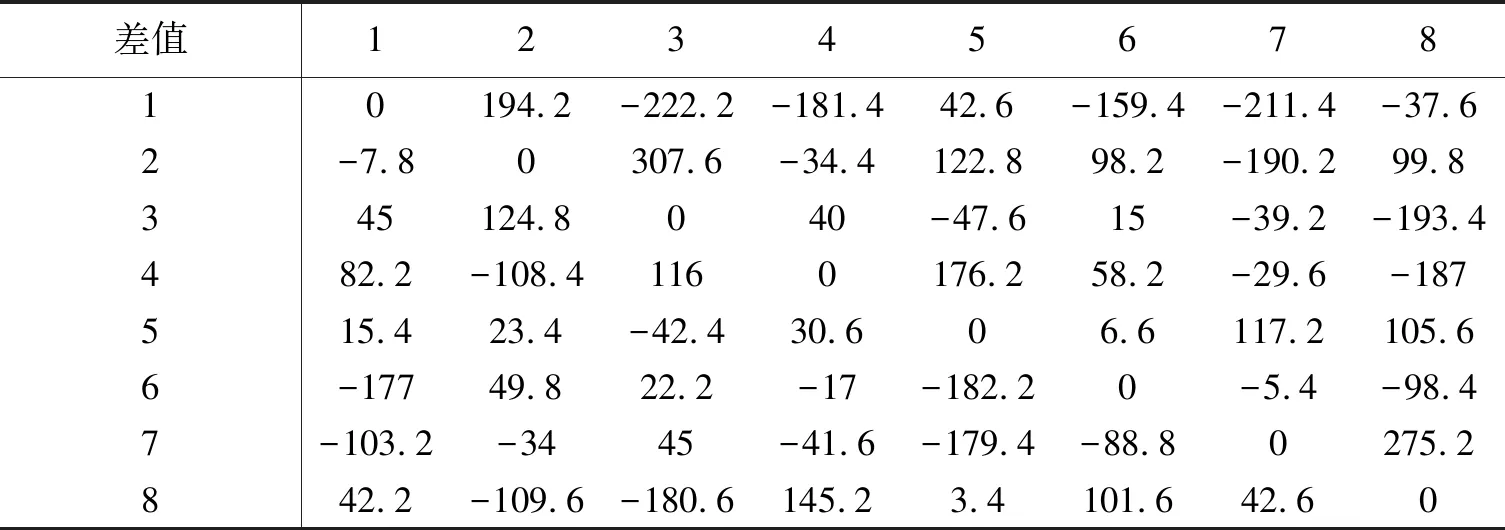
表5 各区域的实际用户使用量与用户需求量的差值Tab.5 Difference between actual user usage and user demand in each region

即a～P(λp),所以E(a)=λp为各区域的平均用车数.可以据此求解出不同区域单车使用概率(单位：%)，如表6所示.

表6 不同区域单车使用概率Tab.6 Probability of bicycle use in different regions

由假设可知，骑入到某区域的单车数量只与该区域的数量有关，因而骑入量也应作为各区域所需共享单车满足程度的衡量指标[11].据此将达标与否进行统计，得到结果(表7).

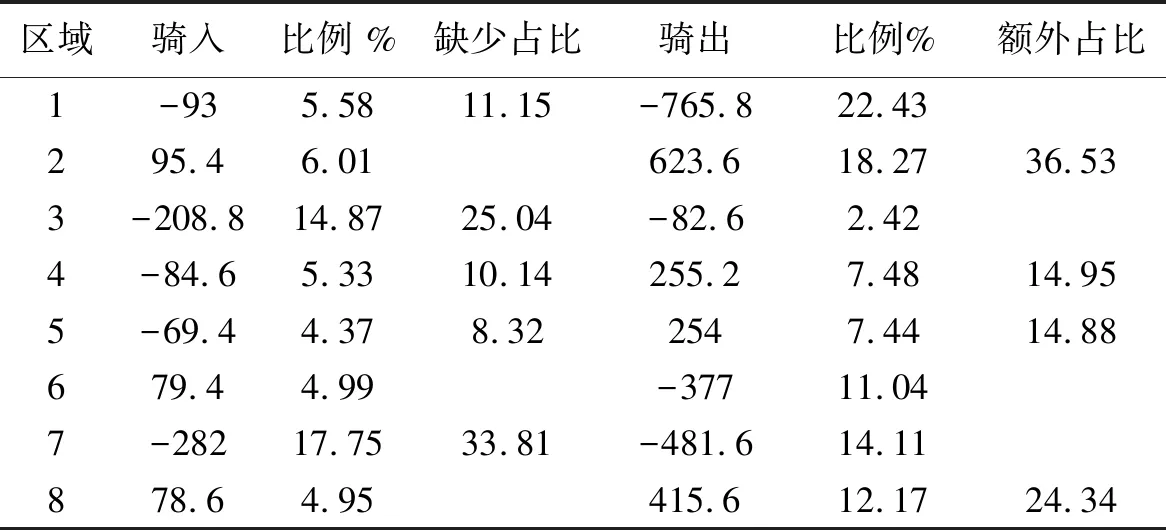
表7 单车骑出占比和缺少占比情况Tab.7 The proportion of bicycles rided out and the missing

观察表7，由上述条件可知，4区域、5区域骑入数量少且骑出数量多，应对其进行优先调度.建立以下计算公式.

再对骑入缺少占比和骑出过多占比进行权重划分，即若有100辆共享单车进行投放，可向1区域投放约4辆，向2区域投放约25辆，向3区域投放约8辆.同理，向4区域投放约13辆，向5区域投放约13辆，向7区域投放约11辆，向8区域投放约16辆.此时对厂商而言能够实现其MR=MC的利润最大化目标，对用户也是满意度最高的最优分配结果.

5 结束语

通过对共享单车需求量时间、空间的统计，找出共享单车需求量最大的区域及高峰时间段，进而针对高峰期的各个功能区共享单车投放量进行预算，为共享单车的投放量及调度问题提供指导，对优化单车的分配及提高资源利用率具有一定借鉴价值.共享单车行业可通过预算市场需求、加大宣传、提高使用便利程度、精确需求调度，逐步扩大共享单车市场，加快我国“绿色出行”前进步伐.