土工击实试验数据处理方法
2019-10-15杜瑞锋裴向军张晓超李爱君张振义
杜瑞锋, 裴向军, 张晓超, 李爱君, 张振义
(1.成都理工大学 地质灾害防治与地质环境保护国家重点实验室,成都 610059;2.内蒙古建筑职业技术学院 建筑工程学院,呼和浩特 010070;3.呼和浩特轨道投资有限责任公司,呼和浩特 010060)
0 引 言
土工击实试验是土木、水利、铁路等工程建设中用于评价土体被压实程度的室内标准试验,关系到工程质量的好坏与耐久性等问题[1-2]。因此,在生产实践、科学研究中,击实试验的重视程度比较高。尽管不同的行业规范中对击实试验的要求基本相同,但实践中有关击实试验成果整理和表现形式却达不到较好统一性和规范性。
1 击实试验数据处理方法现状
击实试验成果曲线的正确表达方式应按土工规范中的样图来绘制[3],如图1所示,曲线部分为击实数据直接绘制的,斜线部分为击实数据基础上绘制的,为土体理论上达到饱和时含水量与干密度的关系,即饱和度Sr=100%,称为饱和线或零空气线。笔者在查阅相关击实试验文献中,发现工程实践中的成果曲线整理中存在不规范的例子极多。如成果曲线图中缺少饱和线的情况[4-9];将有关击实试验数据[10]整理成图形后,发现击实曲线与饱和线出现交叉现象,表明该击实数据存在严重的错误,如图2所示。
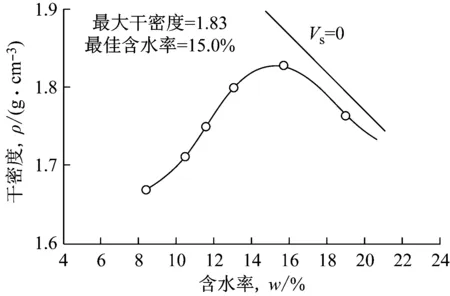
图1 文献[3]样图
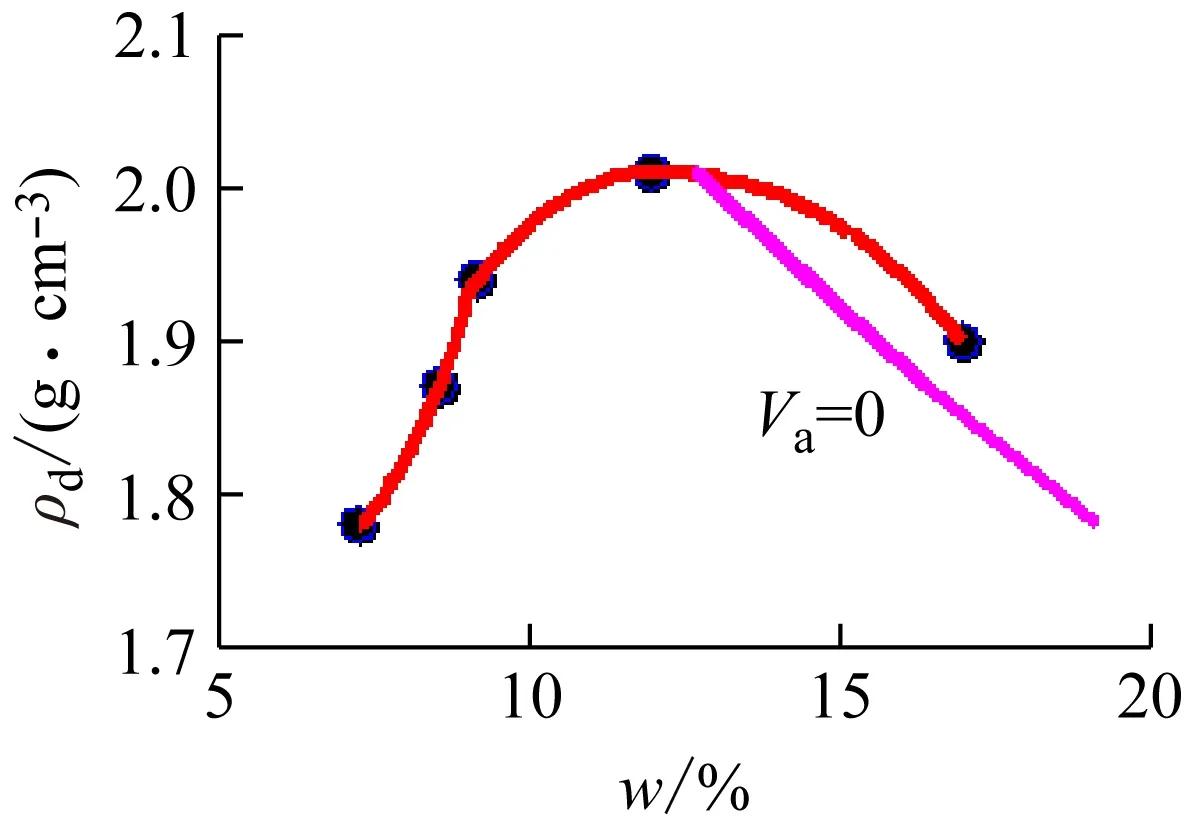
图2 基于文献[10]数据绘制的击实试验曲线
工程实践中,击实试验数据处理时确定峰值点的方法有两种。其一为图解法,但人为的随意性较大,随着计算机和数值技术的普及,已经不能适应时代的发展;其二为数值法,一般有插值法和拟合法两种。
黄英等[11]提出通过数值解法获取击实试验基本参数的思想,认为最大干密度和最优含水率之间关系符合2次函数关系,对试验数据进行拟合处理,可用于数据点不足5点的情况下的分析,但文中分析的手段不足且深入不够,且没有应用计算机程序给出处理击实试验数据的适用工具。
卿启湘等[12]指出击实数据处理存在混乱无序的问题,提出采用高次多项式拟合击实试验数据的一般性原则和方法,即在众多的n次多项式拟合曲线中,采用残差最小和最小二乘χ2分布的累计概率P较小为评价指标,来考察所选用的n次多项式是否合理的做法。该文对拟合方法的数学理论基础展开详细的阐述,但全文只讨论1个试验实例,认为3次多项式拟合效果好,没有较强的代表性,以及缺乏计算程序上的可操作性。陈进安等[13]进行了Newton插值法求解土的最大干密度和最有含水量的实践,但对插值法和拟合法的概念不清,对击实曲线峰值点的确定不够深入。
赵敏等[14]指出石灰路基土的最佳击实指标宜采用3点2次法或2次曲线拟合法来确定,且曲线拟合次数不易过高,但该文讨论的击实试验实例偏少,且应用“3点2次法”时只保留中部3个点而舍弃其他数据的做法是不妥的。
根据相关文献资料,分析和研究了击实试验数据处理的不同方法,即按照插值法、拟合法、两者兼顾的情况来分类统计,各自所占的百分比统计分布情况如图3所示。

图3 插值法及拟合法应用情况分布图
总之,以上有关击实试验数据处理研究中,应用数值法无疑是正确的选择[15-16],但目前的研究中缺乏综合性以及必要的计算机程序。本研究中,将忽略各类土本身的差异性,仅就击实试验数据的处理问题,展开有关数值插值法和拟合法适用性的讨论,并提出完整的解决方案,以期使击实试验数据处理过程更具有科学性和可操作性。
2 数值插值与拟合方法概述
数学上处理数据或函数时,基本的思想是用简单函数逼近复杂函数、用线性函数逼近非线性函数,从几何上看是以离散的点逼近连续曲线、以直线段替代弯曲弧段,数值插值法就是这一思路的最佳体现之一[17-19]。而多项式常被作为简单函数来进行相应的数值计算,其运算简便,并且随着多项式次数的增高,可以逼近任何一段光滑的函数曲线[18]。
常用的数值插值法有Lagrange、Newton、3次样条、分段3次Hermite插值法等,且插值函数均以多项式为基函数,其存在的唯一性、收敛性、插值余项(或截断误差)等在相关的论著中有详细证明过程[17-18]。
数值拟合处理的前提是肯定试验点存在一定的误差。通过构造一个函数f(x),使之能表达试验点间的关系,不要求f(x)通过所有的点,收敛条件是使得该函数与试验点间的残差(或称误差、偏差)达到最小。常用的拟合方法之一为多项式拟合,采用的准则常为最小二乘准则[17]。一般地,n个数据点,拟合多项式的最高次数为(n-1)次。
3 击实试验数据处理方法研究
利用Matlab软件编制完备的插值和拟合程序,重点分析是否存在“病态”现象、曲线的光滑程度、峰值点数值及相对误差等。该程序能完成Lagrange或Newton插值、3次样条(spline)插值、分段3次Hermite插值法程序,以及能完成2~(n-1)次多项式拟合程序(n为数据点个数)。
本研究中,共选取36个击实试验数据实例。限于篇幅,仅展示6个实例的数值分析情况,其中包括3个黄土击实试验实例、1个文献[3]中实例、1个文献[14]中实例、1个文献[12]中实例。有趣的是,拟合次数越高,多项式的拟合效果就逐渐变成插值效果,即拟合函数通过所有的试验数据点,直接说明在数值计算中,“拟合”和“插值”都是函数“逼近”的研究范畴,并以实例证实了多项式可以逼近任何函数的数学规律。
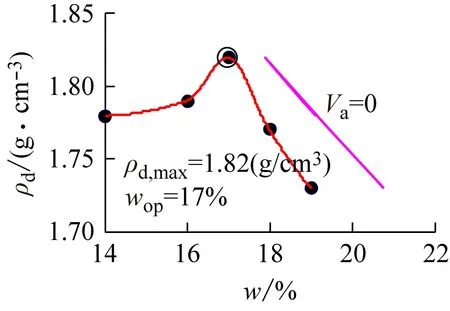
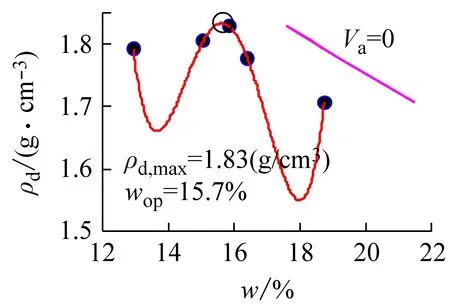
图4、5所示分别为甘肃兰州、宁夏石碑塬黄土击实试验曲线,3种方法的插值中,Lagrange和3次样条spline插值法均出现数值振荡;而分段3次Hermite插值法的效果最好;在拟合处理中,3次多项式拟合方法最好,优于2次多项式,而4次多项式出现严重的数值振荡,不再具有适用性。图6所示为陕西富县黄土的击实试验曲线,Lagrange、3次样条spline插值法稍有数值振荡,从曲线光滑程度看,分段3次Hermite的插值效果最好;在拟合处理中,3次多项式拟合方法最好,优于2次多项式,而4次多项式出现轻微数值振荡。

(a) Lagrange or Newton

(b) spline
(c) 分段3次Hermite

(d) 2次拟合

(e) 3次拟合

(f) 4次拟合
图4 甘肃兰州黄土击实试验曲线(空心圈为曲线峰值点,下同)
(a) Lagrange or Newton

(b) spline

(c) 分段3次Hermite

(d) 2次拟合

(e) 3次拟合
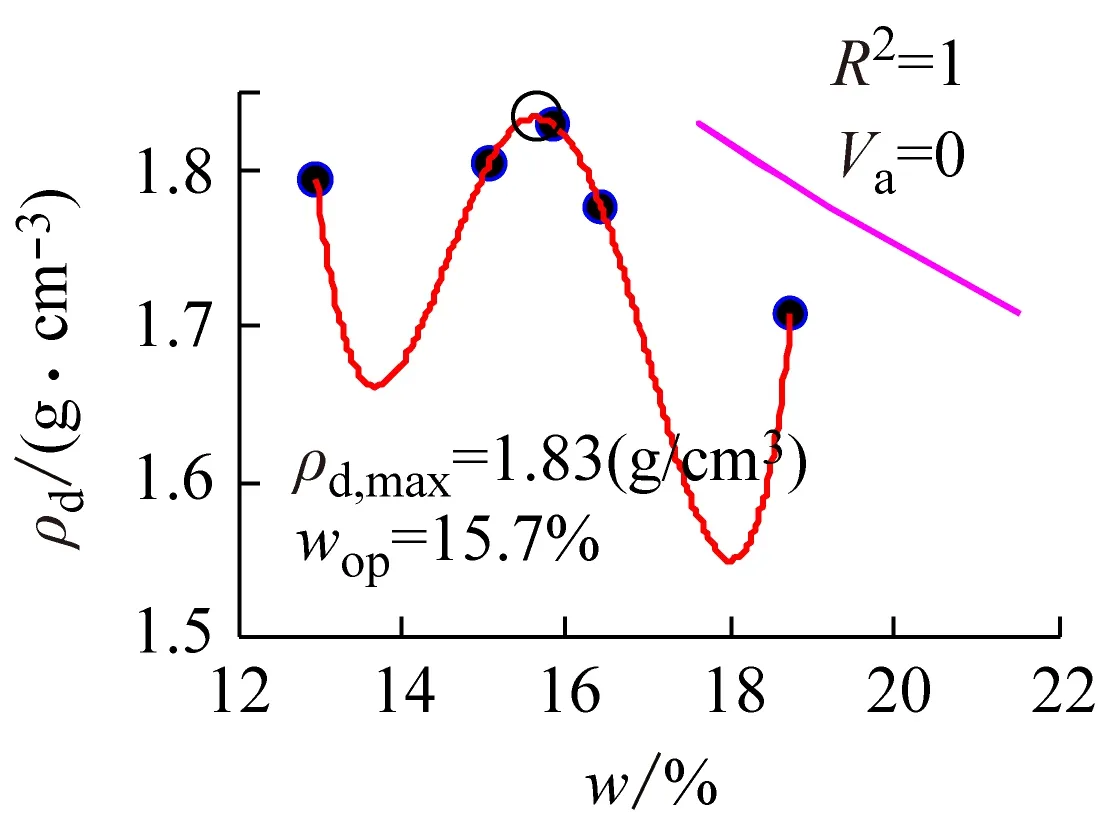
(f) 4次拟合
图5 宁夏石碑塬黄土击实试验曲线
图6所示为陕西富县黄土的击实试验曲线,Lagrange、3次样条spline插值法稍有数值振荡,从曲线光滑程度看,分段3次Hermite的插值效果最好;在拟合处理中,3次多项式拟合方法最好,优于2次多项式,而4次多项式出现轻微数值振荡。
图7、8所示分别为基于文献[3,14]中数据而绘制的击实试验曲线。由于击实试验数据较为理想,所以没有出现较严重的数值振荡,2次多项式的拟合效果稍低于3次多项式,4次多项式拟合中出现轻微的数据振荡。

(a) Lagrange or Newton

(b) spline

(c) 分段3次Hermite

(d) 2次拟合

(e) 3次拟合

(f) 4次拟合
图6 陕西富县黄土击实试验曲线

(a) Lagrange or Newton

(b) spline
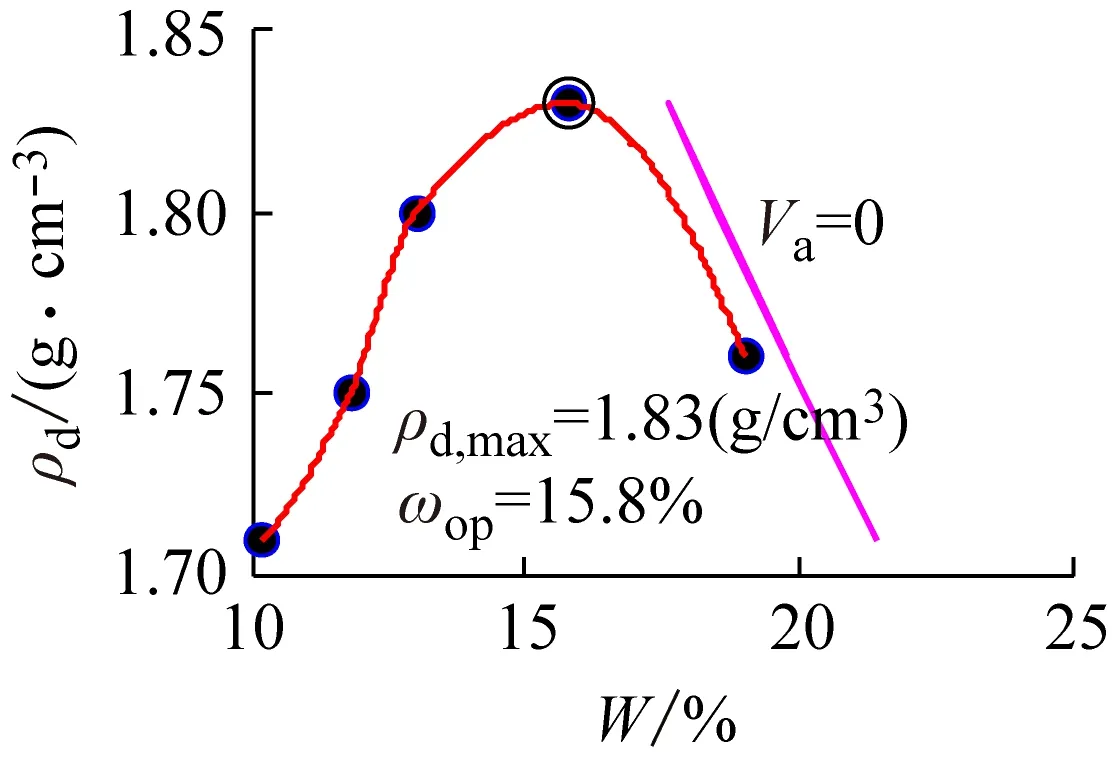
(c) 分段3次Hermite

(d) 2次拟合

(e) 3次拟合

(f) 4次拟合
图7 基于文献[3]数据绘制的击实试验曲线

(a) Lagrange or Newton
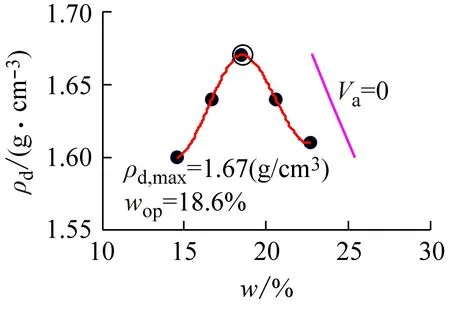
(b) spline

(c) 分段3次Hermite

(d) 2次拟合

(e) 3次拟合

(f) 4次拟合
图8 基于文献[14]数据绘制的击实试验曲线
图9中试验数据来自文献[12],3种插值方法均具有较好的光滑性,曲线的峰值点基本相同;而拟合处理中,3次拟合法中可决系数虽高于2次拟合多项式,但其出现轻微的数值振荡,整体拟合效果仍优于2次拟合多项式,同样具有轻微数值振荡的4次插值多项式,具有更高的可决系数,其峰值点的数值几乎接近插值法中数值,因本例中数据点多,故可进行5次多项式拟合。
由以上各击实试验实例的数值处理结果可知,在插值方法中,总体上讲分段3次Hermite法效果最优,能有效地消除数值振荡问题;但不能一概而论,有些实例中3次样条插值法的曲线光滑程度要优于分段3次Hermite法,如图7(b)的光滑程度要优于图7(c);而在图9中,3种插值方法中,图9(a)具有最好的光滑程度且没有出现数值振荡,说明Lagrange或者Newton在实践中也是可以采用的。因此,在插值法中,首选分段3次Hermite插值法,其次是3次样条插值法,最后是Lagrange或者Newton插值法。在拟合处理时,36个实例中3次多项式无一例外地比2次多项式更能适应击实数据的处理问题,具有更高的可决系数。而高于3次的多项式则趋向或等同于“插值”效果,失去“拟合”的意义。

(a) Lagrange or Newton
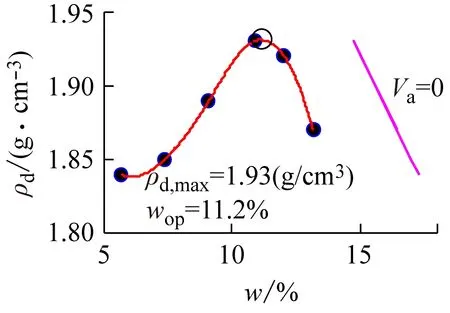
(b) spline

(c) 分段3次Hermite

(d) 2次拟合
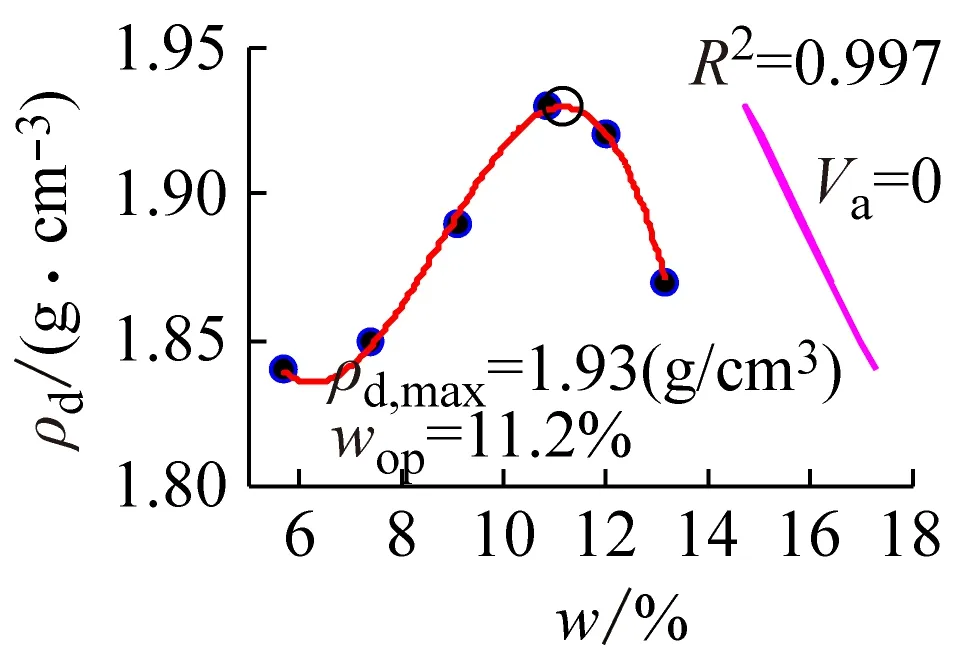
(e) 3次拟合

(f) 4次拟合

(g) 5次拟合
图9 基于文献[12]数据绘制的击实试验曲线
更值得说明的是图4~8中,(a)图为Lagrange或Newton插值后的图形,函数为4次多项式,均与各自图中的(f)图相同,函数均为4次多项式,两图能达到相同的峰值点数值,直接说明了高次的拟合函数将转变为插值函数状态;具有同样表现的还有图9(a)为5次多项式,与图9(g)表现为一样的图形,具有“殊途同归”的效果。因此高次多项式拟合在击实试验中是不适用的。最后说明一下,3次多项式拟合的适用性最好,不过在极少数的实例中,2次多项式拟合中可决系数也可达到0.9以上。
4 击实试验数据处理的建议方案
基于以上分析和研究,插值法和拟合法均可用于击实曲线试验峰值点。实践中两种方法如何选择?建议将插值法和拟合法结合起来使用,第1步使用插值法,第2步使用拟合法。总的评价标准以3次多项式拟合结果为基准(要求可决系数≥0.85),来评价3种插值方法的相对误差,以相对误差不超过±10%为限来判定击实试验结果的优劣。如果3种插值法中的任何一种的相对误差不超过±10%,表明击实试验数据可用;如果3种插值方法中相对误差都超过±10%则表明试验数据不可用,需进行补做或重做试验。将以上建议的方案以流程图方式表达出来,如图10所示。
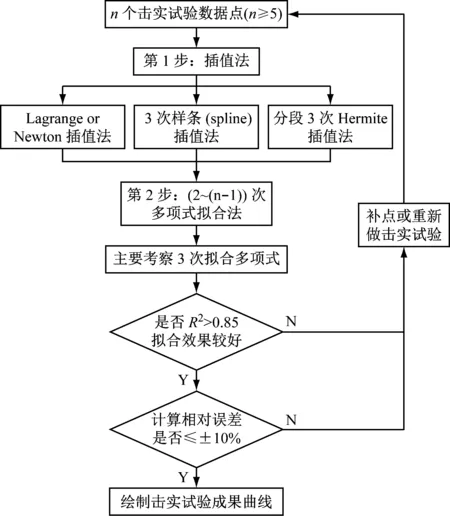
图10 建议的解决方案流程图
室内击实试验是用于指导现场填土(料)压实施工的试验,土体的压实度按下式评价:
λc=ρd/ρd max
(1)
式中:ρd为现场施工压实时实测的干密度,ρd max为室内击实试验得到的最大干密度。因此,在不同的压实度下,ρd max决定着现场施工中ρd必须达到所需的值,即ρd≥λc·ρd max。这就反映出击实试验结果的准确性将直接影响着工程质量以及相应的工程造价。
根据以上的分析,按照本文建议的方案确定ρd max的数值时,在曲线光滑度、可决系数等能满足的前提下,应优先能使ρd max具有较大值,这是对施工质量偏于有保证的考虑。
5 结 论
(1) 土工击实试验成果曲线的正确表达方式如文献[3]中的样图,即基本组成部分为试验数据点、曲线、斜线部分,以及必要文字说明部分,如最大干密度、最优含水量、饱和线等;否则,在实践应用以及科学研究中,不能称其为完整的击实试验成果曲线。
(2) 基于36个击实试验数据实例,研究了插值和拟合法的适应情况;限于篇幅,只列出其中的6个实例,3个来自笔者所在的课题组研究中,3个来自其他文献。通过分析,分段3次Hermite插值法是处理击实试验的首选方法,其次是3次样条插值法,最后是Lagrange或Newton插值法;拟合方法中3次多项式处理效果最好,而2次多项式由于其函数图形对称的特点,与3次多项式拟合效果相比,具有较低的可决系数,实践中不应采取2次多项式拟合方法;同时,高于4次的多项式拟合操作中,会因多项式的良好逼近性使拟合状态变为插值状态,也不能做为拟合函数使用。
(3) 室内击实试验是用于指导现场压实施工质量控制指标的室内试验,本文提出的解决方案有待于实际施工中进一步检验其适用性。
(4) 击实试验是基本土工试验之一,就其击实能量、试样制备方法、试样类别等而言具有复杂性。目前学者们从不同的路线进行研究,如基于改进击实设备[20]、现场压实机械[21]、非饱和土强度理论[22]、评价指标改进[23]等的研究路线,结合实践中压实路基或坝基等工程开展了大量的且使用现代多种科技测量手段的研究,有一定的创新性;但如何使击实试验数据处理过程及结果体现更高的科学性、可操作性等仍然是科研、生产实践中最基本的研究工作,同时基于Matlab软件开展的数值计算及可视化应用等应当引起工程界足够的重视。目前进行的诸多研究仍不足以解决击实试验数据在数学上的分布规律,因此有待于将室内试验、现场试验及理论分析结合起来进一步研究。
