电网故障的正余弦诊断方法

熊国江， 张 靖， 何 宇

(贵州大学 电气工程学院，贵阳 550025)

0 引 言

快速准确地诊断出电网故障的元件是实现智能电网自愈的基础[1]。国内外学者就该问题开展了大量的研究工作，提出了多种诊断方法，包括专家系统、粗糙集、神经网络、Petri网、优化技术等。其中，专家系统故障诊断方法可以充分利用专家的经验知识，但知识的维护和更新较为困难，故障容错性差；粗糙集故障诊断方法通过属性约简可以有效提高故障容错性，但对电网结构变化的适应性较差；Petri网故障诊断方法透明度高，但故障容错性有待进一步加强。与上述方法不同，优化技术故障诊断方法的数学模型理论性强，模型构建简单，是一种应用前景良好的故障诊断方法，近年来得到了快速发展。该方法先根据电网元件、保护和断路器之间的逻辑关系构造一个反映实际报警信息与期望报警信息之差的数学模型，将故障诊断问题转化为一个0-1整数规划问题，然后采用粒子群优化算法[2]、蜜蜂群算法[3]、差分进化算法[4]、生物地理学优化算法[5]等优化技术求解该规划问题，从而找到最能解释各个保护和断路器的动作行为的故障假说。近年来,优化技术的快速发展,有力助推了该方法的应用研究。

由“没有免费的午餐”理论[6]可知，没有任何一种优化方法能在电网故障诊断问题上永远保持最优，因而有必要挖掘更多可求解电网故障诊断问题的优化方法，探讨其在该问题上的可行性和有效性，丰富电网故障诊断的求解思路。正余弦优化算法(Sine Cosine Algorithm, SCA)[7]是近年来提出的一种新的智能优化算法，采用正弦函数与余弦函数完成迭代运算，其设计遵循简单、快速的原则，算法无需额外调节的参数，从而提高了应用的便利性，已在很多问题[8-14]上得到了广泛应用。

本文将SCA算法应用到电网故障诊断中，根据电网故障诊断问题的特点设计了二进制SCA算法，并采用不同类型算例从不同角度验证了该方法的优化性能。实验结果表明，与遗传算法GA和粒子群算法PSO相比，SCA算法可以快速获得更加准确的诊断结果。

1 电网故障诊断数学模型

电网故障诊断问题在数学上可描述为如下典型的0-1整数优化问题：

(1)

式中:D表示故障区域内可能故障元件数；Si为第i个元件的故障状态，1表示故障，0表示完好。

电网故障后，继电保护系统中的相应保护将会动作，断开相关的断路器，从而隔离故障元件。通过分析这些保护和断路器的动作行为可以诊断出故障元件。基于优化技术的电网故障诊断就是寻找最能解释各个保护和断路器的动作行为的故障假说。其目标函数[5,15]为：

minF(S)=

(2)

式中：r和C分别表示保护和断路器；*表示期望状态；m、p、s、mal和dir分别表示主保护、近后备保护、远后备保护、失灵保护和方向元件；∑⊕的计算规则为：累加数≠0，取1，否则,取0;wm、wp、ws、wmal、wdir和wc为权值，取值分别为0.9、0.8、0.7、0.7、0.85和0.95[5]。

2 二进制SCA算法

2.1 基本SCA算法

SCA的设计遵循简单、快速的原则，每个个体可表示为，i=1,2,…,NP，NP为种群规模。SCA的迭代过程仅仅依据下式所示的正弦函数与余弦函数实现：

(3)

(4)

式中:P=[p1,p2,…,pD]为最优个体；r1随机分布于(0,1)范围内;r2随机分布于(0,2π)范围内;r3随机分布于(0,2)范围内。

SCA在迭代过程中，采用一个(0,1)范围内的随机数r4来选择式(3)或(4)，流程如下：

初始化种群X=[X1,X2,…,XNP]

计算种群所有个体的目标函数值

初始化迭代次数t=1

While终止判据未满足do

通过目标函数值确定最优个体P

fori=1 toNPdo

ford=1 toDdo

生成随机数r4

ifr4<0.5 do

采用式(3)更新xi,d

else

采用式(4)更新xi,d

end if

end for

end for

计算所有更新个体的目标函数值

t=t+1

End while

2.2 二进制SCA算法

本文采用sigmoid函数实现实数编码到二进制编码的转换，其方式如下：

(5)

转换规则为：

(6)

式中，rand(0,1)表示(0,1)之间的随机数。

3 基于二进制SCA的电网故障诊断流程

采用二进制SCA求解电网故障诊断问题的流程如图1所示。首先确定停电范围，停电范围内的设备均列为可能故障元件，然后按照式(2)构造这些可能故障元件对应的目标函数，最后采用二进制SCA进行优化求解，从而诊断出故障元件。

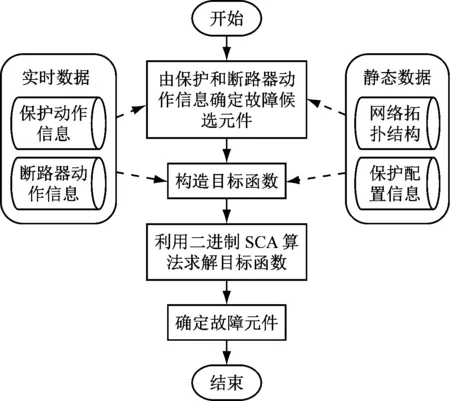
图1 基于二进制SCA的故障诊断流程

4 算例分析

4.1 测试系统

本文采用如图2所示的电力系统作为测试系统。

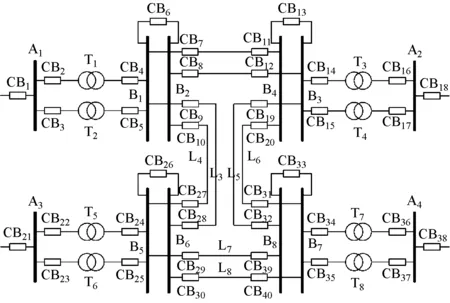
图2 测试系统

为了测试SCA的优化性能，采用GA和PSO进行对比，分别计算100次。仿真实验条件：3.70 GHz CPU，8 GB内存，Matlab R2010b。对于所有算法，NP=10，最大迭代次数Tmax=50。采用文献[5，15]中的6个故障算例来检验SCA算法的故障诊断能力，如表1所示。

4.2 故障诊断准确性结果分析与比较

表2为3种算法在6个测试算例上的诊断结果。由表可知，SCA均能100%正确诊断出故障元件，而GA和PSO均存在错误诊断的情形。由比较结果可知，SCA在诊断准确性方面优于GA和PSO。

表1 测试算例

表2 故障诊断准确率比较

部分算例(算例1、3、5)的收敛曲线如图3～5所示。由图可知，SCA具有良好的全局快速收敛特性，而GA和PSO存在不能有效收敛的情形(如算例1和算例5)，这也从另一角度说明这两种算法存在错误诊断的情形；虽然GA和PSO在算例3上能有效收敛，但收敛速度均滞后于SCA。此外，从图中还可知，故障复杂度越大(如算例5)，SCA的优势越明显，说明SCA算法在处理复杂故障情形方面具有较强的能力。

图3 算例1收敛曲线

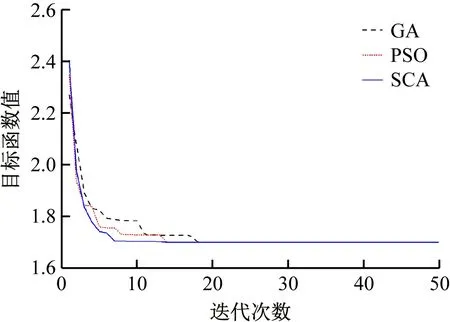
图4 算例3收敛曲线

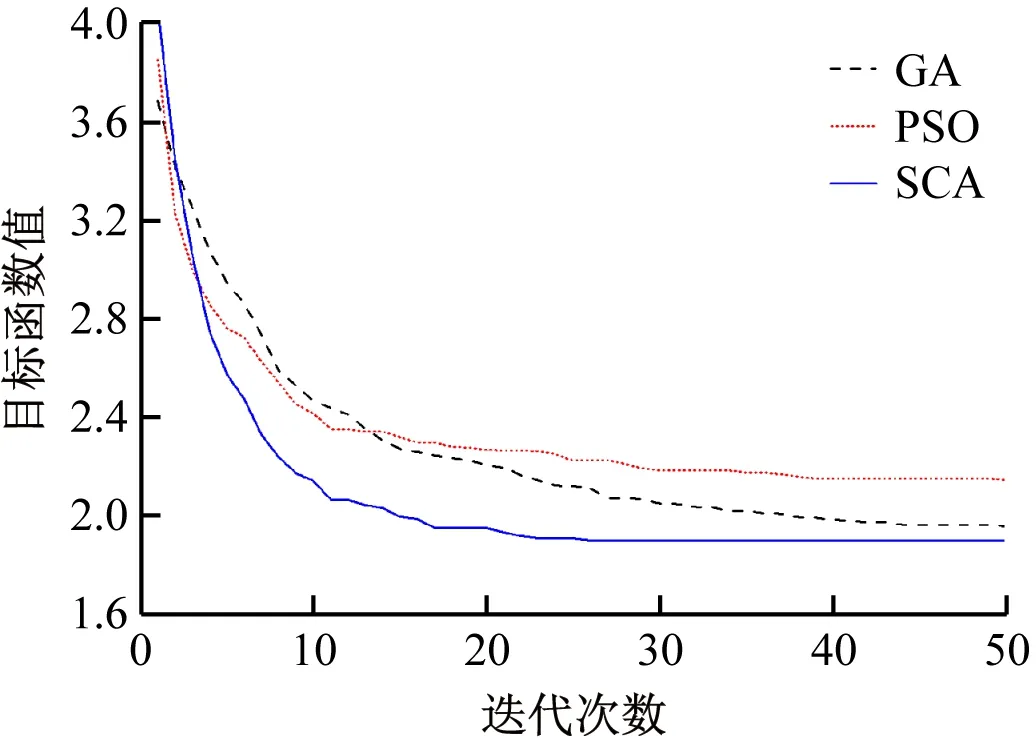
图5 算例5收敛曲线

4.3 故障诊断快速性结果分析与比较

由表3可知，SCA的诊断速度最快，比PSO快8.3%～32.0%不等，而比GA快22.7%～93.9%不等。可知SCA在诊断快速性方面也明显优于GA和PSO，这也正是SCA遵循简单、快速的设计原则的结果。

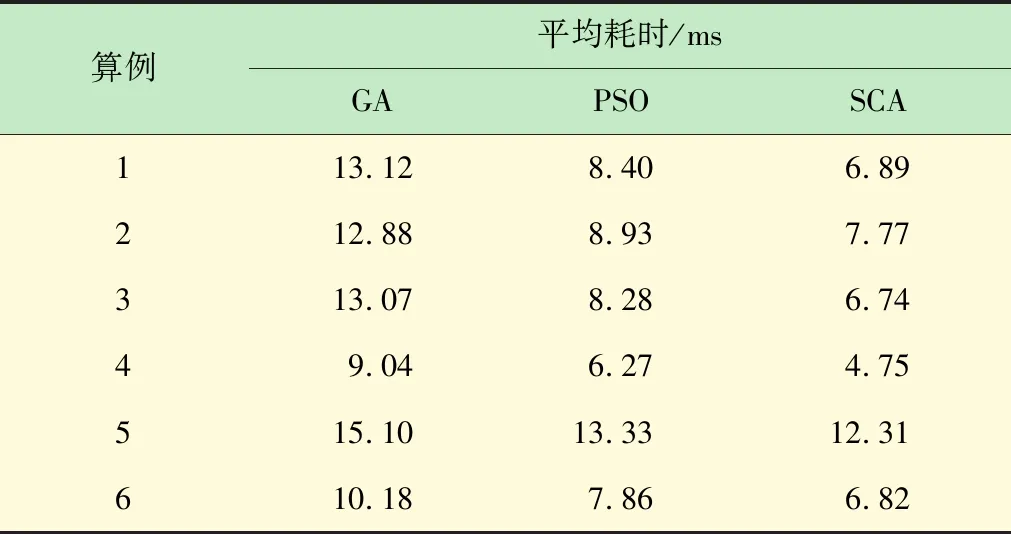
表3 故障诊断快速性比较

4.4 算法参数影响分析

SCA的一个主要特点是除了需要设置种群大小和迭代次数这两个所有智能优化方法都需要设置的参数外，没有额外需要设置的参数。虽然如此，由SCA的基本流程可知，该算法主要受随机参数r1和r3的影响，其中r1为缩放因子，主要控制算法步长;而r3为指引因子，主要控制最优个体的参与度。

(1) 随机数r1的影响分析。根据r1的特点设计了5种随机取值方式：① (0,0.1)；② (0,0.5)；③ (0,1)；④ (0,5)；⑤ (0,10)。采用最复杂的算例5对各种分布方式进行分析，结果如图6所示。由图可知，SCA的确受随机数r1取值的影响，r1取值太大或太小均不利于算法的诊断性能。究其原因，是因为r1作为缩放因子，用于协调SCA的全局探索(exploration)能力和局部开发(exploitation)能力。r1越大，exploration能力得到提升，同时也降低了SCA的收敛速度；r1越小，exploitation能力增强的后果是使SCA易陷入局部寻优，发生早熟。上述仿真结果表明，虽然r1采用随机方式生成，但随机范围的选取需要综合协调exploitation与exploration，两者尽量达到平衡。

图6 参数r1影响结果

(2) 参数r3的影响分析。针对r3设置了3种随机取值方式：① (0,2)；②(0,1)；③(1,2)。同样采用算例5进行分析，其结果如图7所示。由图可知，r3也同样影响SCA的诊断性能。当r3为(0,1)时，最优个体P的参与度较弱，SCA搜索的方向性不强，收敛速度较慢；r3为(1,2)时，P的参与度较强，SCA容易陷入局部极值；r3为(0,2)时，可以有效平衡P的参与度，从而实现explitation与exploration的有效协调。

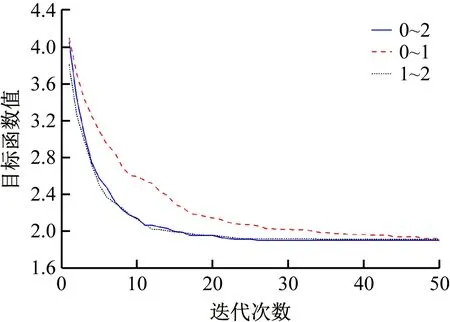
图7 参数r3影响结果

5 结 语

本文将SCA算法应用到电网故障诊断问题中。采用不同类型故障算例从准确性、快速性、收敛性等角度来验证该诊断方法的有效性。仿真结果表明，SCA算法可以快速有效处理多种复杂故障情形。SCA算法的缩放因子和指引因子均会影响SCA的诊断性能，合理的随机数生成范围的选取可以有效平衡全局搜索和局部搜索。下一步将采用正交学习策略、参数自适应等方法进一步提高SCA的优化性能，并用于求解经济调度问题。