贫预混火焰动力学及稳定性分析

2019-10-15王博涵孙潇峰胡宏斌聂超群

燃气轮机技术 2019年3期

王博涵，孙潇峰，姜磊，胡宏斌，聂超群

(1. 中国科学院工程热物理研究所先进燃气轮机实验室，北京 100190；2. 中国科学院大学，北京 100049; 3. 青岛海尔日日顺物流有限公司，山东青岛 266101)

针对燃气轮机污染物排放严重的问题，国际民航组织 (ICAO) 以及航空环境保护协会 (CAEP) 均推出了一系列严苛的排放法规。为了满足法规的要求，贫预混燃烧技术应运而生，其旨在降低燃料的比例，同时使燃料以及空气在进入燃烧区域前进行充分的混合。该技术取得了很大的成功，大大降低了污染物的排放，但其自身也存在一些缺陷，其中便包括了容易诱发热声不稳定。热声不稳定是系统的声学振荡、流体动力学脉动以及火焰热释放脉动三者的耦合造成的，其极具破坏性，可能会毁坏燃烧室表面以及限制稳定运行的范围。因此在现阶段的燃烧室设计等过程中，研究者希望能够对稳定性进行分析。火焰对来流扰动的响应，即火焰动力学，是热声稳定性分析的关键因素，而我们通常采用火焰传递函数 (FTF) 来描述火焰动力学。

火焰传递函数可以通过不同的方法获得，大部分研究通过实验得到FTF。但由于实验耗财耗力，且针对一些较为复杂的配置进行实验较为困难，同时随着电脑技术的不断发展，一些研究者开始采用CFD模拟，其中包括了稳态或非稳态模拟结合频谱分析等方法。本文采用了大涡模拟结合系统辨识的方法，原因是相比于频谱分析，其具有可以通过单一CFD模拟获得一定范围频率内的火焰响应，减小计算量的优点。

火焰传递函数会被很多不同的因素影响，大部分研究是通过改变入口温度、入口压力或当量比来观察FTF差异的。Huang和Yang等[1]在实验和数值模拟上分析了贫预混轴向旋流燃烧器中火焰结构从稳定状态向不稳定状态的转变。观察到随着入口混合物温度的增加，稳定的V形火焰转变为了非稳定的M形火焰。这种转变是由于入口温度的增加，导致火焰速度的增加造成的。然后，火焰闪回，穿透外部再循环区，稳定在外剪切层。Foley等[2]同样研究了入口温度和当量比对火焰形状的影响，观察到了相似的形态转变。在他们的研究中，也观察到了其它火焰形状，如抬升火焰或仅稳定在外剪切层的火焰。Freitag等[3]研究了压力对以天然气为燃料的预混旋流火焰传递函数的影响。研究中测试了0.1～0.5 MPa五种不同的压力。在较高的频率下，随着压力的增加，可以观察到相移。这种效应是由于强烈燃烧区的位置变换造成的。在较低频率时，随着压力的增加，火焰振幅减小，但在较高频率时，趋势正好相反。Cheung等[4]研究了压力对预汽化航空发动机喷射器的贫预混火焰传递函数的影响。研究比较了常压和1.5 MPa的压力条件下的火焰传递函数，发现在低频情况下，1.5 MPa 压力时的振幅小于常压时，而对于高频情况，趋势相反。Kim等[5]研究了常压下不同当量比的贫预混轴向旋流火焰响应。观察到在相同的入口速度和混合物温度下，通过增加当量比，火焰可以由V形转变为M形。随着参数的增加，火焰速度和反应率将会增加，火焰在内外剪切层中均可稳定。除了上述因素，燃料中掺混氢气以及不同火焰筒限制同样会对火焰的响应产生影响。

本文在后面的章节中，首先介绍了火焰传递函数、LES/SI方法、计算模型、计算工况并进行了数值验证，然后针对燃料掺氢以及不同火焰筒限制进行了火焰动力学辨识分析，之后采用低阶网络模型进行了稳定性分析，最后进行了总结。

1 数值模拟

1.1 火焰传递函数 (FTF)

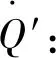
(1)

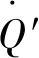
(2)

(3)

FTF的振幅被定义为：

(4)

相位定义为：

1.2 LES/SI方法

系统辨识被认为是一个“黑匣子”，在输入和输出信号的基础上，重建系统动态特性。在本研究中，Wiener滤波被用来识别UIR的不同系数hk。c=Γh称为Wiener-Hopf公式，Γ是自相关矩阵，c是互相关向量：

(6)

(7)

之后通过Wiener-Hopf公式的逆转，得到UIR系数向量：Γ-1c=h。

在进行火焰传递函数辨识的过程中，首先是对系统进行大涡模拟。在得到统计稳定的解之后，采用激励信号在入口处的平均流上叠加带宽速度扰动对系统进行激励。火焰传递函数的研究通常限于低频范围内(低于1 000 Hz)，因为大部分火焰在高频时的响应较小。

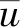
(8)

1.3 计算模型

选取某型燃气轮机的燃烧室作为计算对象，该燃烧室包括带有8个叶片轴向旋流器和中心体的燃烧器以及方形火焰筒，如图1所示。入口段直径为42 mm，燃烧器长度为90 mm，中心体直径为18 mm，火焰筒边长为84 mm，长度为127 mm。经控制网格质量后采用约500万的非结构化网格进行计算。

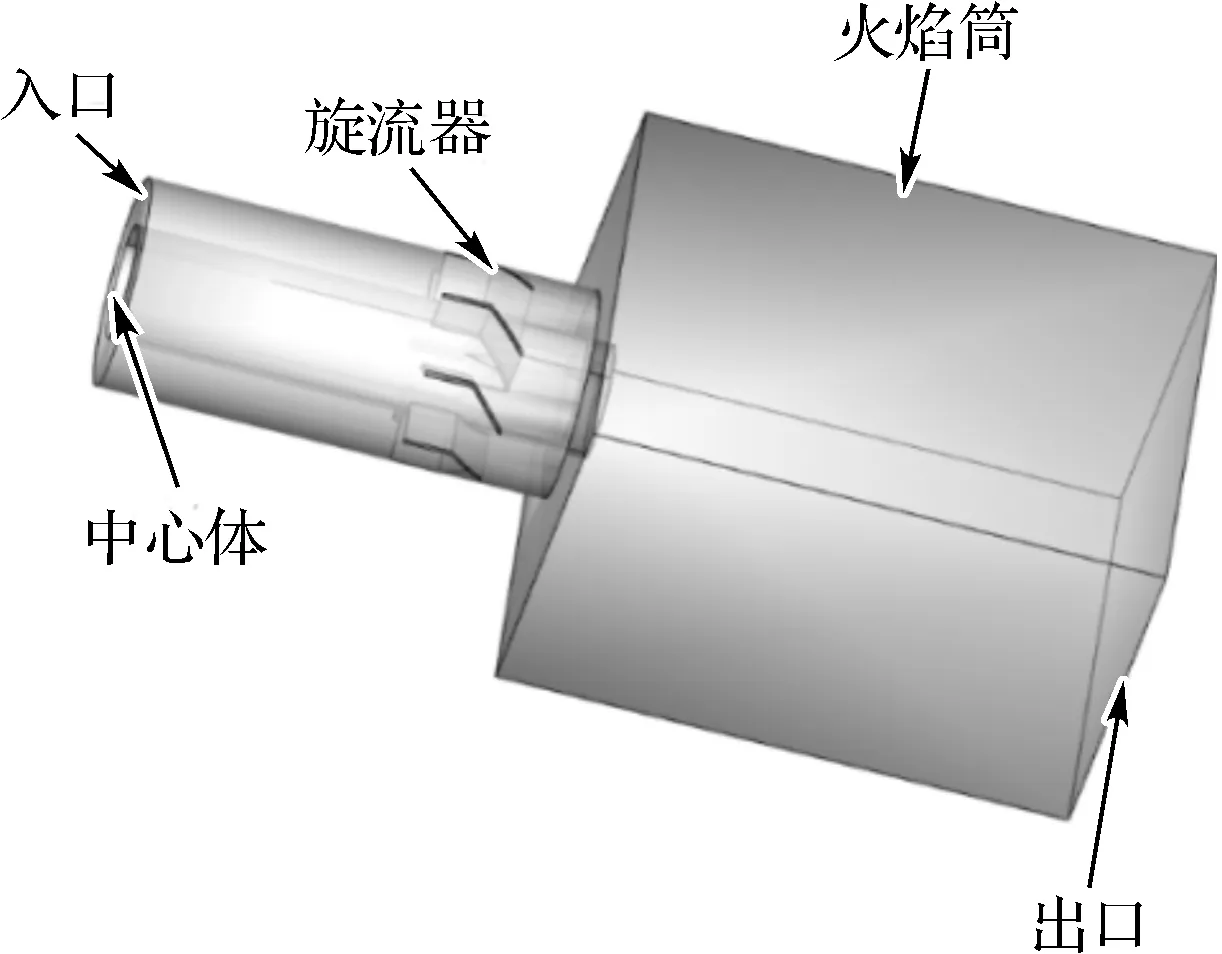
图1 燃烧室几何模型

1.4 计算工况

本文采用FLUENT软件进行计算。首先利用RANS计算初始流场，选择可实现的k-epsilon模型求解平均混合分数为0.04的燃料空气混合物。近壁处理采用可扩展壁面函数。组分模型采用部分预混燃烧。得到稳定的流场后，接着采用LES进行计算。亚格子尺度模型采用WALE模型。模拟的时间步长为0.000 1 s，每个时间步的最大迭代次数为20。入口设定为速度入口，气体速度为15 m/s，温度为600 K，出口类型为压力出口，回流过程变量设定为1，壁面设定为固定标准无滑移，通过设定燃料掺氢为10%或20%，以及不同的火焰筒横截面积，对燃烧室内流动进行CFD计算分析，来获得甲烷掺氢以及不同火焰筒限制下的火焰传递函数。

1.5 数值验证

为了验证该数值方法的可行性，针对一没有旋流器的锥形火焰燃烧器，采用完全相同的模型设置，计算得到传递函数振幅，并与Cuquel等[6]基于火焰面积变化的G方程题出的数值分析火焰响应模型的结果进行对比，结果如图2所示。对比表明，在研究较为关心的中低频段内，CFD计算与数值分析模型的结果几乎贴合，即所采用的大涡模拟结合系统分析的方法可以较好的计算火焰传递函数。

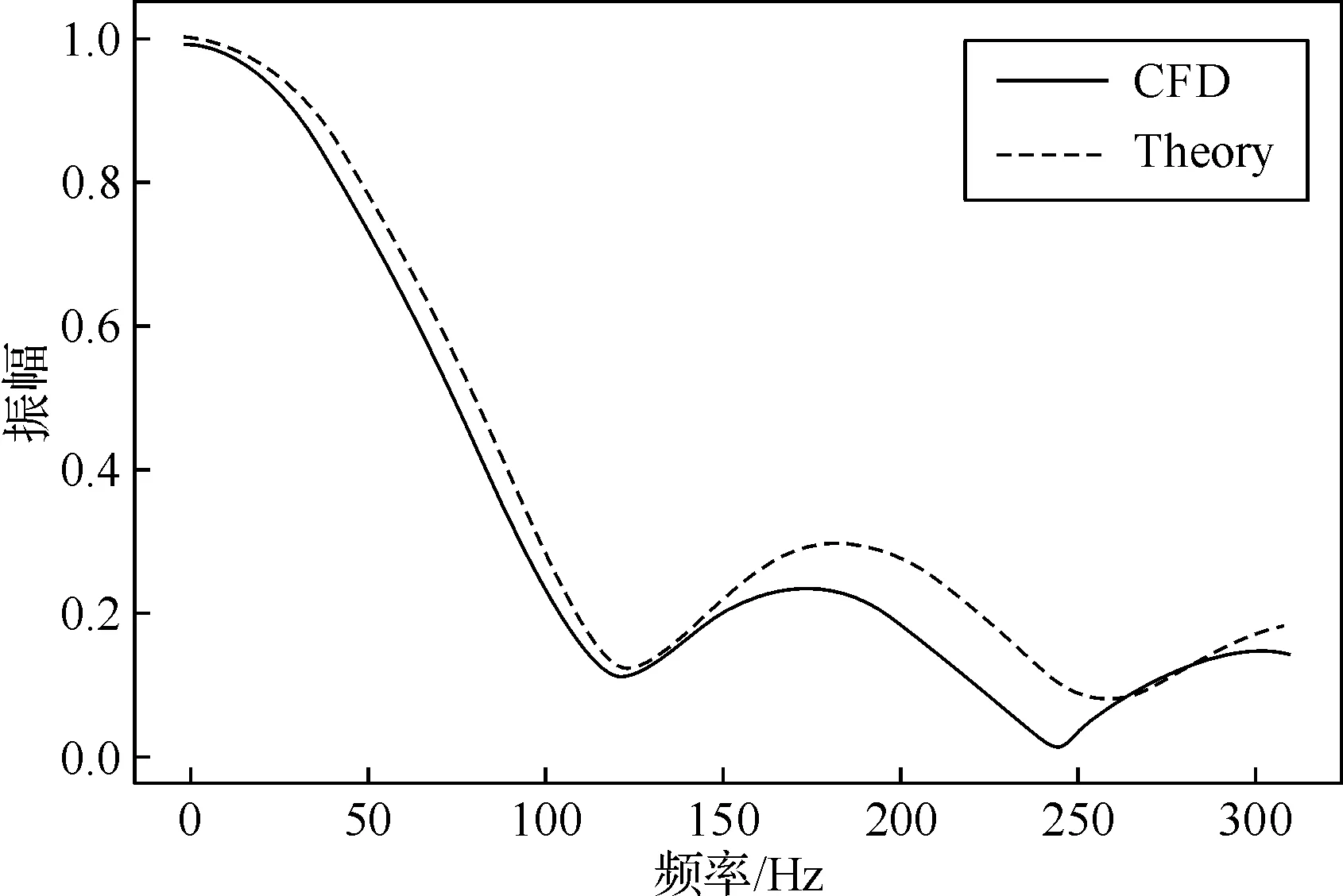
图2 CFD计算与数值分析模型对比

2 火焰动力学分析

2.1 燃料掺氢对火焰动力学的影响

由于氢燃料层流火焰速度更高、稳定极限范围更宽以及更清洁等特性，因此现阶段甲烷掺氢也越来越受到重视。本节针对甲烷中掺混不同含量的氢燃料进行了计算分析。

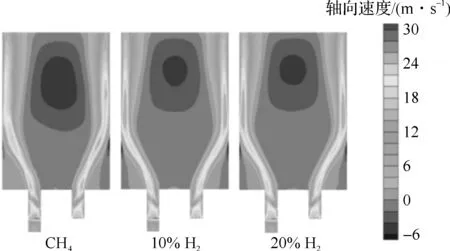
图3 不同氢含量的轴向速度场

图3为不同氢含量下的轴向速度场。可以看出，加入氢气后，由于氢气自身更高的层流火焰速度，使得火焰速度明显增大，同时回流区向下游移动并明显减小，最大负速度区减小。同时由于氢气更高的密度热值，当氢气含量增加时，从图4的温度场也可以观察到火焰温度增加的情况。

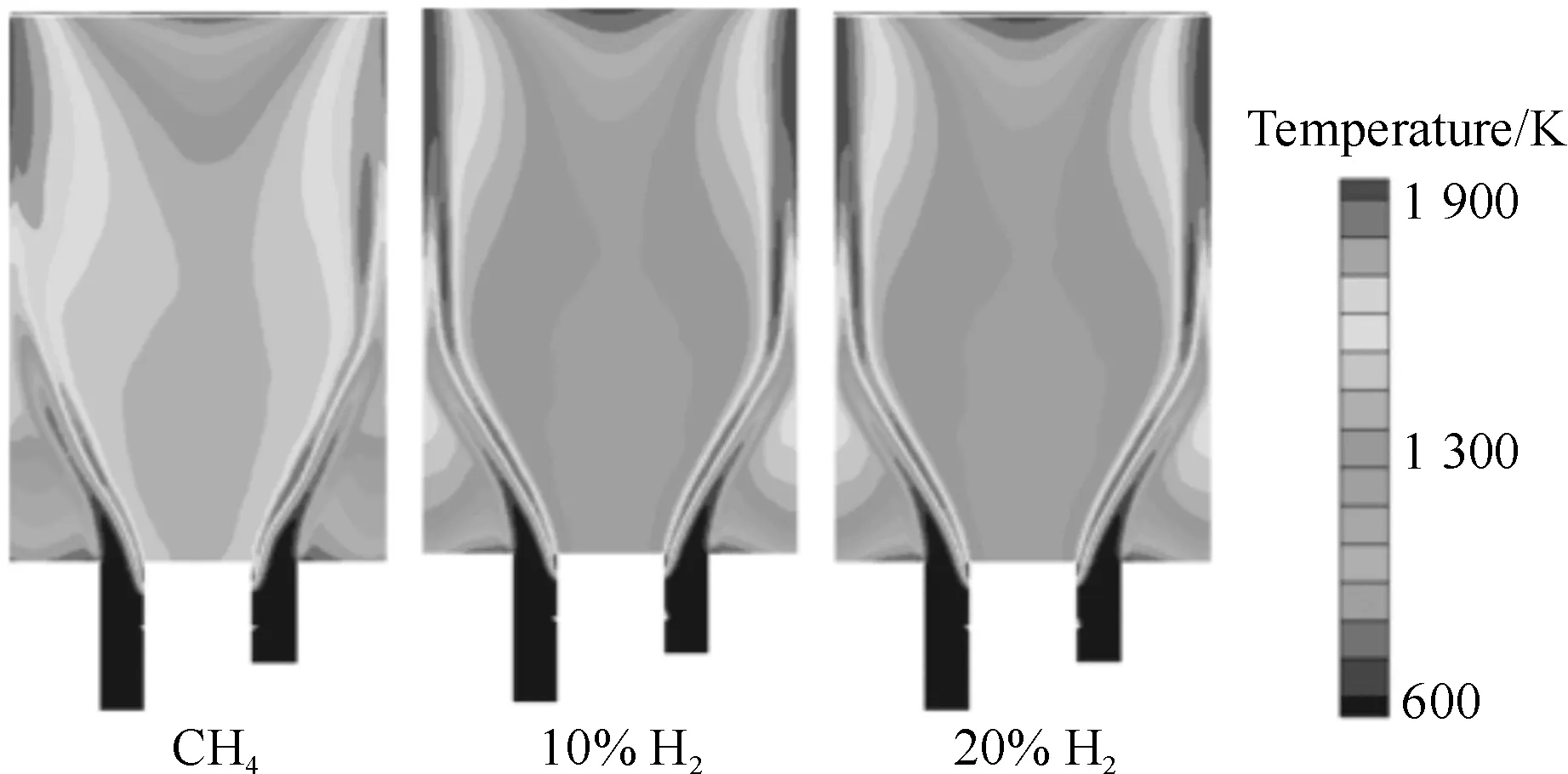
图4 不同氢含量的温度场

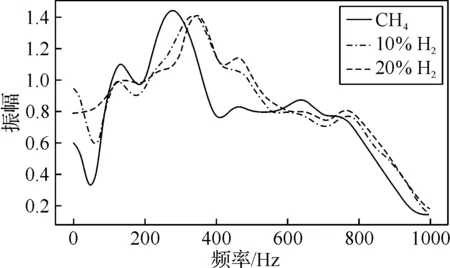
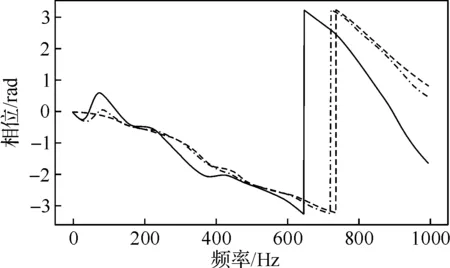
图5 不同氢含量的火焰传递函数振幅和相位

图5所示为三种不同氢气含量下的火焰传递函数振幅和相位。从振幅图上来看，加入氢气后，最大振幅处稍微减小，但就频响的宽度来说，加入氢气明显扩大了不稳定的范围。与甲烷和丙烷的比较类似，加入氢气后，由于氢气的自身特性，燃料的层流火焰速度相比纯甲烷要大，这会增强火焰涡卷，从而使得频响的范围增大。同样的，由于氢气更高的体积热值以及较快的层流火焰速度，使得加入氢气后火焰形态发生转变，扰动传递到火焰前缘的时间相对变短，从而在相位图上看到，加入氢气后的火焰相位差比纯甲烷时要小。

2.2 不同火焰筒限制对动力学的影响

单头部试验台的燃烧室一般来说与工业燃气轮机的截面尺寸和形状有所不同。火焰筒横截面的变化会诱导流场以及火焰的变化。Birbaud等[7]测量了不同火焰筒限制比下的层流火焰传递函数，Hauser等[8]测量了带有径向旋流燃烧器的不同火焰筒限制比下的层流火焰传递函数，均展示了不同限制比下的火焰传递函数差异。本节通过LES计算分析了火焰筒限制对流场、火焰和火焰传递函数的影响。本节采用了两种不同横截面面积的燃烧室进行模拟，一个是84 mm×84 mm的高限制燃烧室，另一个是150 mm×150 mm的低限制燃烧室，针对两种燃烧室采用相同的边界条件。

图6 不同火焰筒限制结构的平均轴向速度场

燃烧室几何的改变会影响燃烧室特征速度，由相关计算可知高限制时火焰筒内特征速度为3.75 m/s，低限制时火焰筒内对应的特征速度为1.176 m/s。特征速度的变化也会对火焰几何及火焰速度产生影响。图6展示了不同火焰筒限制比下中心横截面处的平均轴向速度对比。从图中可以看出，低限制火焰筒内的回流区相比高限制的要更长，同时，低限制燃烧室的回流区要更宽，在越靠近下游的地方，高限制火焰筒的回流区变窄，而低限制燃烧室的回流区则是不断变宽。这与Fu等[9]在绝热条件下研究得出的结论相似。此外，高限制火焰筒在内回流区拥有更大的负速度。回流主要是由旋流诱导的逆轴向压力梯度产生的，会随着不同的当量比产生变化。此外，由于更高的面积膨胀，低限制比的轴向速度在下游区衰减更快。

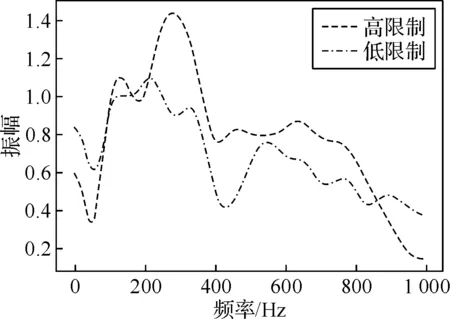
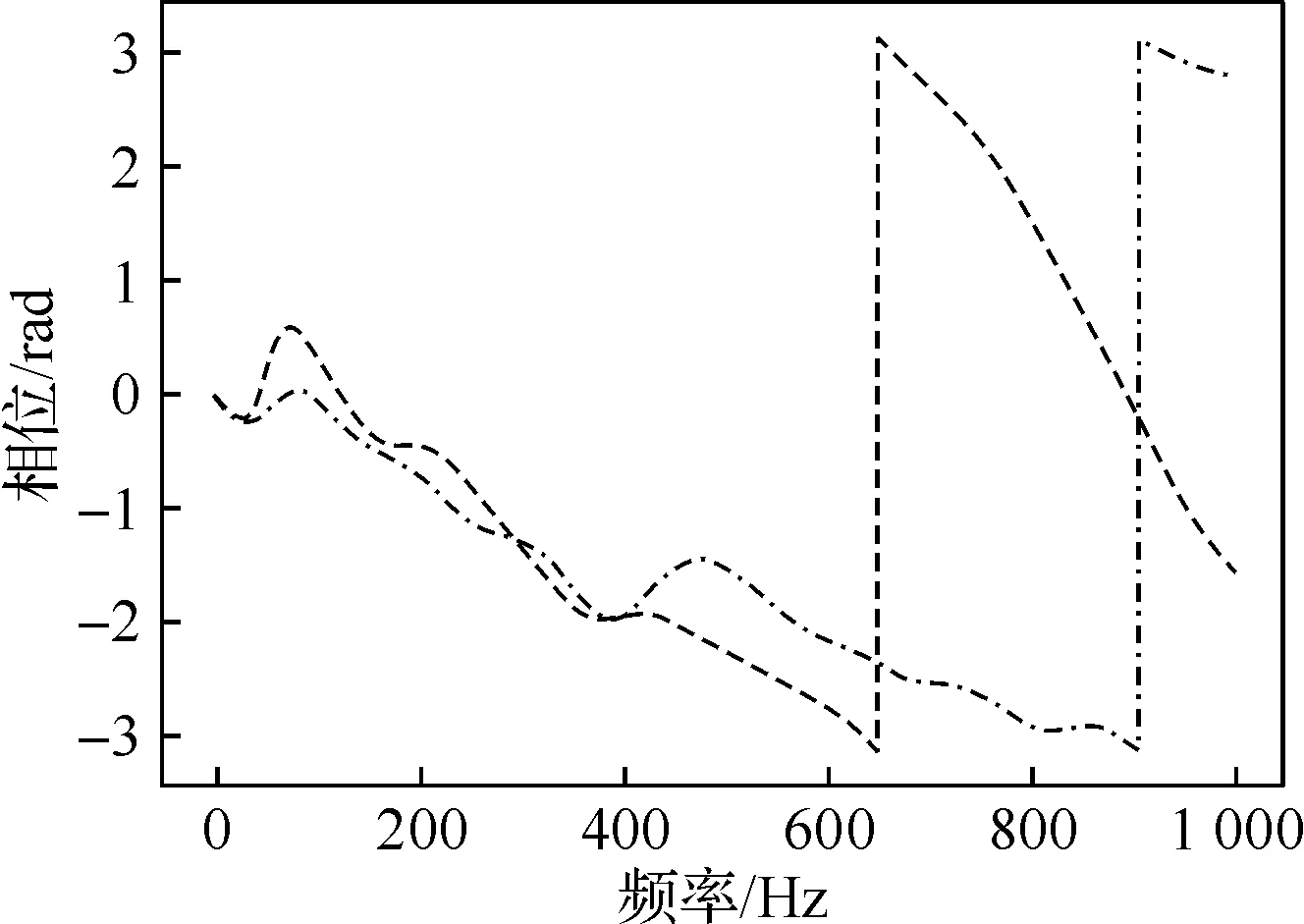
图7 不同火焰筒限制结构的火焰传递函数振幅和相位

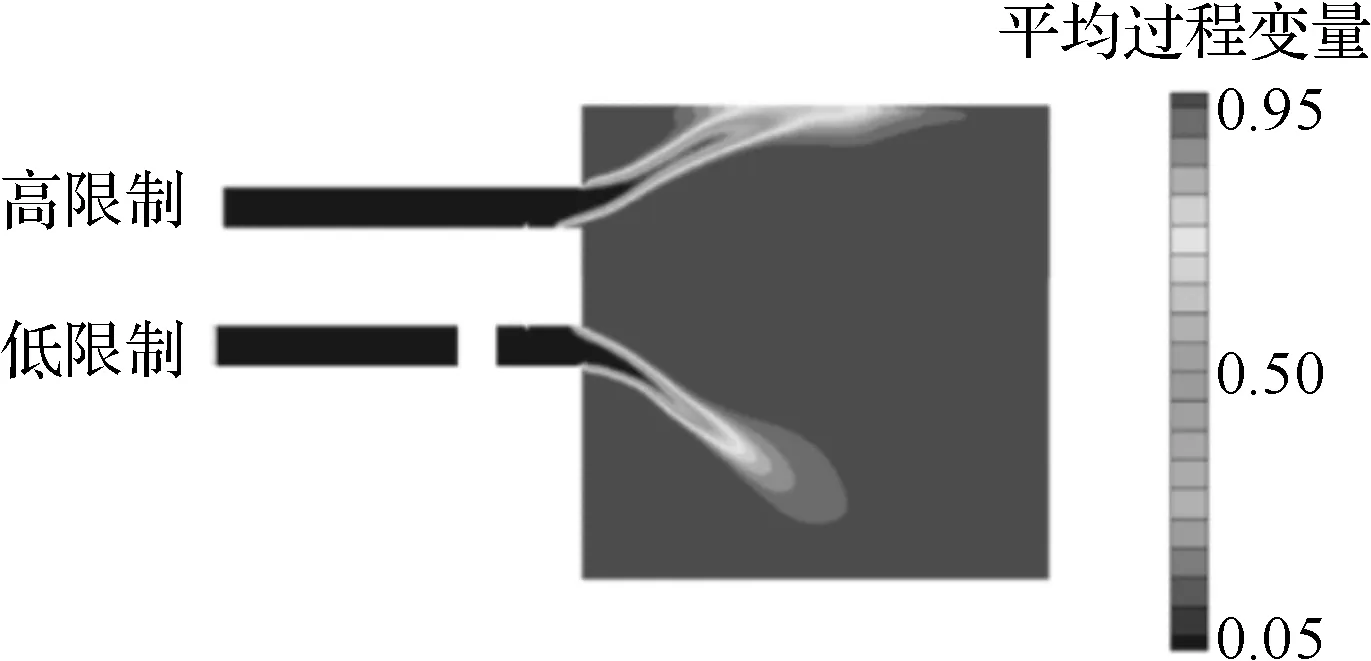
图8 不同火焰筒限制下的平均过程变量

低限制火焰筒的模拟采用的相同的信号激励，激励振幅同样采用5%的平均入口速度。辨识的传递函数与高限制火焰筒的对比如图7所示。对于低限制的情况，其振幅整体走势与高限制有较大差异，如最大振幅相对较低。在约200～350 Hz处，高限制下的振幅大于1，而低限制下的振幅小于1，因此，在此频率段内，火焰更易于捕捉到不同限制比对响应的影响。同时在相位图上可以看到，高限制火焰的相位差相对更大，这是由于高限制情况下火焰与壁面的相互作用较强，因此火焰会沿着壁面拉长，而低限制情况下火焰没有到达壁面，则只拉长到燃料耗尽处，如图8所示。Birbaud等进行的层流情况下不同限制比的实验研究以及Hauser等在径向旋流燃烧器进行的研究中，两种工况下火焰传递函数相位相差较大，高限制比下的相位斜率较大，均与本文相似。

3 稳定性分析

3.1 线性一维声学方程

在声学中，速度(u)、压力(p)和密度(ρ)等流动变量同样可以进行雷诺分解为平均项和脉动项：

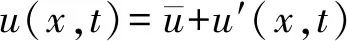
(9)

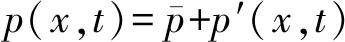
(10)

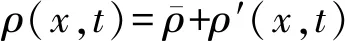
(11)

式中：x和t对应的是位置和时间。脉动项指的是不存在湍流脉动的声学脉动。

考虑到脉动值远小于平均值，因此流动是各向同性的，即流动为等熵的(DS/Dt=0)、均匀的(▽S=0)和非粘性的，且可以通过线性化质量方程和动量方程来获得线性对流声学方程：

(12)

(13)

通过声速a以及压力脉动可以定义密度脉动ρ′：

(14)

将式(14)代入式(12)，同时对式(12)采用全时间导数，对式(13)进行针对x的偏导，两个方程相减以消掉包含声速u′的项，可以得到对流波方程：

(15)

式(15)的解为：

(16)

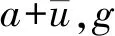
平面谐波随时间变化的形态可以写为：

p′～ei(ωt-kxx)

(17)

则式(15)的解为：

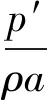
(18)

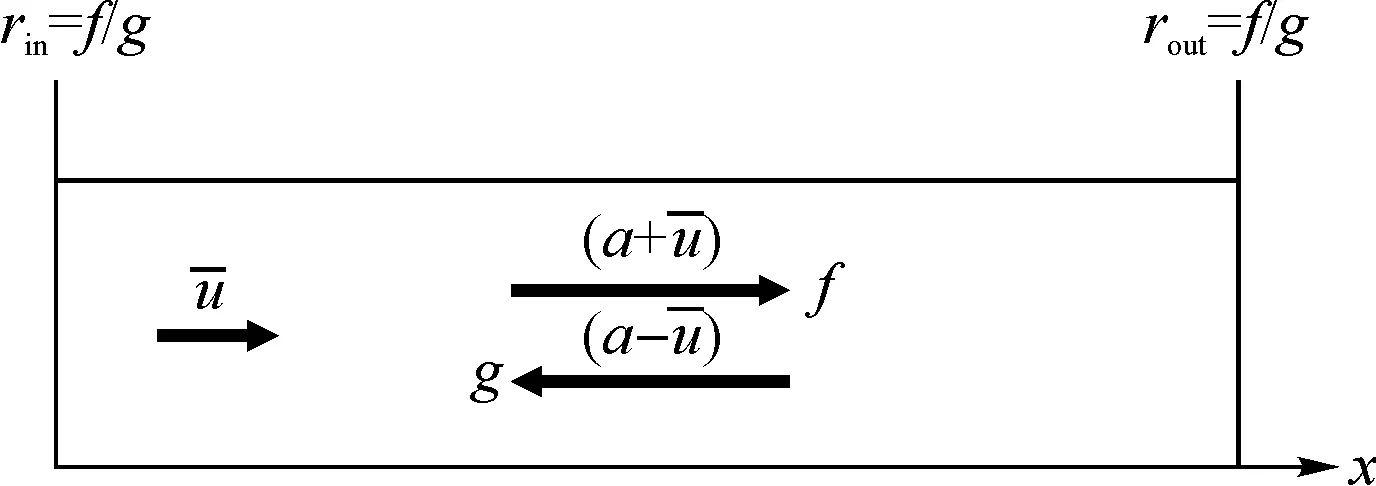
图9 均一流动中的声波传播声波

ω和kx±分别代表角频率和声波数：

ω=2πf

(19)

(20)

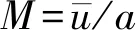
u′=fei(ωt-kx+x)-gei(ωt-kx-x)

(21)

从式(18)和(21)可以看出，黎曼不变量是根据声学脉动p′和u′定义的：

(22)

(23)

3.2 低阶网络模型

低阶网络建模的方法是基于线性以及时间谐和声学的假设，在频域内进行。其核心是整个系统被划分为相互连接的子系统网络，对于研究的燃烧系统来说，就包括了腔室、面积突变、火焰以及火焰筒等，如图10所示。

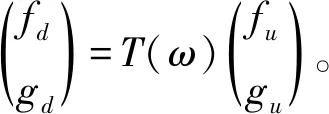
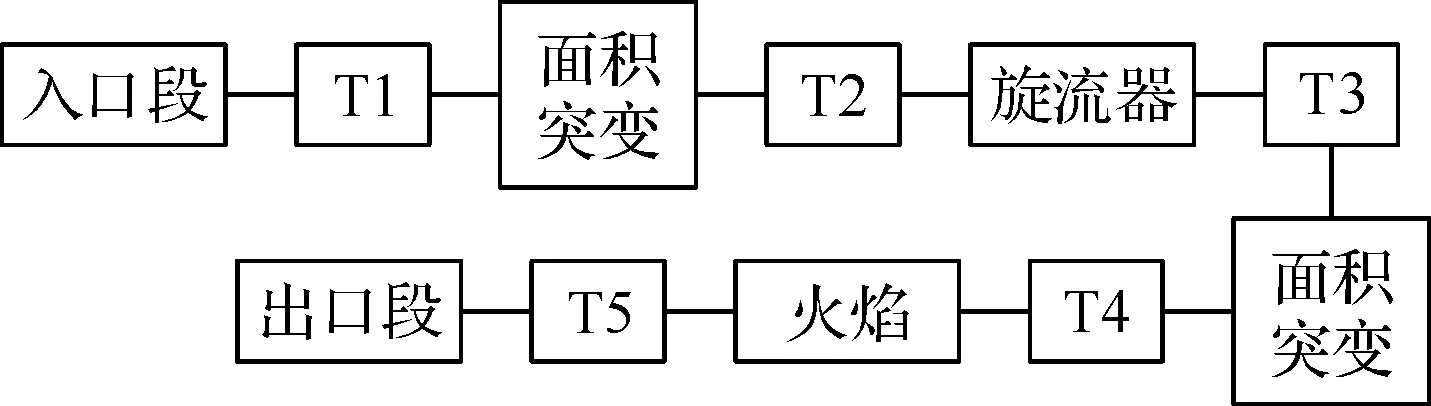
图10 低阶燃烧系统模型

3.3 建模结果分析

本节以15 m/s的入口速度、高限制燃烧室、甲烷为燃料的工况作为参考工况，通过低阶网络建模对其进行的稳定性分析结果如表1所示。可以看出，系统的本征频率为282.5 Hz，同时循环增量大于零，因此系统不稳定。火焰传递函数振幅的增加意味着由一定速度脉动产生的热释放率脉动也在增加。因此，如果满足瑞利准则，作为声源的火焰会向系统施加更多的声能，从而使系统更容易发生热声不稳定。

表1 参考工况的稳定性分析

表2 不同工况下的稳定性分析

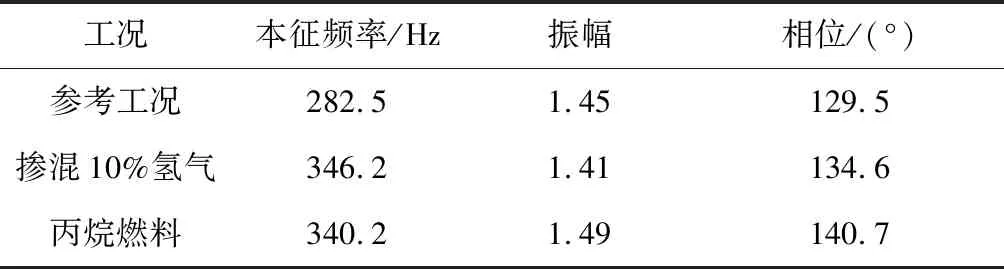
表3 不同工况下的不稳定本征频率对应的火焰传递函数振幅和相位

如前所述，在使用相同的入口条件以及燃烧室长度等的情况下，当在燃料中掺氢以及采用变化的火焰筒横截面积时，对应的火焰传递函数会有所不同。稳定性分析结果如表2所示。燃料为纯甲烷和掺混氢气情况下的稳定性行为相似，但掺混氢气下的不稳定本征频率更高。当火焰筒由高限制变为低限制时，可以看到系统由不稳定转变为稳定。

不同工况下的不稳定本征频率对应的火焰传递函数振幅和相位如表3所示。振幅均大于1且都接近传递函数振幅的最大值。相位在各不同工况下都接近135°。不稳定的行为证明当入口的速度脉动和热释放脉动之间的相位差在135°左右时，同时火焰传递函数振幅大于1，系统会满足瑞利准则。

当火焰筒变为低限制时，135°相位对应的频率为262Hz，其对应的火焰传递函数振幅为0.956。此振幅比高限制燃烧室在本征频率时对应的振幅要小，证明传入到系统的声能要小，系统呈稳定状态。本文没有进行声平衡分析，但是稳定性分析证明了在设计过程中，如果系统出现不稳定本征频率且相位已被识别，可以通过改变火焰筒的宽度来寻找在当前传递函数相位下具备较低振幅的火焰响应。同时稳定性分析也证明燃烧室边界条件对稳定性有重要影响。