让每一次跨越都具有成长的意义——“长方形和正方形面积的计算”教学思考与实践

□ 薛正桧

“长方形和正方形面积的计算”是“图形与几何”领域内一节具有典型意义的“种子课”，教学思路总离不开“猜想—验证—应用”。难道这节种子课只能这样上吗？在品读了老子的《道德经》后，笔者受到了启发，现以“跨越”为主线，设计并实践这一课，教学如下。

一、从“观察”到“操作”的跨越

1.①和②相比，哪一个面积大？你是怎么知道的？

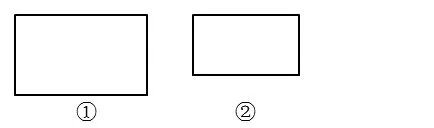
2.③和④相比，哪一个面积大？你能确定吗？

3.有什么好办法能比较出③和④的大小？（摆上相同大小的方格）

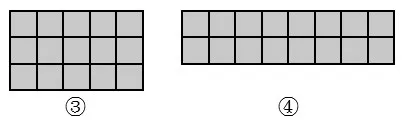
面积作为一种量，是可以直接计量的，它与长度的计量方法一样，都是用相应的单位量（1厘米长的线段、1平方厘米大小的正方形等）与测量对象进行比较，从而得到相应的结果。从本质上看，面积计算其实就是单位面积在数量上的累加。比较两组图形面积的大小，让学生体验到当观察不能起作用时，直接计量才是确定面积大小的基本方法。学生在认识面积单位时，已经会用1平方厘米的正方形直接测量被测平面图形的大小，这是一次承前启后的活动。从观察到操作，是学生对面积大小由定性把握到定量刻画的一次飞跃。

二、从“直接”到“间接”的跨越

1.用边长是1厘米的小正方形计量这些长方形的面积，看谁又对又快。（长和宽都是整厘米数）

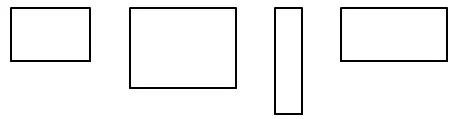
2.小正方形不够了，怎么办？

3.你最少用几个小正方形就能量出它的面积？

这里长方形面积的计算体现了操作由直接计量向间接计量的过渡，这个过程对学生理解其他平面图形的面积计算方法、形成解决有关面积计算问题的一般策略有着十分重要的影响。看谁又对又快，是在速度上提出了要求；小正方形不够了，是借新问题的刺激“逼迫”学生采用比铺满整个长方形更为“经济”的操作。而最少用几个小正方形，是引导学生逐步想到“沿相邻的边框摆”“内部斜摆”等优化做法，即利用“长边和宽边分别能摆几个”来推测“一共能摆几个”。从直接到间接，学生的研究方式有了思维的参与。

三、从“高维”到“低维”的跨越

1.你能根据下图中长度的计量结果，推想出面积的计量情况吗？（每一小段长度1厘米）

2.只计量长度，你能推算出下面这几个长方形的面积吗？

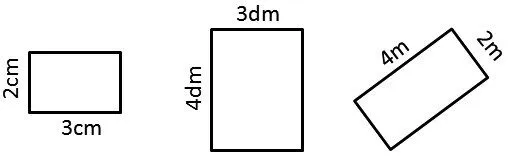
实际解决问题时，人们总是在不断地求简、求优。一维的计量是最原始的，二维、三维的计量虽然可以直接计量，但大家通常都是先计量与被测物相关的一维量，然后再利用一定的规则，通过计算得出结果。由此可见，用公式计算面积其实就是在间接计量的基础上，利用长度来求面积，即计量出长方形的长边、宽边分别能摆几个小正方形，然后相乘。当教师利用推想、计算两个环节把这一演变过程展示出来以后，学生对算理的理解自然就通了。用单位长度（1厘米、1分米、1米等）来量长方形的长和宽，建构面积计算的模型，是学生原有经验的提炼、升华。

四、从“计量”到“计算”的跨越

1.结合下面的图示，说一说如何计算这个长方形的面积。

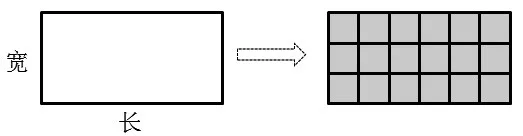
2.长方形的面积怎样计算？为什么？

与单位长度累加不同的是，单位面积累加后要抽象出相应的公式。理解面积计量的原理，是基于学生已有的测量经验、推算经验，引导他们进一步展开深入的思考，确信长方形的面积与它的长、宽存在某种关系，他们完全可以自主推导出公式。长方形的长意味着每排摆几个，宽意味着摆几排，面积则意味着一共摆了多少个，所以长方形的面积＝长×宽。长方形的面积从计量转向了计算，操作活动升华到了思维活动。

五、从“归纳”到“演绎”的跨越

1.你会照样子推导正方形的面积计算公式吗？（可以结合图形来说）

2.你能根据长方形的面积公式推导出正方形的面积公式吗？

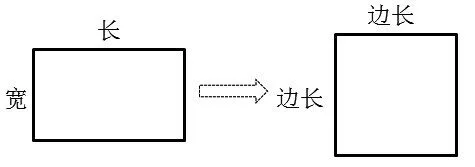
基于儿童的思维习惯擅长于直观的特点，他们往往从一个个相关的实例中找到规律（不完全归纳），进而获得结论，但数学更热衷于用“演绎”（从一般到特殊）获得结论。小学数学学习既要基于儿童，也要发展儿童，从正方形面积公式的推导来看，可以根据长方形与正方形的属种关系进行演绎推理。让学生说一说自己喜欢的方法是对他们思维即时水平的测定，让学生试着用“正方形是长和宽相等的特殊长方形”来推导是对他们思维发展方向的期待。

“长方形和正方形面积的计算”一课中的五大跨越，让学生的数学学习像种子的生长一样充满了生命的意义。