例谈三角形中的最值问题解法途径
2019-10-14江苏省海门中学226100
中学数学研究(江西) 2019年10期
江苏省海门中学 (226100)
杨智慧
例题在ΔABC中,若sinC=2cosAcosB,求μ=cos2A+cos2B的最值.
在三角形背景下的最值问题解法途径:对约束条件的转化,以及对目标函数的变形处理,化归到易处理的目标函数.在三角形下两条路线可寻,一条为选取恰当的变量代数换元,利用导数、均值不等式等进行处理;另一条为保留角元,利用三角恒等变换公式重构约束条件与目标函数,化为三角函数求解最值问题.本文利用四种解法处理一道三角形中的最值问题,以便读者参考.
一、构建代数函数求解

令x=tanA,y=tanB,则x+y=2,x>0,y>0,其中y=2-x>0,所以x∈(0,2).

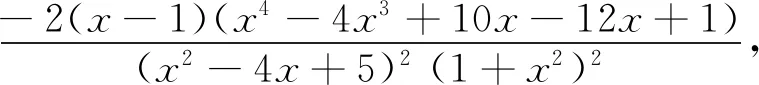
方法二:(平均值换元构建代数函数)令tanA=1-t,tanB=1+t,其中t∈(-1,1),则目标函数
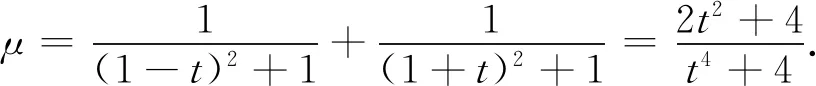

二、保留角元构建三角函数模型
解法四:利用三角恒等变换公式——升降幂公式就、辅助角公式及和差化积公式(积化和差公式)对约束条件及目标函数作合理变形,化归至单名单角的三角函数式.对约束条件sinC=2cosAcosB整合,由cos(A+B)+cos(A-B)=2cosAcosB可化简到cos(A-B)=sinC+cosC,对目标函数μ=cos2A+cos2B=(cosA+cosB)2-2cosAcosB


