巧用向量投影解题 渗透数学核心素养
2019-10-14安徽省合肥市第一中学230601
中学数学研究(江西) 2019年10期
安徽省合肥市第一中学 (230601)
谷留明

学生对投影大多只停留在知道概念的层面,纵观近几年高考和模考题,很多几何方面的最值或范围问题,都可以巧妙地运用投影解决.这个过程,很好地渗透了数学抽象、直观想象、逻辑推理等数学核心素养.
1.投影在向量中的应用
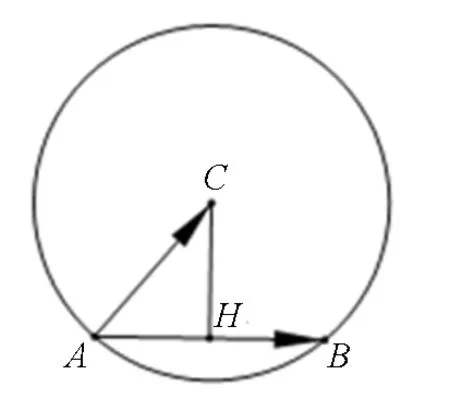
图1
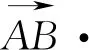


2.投影在解析几何中的应用

图2
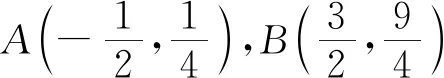


3.投影在解三角形中的应用

分析:根据条件分析出BC⊥AC后,用数量积的定义或坐标法都可以,但巧妙运用投影,更加简洁、直观.

4.投影在立体几何中的应用
例4 (2009年江西高考卷理科第20题)在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心,AC为直径的球面交PD于点M,交PC于点N.(后两问是追加的变式)
(1)求证:平面ABM⊥平面PCD;
(2)求直线CD与平面ACM所成角的大小;

图3
(3)求点N到平面ACM的距离;
(4)求点N到直线AM的距离;
(5)求直线BP到直线AM的距离.
分析:对于后三问,若用传统几何法,则每一问都要独立分析,需要很强的空间想象能力.而用投影,有较为统一的解题模式,整体上比较高效,能提高学生的数学抽象、直观想象与数学运算的素养.
解:(1)、(2)略.
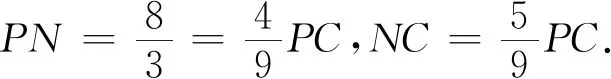



5.投影在线性规划中的应用

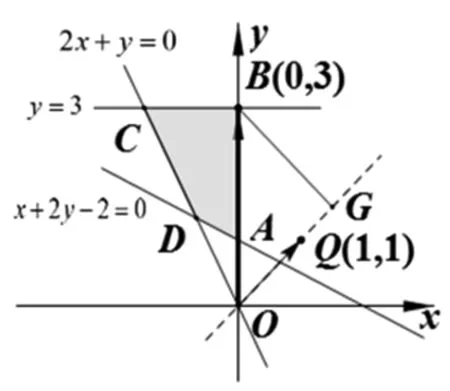
图4
分析:用线性规划的方法,当然可以.但从目标函数的结构,可联想到坐标形式的数量积,再用投影来解决,这是一种巧妙的方式,渗透着数学抽象、直观想象的核心素养.
由上可知,很多司空见惯的题目可以用投影巧妙地解决,并渗透着多种数学核心素养.因此平时的教学中,应回归定义,吃透概念的内涵与外延,并与其他章节的知识有机整合,已达到“随风潜入夜,润物细无声”的境界.
