巧用配方法妙解一类向量最值问题
2019-10-14新疆生产建设兵团第二中学830002新疆乌鲁木齐市第八中学830002
中学数学研究(江西) 2019年10期
新疆生产建设兵团第二中学 (830002) 新疆乌鲁木齐市第八中学 (830002)
张国治 蒲星瑞 王盈茜 王妍喆
向量知识在新课程中有着举足轻重的作用,蕴含丰富的内涵,笔者近期研究发现,有一类涉及最值的向量问题可以通过“减元”的策略利用配方法和沙尔定理快速获解,极具可操作性,可推广.
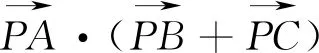

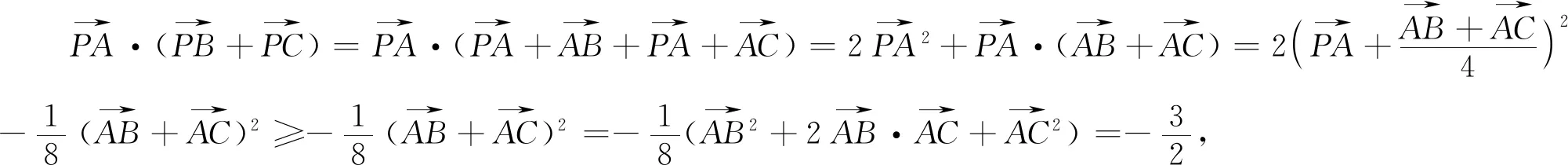
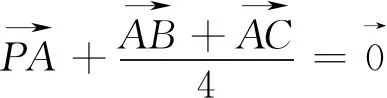



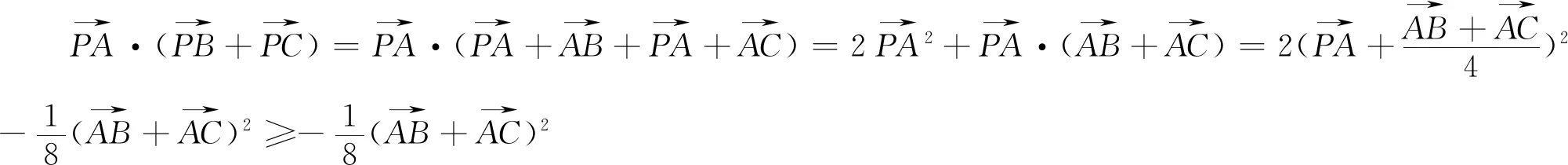

评注:显然例2是在例1的基础上改编而来.按上述解答不难将例1、例2做如下更一般的推广.
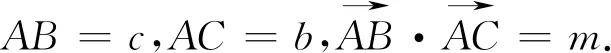
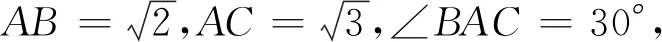


评注:按上述解法不难做如下推广.
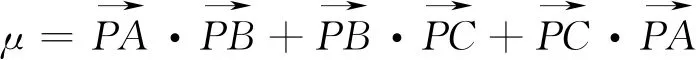
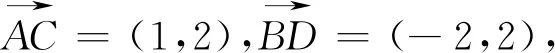
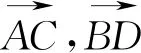

评注:按上述解答可将例4做更一般的推广.



A.内心B.外心C.重心D.垂心

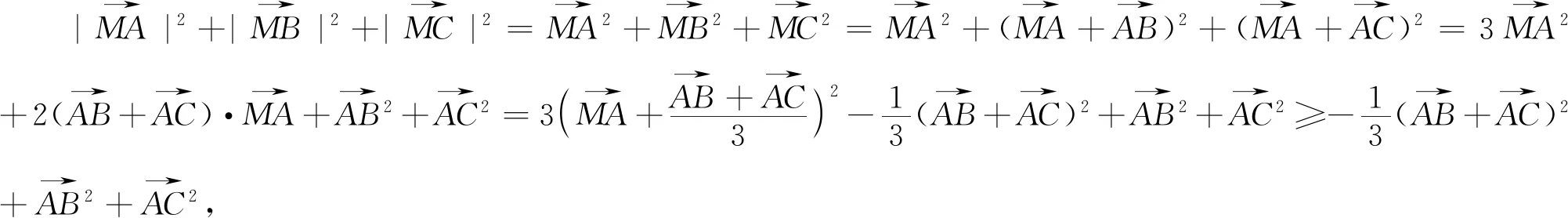
评注:到三角形三个顶点距离之和最小的是费马点,而重心到三角形三个顶点距离平法之和最小.
配方法若用到向最值问题的求解中,充分挖掘题目中的隐含条件,以“减元”的思路基本策略,辅以沙尔定理使得一类向量最值问题能高效获解.解决一个比较复杂的问题,‘退’到最简单最原始的解题思路,把这个最简单最原始的问题想通了想透了”然后再进行归纳、综合而实现质的飞跃,“这是学好数学的一个诀窍”.
