简约而不简单
——多视角探求一道二元函数最值题
2019-10-14江苏省通州高级中学226300
江苏省通州高级中学 (226300)
严振君
一、题目呈现

乍看本题,给人以条件简单,目标清晰之感.教学中,经过与学生共同探究,感觉此题实则“简约而不简单”,可从多个视角切入,用不同方法探求,是一道颇具韵味的“好题”.现将本题的解法作一个梳理,与读者交流分享.
二、解法荟萃
视角一 等式减元 导数求解

评注:“减元”是求多元函数最值问题的常规处理策略.由于x,y均为正数,则可将条件中的等量关系化隐性为显性,将二元目标函数转化为一元函数.此法涉及到复合函数求导,对运算要求较高,但思路清晰,目标明确,易于接受.
视角二 三角换元 意在简化

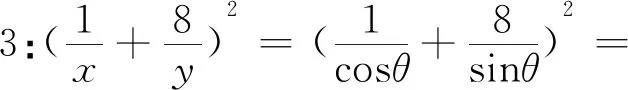

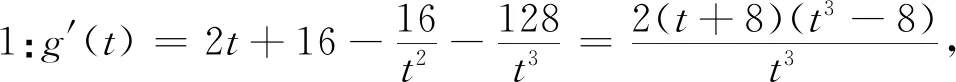


视角三 “1”的代换 整体换元
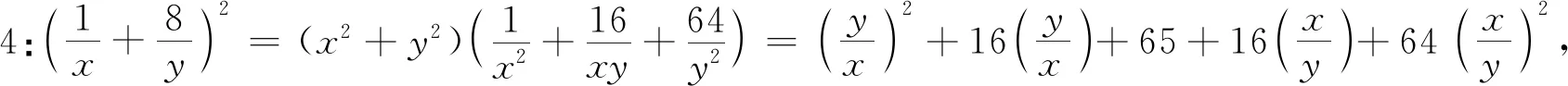


视角四 引入新元 变量归一

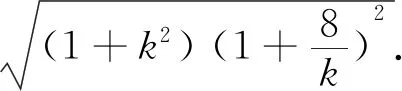
评注:此法也称作“倍值换元”,即通过引入新元k,沟通旧元x和y的直接联系.结合条件等式,将原先变量x与y均化归为新元k,将二元目标函数一元化.
视角五 方程思想 彰显通法
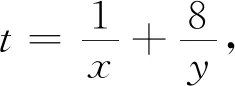

视角六 数列向量 另辟蹊径


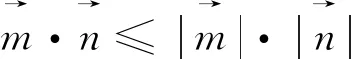
视角七 数形结合 形象直观

图1
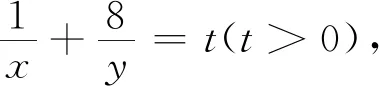
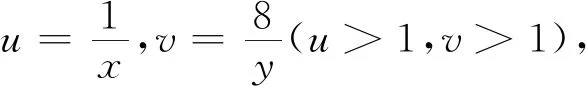
评注:“数形结合”的思想启示我们要善于挖掘代数问题背后的几何特征.“以形助数”可以让问题的解决更为直观简捷,但又不失严谨.方法11从变换的视角,将目标函数线性化,原题得以“改头换面”,借助于线性规划的方法求解.
视角八 高数观点 高屋建瓴


评注:拉格朗日乘数法是高等数学中求多元函数最值的常用方法.尽管使用拉格朗日乘数法的条件较为苛刻,但操作并不复杂,学生易于接受,对于约束条件下求最值问题可以尝试.
视角九 待定系数 巧妙配凑

评注:观察本题的条件和目标,符合使用三元均值不等式的结构特征.用待定系数法可以突破“配凑”系数的难点,方便直接.
视角十 不等式法 自然天成
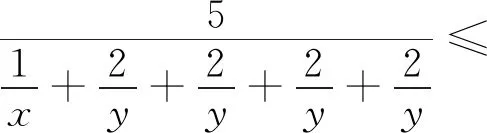
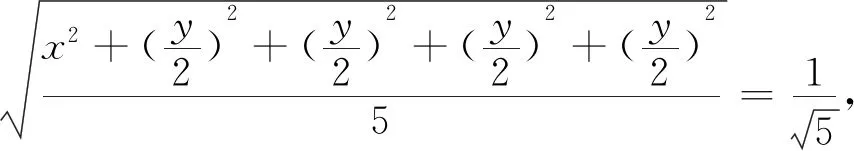


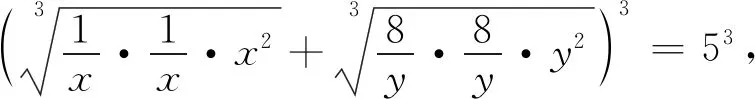

三、拓展延伸
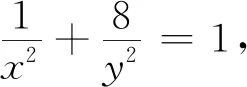

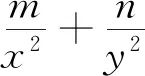
限于篇幅,请读者自行尝试证明.
四、解后反思
在解题教学中,要引导学生善于从不同的视角审视题意,启发学生灵活地从问题的不同侧面、不同层次进行全方位的探讨,拓宽学生视野,发散学生思维.在一题多解的基础上,还需引导学生对多种解法进行对比分析,择优而从,达到弄透一题、旁通一类,举一反三、事半功倍的良好学习效果.善于从不同视角思考和解决问题,除了帮助学生完善知识结构外,还能起到活化思维,激发兴趣之功效.
