巧用基本不等式 妙解最值问题*
2019-10-14广东省惠州市东江高级中学516000湖北省黄冈市长冲高级中学438700
广东省惠州市东江高级中学 (516000) 湖北省黄冈市长冲高级中学 (438700)
李 旭 唐松明
基本不等式是高中数学教学的重要内容,也是高考的热点问题,但在高考命题中,很少能够见到直接考查基本不等式的题目,往往是将基本不等式与三角函数、解析几何、恒成立问题、数列、向量等问题结合起来.在历年的考试题目中,这类结合问题大部分是以最值问题展现出来,而最值问题的求解技巧灵活,学生在学习过程中普遍感觉困难,往往不知何时运用基本不等式,以及该用基本不等式中哪个公式.本文将对上述问题结合今年的模考题和往年的高考题加以说明,解析处理这些问题的通解通法,与各位师生共享.
一、基本不等式回顾及运用
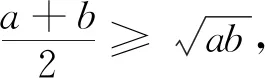
利用上述的基本不等式,易得如下的几个重要不等式:
(1)a2+b2≥2ab(a,b∈R).
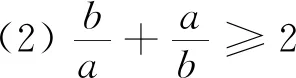
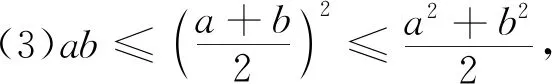
在高中数学教学中,上述五个不等式是教学的重点内容,需要学生熟练掌握并能合理运用解决相关题目,我们首先来看如下的例题:
例1 已知a>0,b>0,ab=a+b+3,求a+b的最小值.
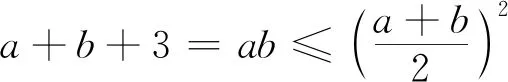
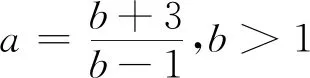
变式1 已知a>0,b>0,ab=a+b+3,求ab的最小值;
变式2 已知a>0,b>0,ab=ka+b+3,其中为k正数,求ab的最小值;
变式3 已知a>0,b>0,kab=la+b+3,其中为k,l正数,求ab的最小值.
从例题和变式问题的解答过程中我们可以得出以下两个简单的结论:
已知x>0,y>0,则
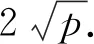
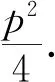
二、基本不等式运用再探究
第一节中,结合基本不等式我们讨论了与之有关的最值问题的一般解法,显然上述例题是基本的,而高考的命题原则是来自课本但要高于课本.为此,我们结合最近的高考模拟题进一步讨论基本不等式在最值问题中的运用.
1.与三角形问题相关联
例1 (2018江苏高考理科卷第13题)在ΔABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为.
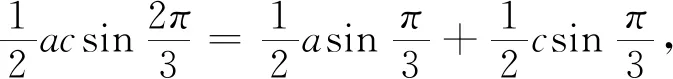
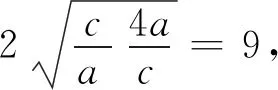
评析:先根据三角形面积公式给出等式条件,再利用基本不等式求问题的最值.在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧以及基本不等式成立的条件:一正二定三相等,其中“正”表示字母为正数;“定”表示不等式的另一边必须为定值;“等”即等号取得的条件.只有满足上述条件才能应用基本不等式,否则会出现错误.
2.与解析几何问题相关联
例2 (武汉市2019届高中二月份调研数学卷(理))已知A,B为抛物线y2=4x上两点,O为坐标原点,且OA⊥OB,则|AB|的最小值为( ).
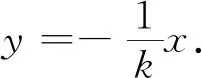
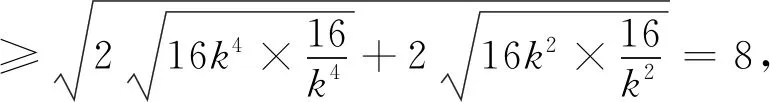
评析:本题主要考查直线与抛物线的位置关系以及利用基本不等式求两点间距离的最值问题,对于这样一道选择题,需要学生对公式的记忆和运用都要十分熟练.同时,如果把本题中的抛物线换成椭圆或双曲线我们又该如何得到什么样的结果呢?希望读者可以做更进一步的探讨.
3.与恒成立问题相关联
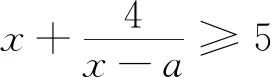
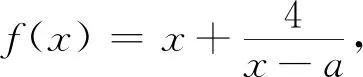
评析:本题看似简单,但实际上蕴含了很多重要的数学思想.当然,如果题设中的a换成关于a函数g(a),这时就需要再一次处理g(a)+4≥5恒成立问题.类似的变化还有很多,但这些变化都是形式上的,本质依然是处理不等式最值问题的方法技巧.
4.与数列问题相关联
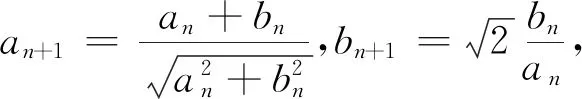

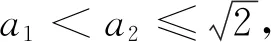
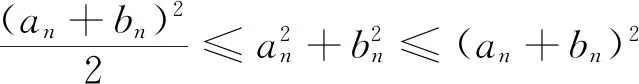
5.与向量问题相关联
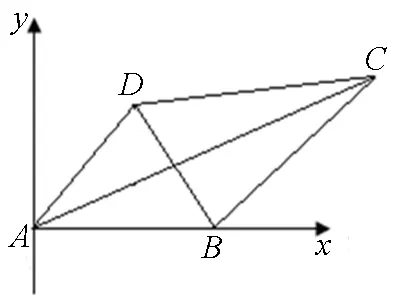
图1
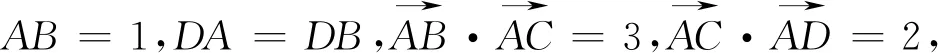
解析:如图1所示,以A点为原点,建立平面直角坐标系,其中A(0,0),B(1,0).
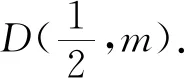
评析:本题考查了向量中模长的相关知识,在利用向量数量积的几何意义的同时涉及到不等式的放缩问题,如何巧妙且恰到好处的运用基本不等式是关键.合理建立坐标系,巧妙设点,数形结合,几何问题代数化是解决本题的主要思路.
三、反思感悟
考题千变万化,但万变不离其宗.教师在教学中一定要把握基本不等式的核心——“一正,二定,三相等”:一正是首先要判断参数是否为正;二定是要看和或积是否为定值(和定积最大,积定和最小);三相等是验证等号能否成立(主要注意两点,一是相等时参数是否在定义域内,二是多次用“≥”或“≤”时等号能否同时成立).
同时,我们希望教师自己能合理选取例题,掌握命题技巧,洞悉事物间的本质联系,希望我们的学生能通过对有限典型例题的学习,去领悟到那种解无限道题的数学机智;我们教学的对象不是题目,而是鲜活的个体,是持续发展中的学生,所以教学内容需要丰富,课堂呈现必须生动;我们教育的目的不仅是会做题,更是要培养学生学会发现、学会思考,用知识解决问题、用理性欣赏世界!
