一道教师解题技能竞赛题的命题手法探究

江西省南昌市第十五中学 (330039)

龙光鹏

1.试题呈现

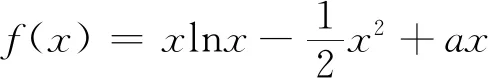
(Ⅰ)求实数a的取值范围；

这是2019年3月1日南昌市高中数学教师解题技能竞赛的21题，试题设计新颖，内容丰富，具有一定的难度.如能探明试题的本源，必将有助于理清试题的解题思路，那么命题者是如何命制出这道试题的呢？带着这个疑问，笔者展开了命题本源的探索之旅.

2.执果寻因

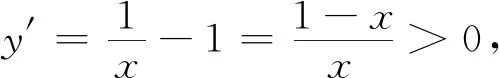
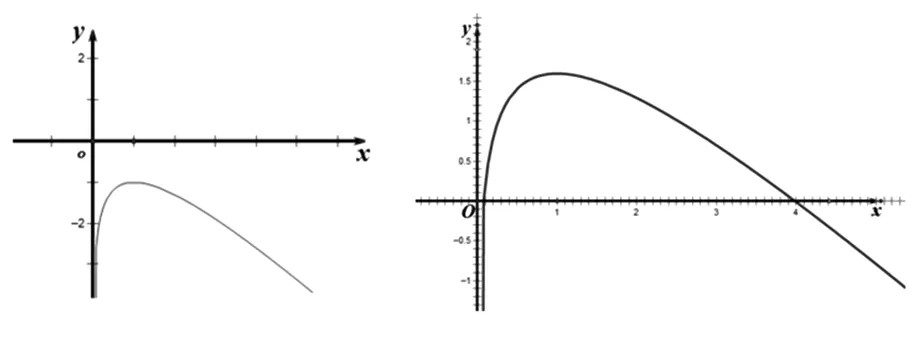
图1 图2

得知函数y=lnx-x无零点，于是将函数y=lnx-x图像向上平移a(a>1)个单位长度得到函数y=lnx-x+a，其图像如图2所示.

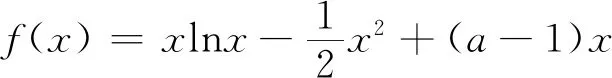
第(Ⅰ)问设计为：求实数a的取值范围；是高考常规考查的情形，为大家所熟悉.

然而在(Ⅱ)问的设置上是怎样在继承中有创新呢？让我们一起来揭开其神秘的面纱！

首先，通过图2发现x1+x2>2，证明如下：

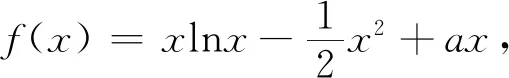
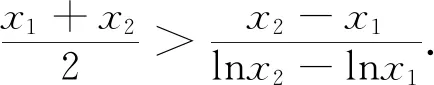
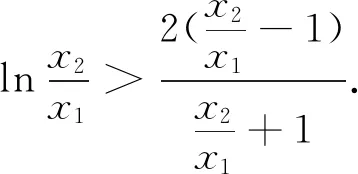
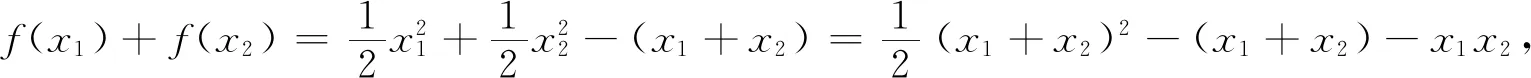
3.命题手法探究

经过探究，笔者发现本题的命题思路是：基于函数极值点、函数拐点、类比对称中心，结合切线放缩.其主要还是考查拐点偏移问题.

我们知道，若函数f(x)关于点(a,b)成中心对称，则有f(x)+f(2a-x)=2b.迁移应用此对称的思想，我们得到：若函数f(x)有拐点(a,b)，则可以探究位于拐点两侧具有一定对称特征的两点与拐点的关系.如若函数f(x)有拐点(a,b)且x1+x2=2a，则试探究f(x1)+f(x2)与2b的关系.

4.命制新题

模仿上述的命题手法，笔者命制如下试题：

已知函数f(x)=(x+1)lnx-ax有两个极值点x1,x2.

(Ⅰ)求a的取值范围；

(Ⅱ)求证：f(x1)+f(x2)<2a-8.

解析：(Ⅰ)易得a>2；