Nesbitt不等式的精彩演绎
2019-10-14福建省仙游第一中学351200
中学数学研究(江西) 2019年10期
福建省仙游第一中学 (351200)
林碧霞
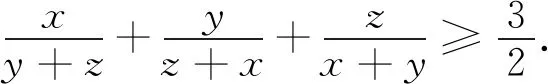
这个不等式形式优美,内涵极其丰富,由此可以演绎出一系列的不等式,可谓花团锦簇、精彩纷呈.
一、由Nesbitt不等式直接演绎


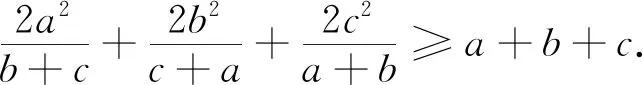
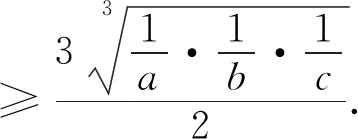
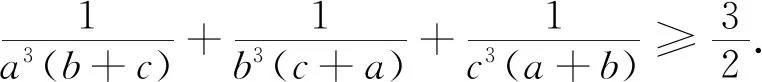
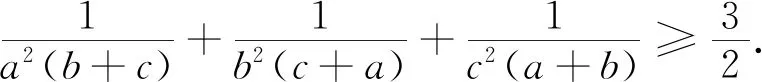


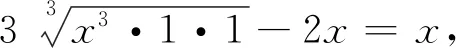
这就得到并证明了2006年白俄罗斯数学竞赛试题.

二、演绎Nesbitt不等式的变式


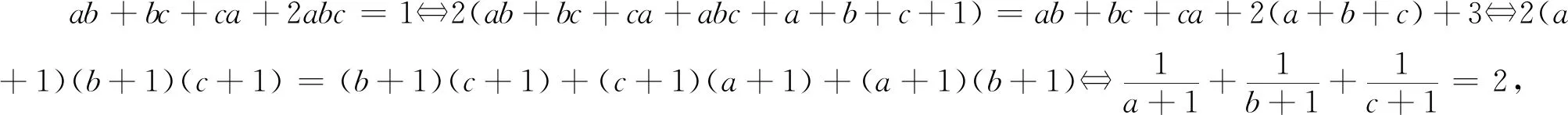
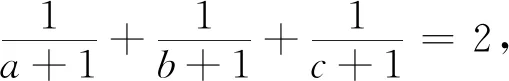
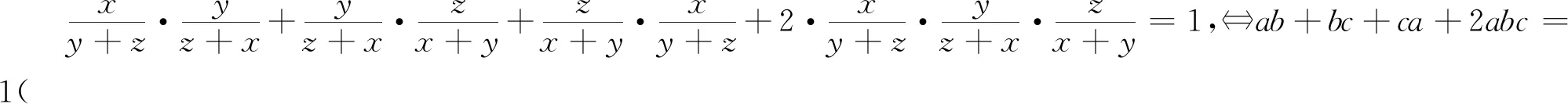
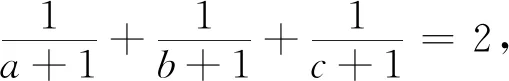

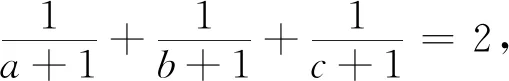
三、由Nesbitt不等式的变式再演绎



例8 已知x,y,z是正数,且xy+yz+zx+2xyz=1,证明:2(x+y+z)+1≥32xyz.
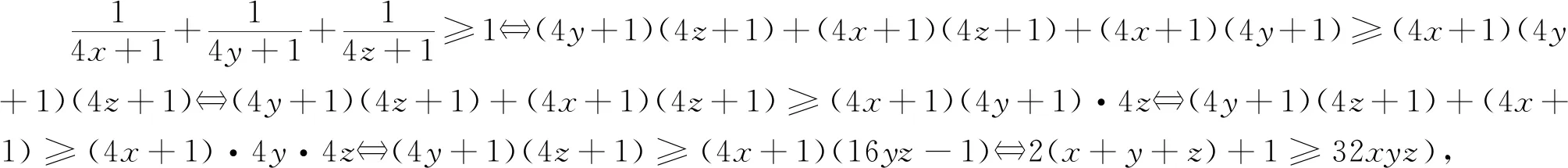
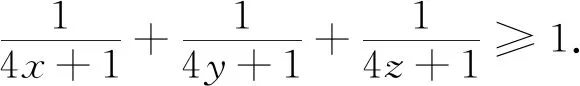
例10 已知x,y,z>0,且xyz+xy+yz+zx=4,求证:x+y+z≥3.



例13 设x,y,z>0,且xy+yz+zx+xyz=4,求证x+y+z≥xy+yz+zx.
例14 已知a,b,c>0,且abc=a+b+c+2,求证:ab+bc+ca≥2(a+b+c).

