《数学通报》第2414号问题的推广
2019-10-14贵州省都匀一中558000
中学数学研究(江西) 2019年10期
贵州省都匀一中 (558000)
夏开平

这是《数学通报》2018年第4期数学问题解答栏目中刊载的2414号问题,它形式优美,内涵丰富.细读安老师利用构造三次函数结合导数知识给出的证明,受益匪浅.深入探究发现,该问题可以做如下推广:

证明:由已知a,b,c>0,a+b+c=3,λ≥1.
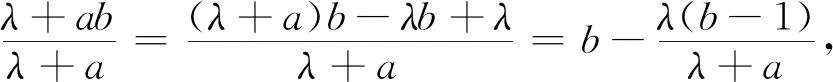
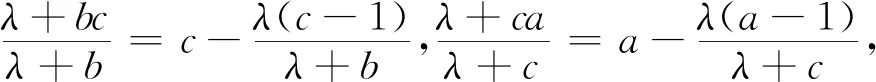
由简单不等式3(ab+bc+ca)≤(a+b+c)2=32=9,得ab+bc+ca≤3.由(a-1)2b+(b-1)2c+(c-1)2a≥0展开并移项整理得a2b+b2c+c2a≥2(ab+bc+ca)-3.所以λ(a2+b2+c2)+(a2b+b2c+c2a)+(λ-1)(ab+bc+ca)-6λ≥λ(a2+b2+c2)+[2(ab+bc+ca)-3]+(λ-1)(ab+bc+ca)-6λ=λ(a+b+c)2+(1-λ)(ab+bc+ca)-3-6λ=9λ+(1-λ)(ab+bc+ca)-3-6λ=(1-λ)(ab+bc+ca)-3(1-λ)=(1-λ)(ab+bc+ca-3)≥0.所以(3)成立,(2)获证.
在不等式(2)中,取λ=1即可得《数学通报》数学问题2414.
