“一图多题”的解法及变式赏析
2019-10-14江苏省海安市实验中学226600
中学数学研究(江西) 2019年10期
江苏省海安市实验中学 (226600)
潘新峰
一、题目呈现与分析

分析:题目虽然简短,但是信息量不少:斜ΔABC、重心、AG⊥BG、三角等式.题目是以图形为背景的三角函数题,数学知识方面主要考查三角恒等变形和三角形中边角关系的运算,三角形中正、余弦定理及其相关运算等;数学思想方面主要考查转化与化归,数形结合等思想.综合考查考生逻辑思维、转化、推理及运算等方面的能力.
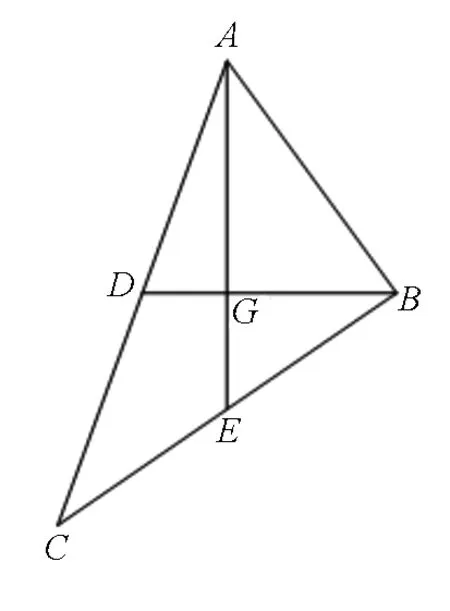
图1
本题是填空题的压轴题,需要考生在较短的时间内完成,考生必须迅速找到解题切入口,理清思路,逐步推进,做出答案.试题的解题方法不单一,为考生的解答提供广阔的想象空间,试题的设置使得考生不仅需要了解高中多章节的数学知识,而且要求考生会利用化归与转化等思想,寻找合理的解题策略,对学生的推理论证能力有较高的要求.本题区分度高,作为高三数学试卷填空题的压轴题,是一道能突出选拔功能的好题.
二、解法赏析
视角1:设边算角
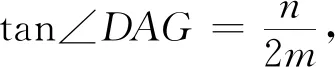
评注:在直角三角形中利用对边比邻边求出小角的正切,进而利用正切的和角公式求出tanA、tanB、tan(A+B)=-tanC,最后求出实数λ的值.
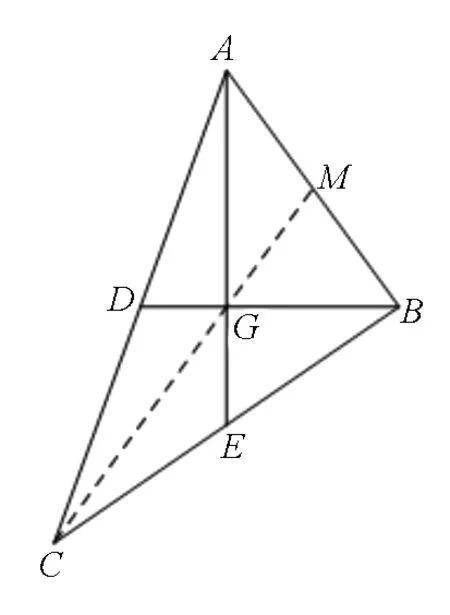
图2
视角2:算边算角

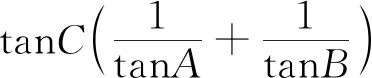
三、变式赏析
变题1 已知点G是斜ΔABC的重心,且AG⊥BG,则sinC的最大值为.
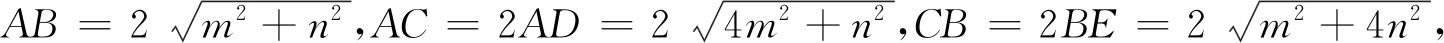
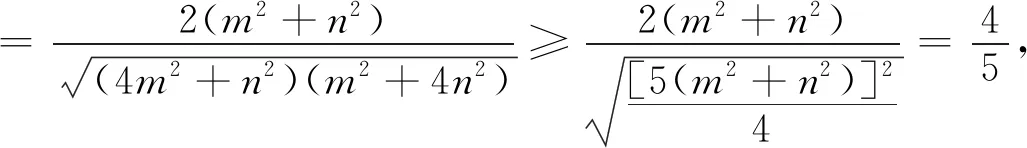
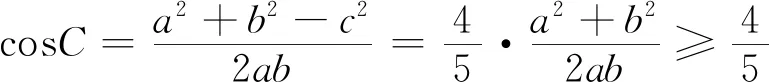
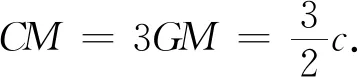


三、结语
“一图多题”中从不同的视角思考问题,这充分体现高考数学题的一道试题往往考查多种能力、多种数学思想;同时,高考题在命制时充分考虑考生数学能力的差异,不少试题的解答方法不是唯一,在平时的训练中,利用一题多解,给学生提供较大的思维空间;在平时的选题时,题目要贴切教学实际,重视数学的基本能力与思想方法训练,所以,我们在平时的学习和训练中重视知识的储备和方法的积累,才有可能迅速切入,找到解题的突破口,达到事半功倍的效果.
