立足数学素养培育,探析导数试题命制*

福建省石狮市华侨中学 (362700)

蔡振树

命题是艰辛而又富有挑战性的工作，积极参与命题活动，可以加深对数学知识本质方法的理解，加深对高考考试说明的要求等方面的领悟，强化知识与方法体系的建构，提高教师自身业务素养，提升课堂教学的有效性.试题命制中关于数学核心素养的考查如何落实到位，六大数学核心素养如何在解题过程中考查落地，是命题者需要重点研究的课题.下面笔者以函数导数试题的命制过程评析为例，结合多年参加各级考试命题的经历谈几点感想.

一、立足基础知识的考查，培育学习潜能

例1 已知函数f(x)=ax-lnx-1,(a∈R).

(Ⅰ)∀x∈(0,+∞)，bx-2≤f(x)，若f(x)的一个极值点是x=1，求实数b的取值范围；

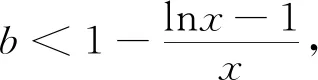
试题(Ⅱ)问是本题的核心，通过设置对参数的讨论，利用导数研究函数的性质，并利用单调性比较大小，考查了分类讨论、推理计算能力.题中函数与不等式结合为学生解答提供广阔的发挥空间，利用导数研究函数的性质要求学生具备一般到特殊的问题转化能力，重点考查学生的数学抽象、逻辑推理等数学素养.

试题评析：导数的应用是高中数学学习的重要内容之一.本试题考查函数的导数及其应用，分步设问，逐步推进，考查由浅入深，重点突出，提高思维层次，使学生更深刻的理解导数的应用，同时对学生的逻辑推理、数学运算等素养落实提供了载体.本题利用导数研究函数的手法，层次分明，区分度高.它比较能反映学生是否真正掌握数学知识本质，使不同层次的学生的思维得到充分展示，进一步考查学生学习的潜能.

二、立足能力思想的渗透，培育学习能力

(Ⅰ)求实数b的取值范围；

(Ⅱ)证明：x1+x2>2.

命制过程:试题源于某模拟考试题，题目如下：

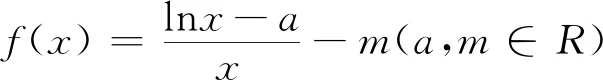
(Ⅰ)求实数m的取值范围；

(Ⅱ)记函数f(x)的两个零点分别为x1,x1.证明：x1x1>e2.

若令t=lnx，则方程可化为t-met=0.

为了提升试题难度，考虑增加考点知识，考查函数的极值，从而修改了题目的条件，得到如下试题：

函数f(x)=x+bex(b为常数)有两个零点x1,x2.

(Ⅰ)求实数b的取值范围；

(Ⅱ)证明：x1+x2>2.

试题评析：本题重点在于对逻辑推理、数学运算等数学素养的渗透，借助函数问题的研究考查本质的数学思想和方法.换元法是编拟试题的一种常用方法，在数学命题中通过换元，可以改变试题的“包装”条件、结论的表述形式、提升或降低试题难度等.在本题的命制过程中，采用换元的方法，将一道含对数函数的问题改编为含指数函数的问题，得到一道“焕然一新”的试题，具有明确考查目标，能根据考查意图合理调整条件与设问，从而使试题自然不造作.本题表述简洁，解法多样，有内涵，考查面广，渗透考查逻辑推理、运算求解等数学核心素养，是能力思想的重要体现.

三、立足数学素养的提升，培育创新能力

例3 已知函数f(x)=lnx-kx+k.

(Ⅰ)若f(x)≥0有唯一解，求k值；

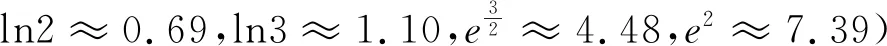
命制过程：着眼数学素养的提升，欲命制一道函数不等式问题作为理科压轴试题，故设想函数背景适当复杂，可含有指数函数、对数函数及幂函数等形式，基于上述想法，本题从(Ⅱ)问的设置开始.

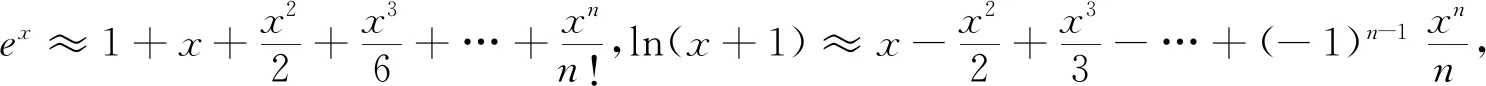
设想三：适当增加解题的难度，引入参数a，当a≤1时，证明不等式ex-xlnx>ax2+1，接下来的问题就是，高中现阶段，学生能否利用所学知识进行证明，证明过程中是否会出现高中现阶段无法解决的情况、难度过大或难度不够等问题，于是命题者模拟学生进行解答.

图1 图2 图3

设想五：(Ⅱ)问的不等式证明，若用到不等式lnx≤x-1进行放缩，则可简化证明过程，故命题者想在(Ⅰ)问中设置与该不等式相关问题，为问题(Ⅱ)做铺垫.构造函数f(x)=lnx-kx+1，讨论f(x)的单调性，或f(x)=lnx-kx+k，f(x)≥0有唯一解，求k值.这两种问法都可以考查到分类讨论思想，而第二种问法可以让学生更好的分析f(x)=lnx-kx+k的图像及直接得出结论lnx≤x-1，至此确定(Ⅰ)问.

试题评析：本题关注学生学习差异，突出创新，探索数学核心素养考查的落地实践，试题分步设问，(Ⅰ)问中的函数f(x)=lnx-kx+k是学生较为熟悉的，从而降低了对学生心理冲击，进而提高试题的效度.通过题目的设问，充分考查多种数学思想，通过对“唯一性”的研究，考查思维的严密性，实现了知识与能力的双重检测.而(Ⅱ)问则将函数与不等式有机结合，对计算难度，思维深度的要求逐步提高，层次分明，差异创新，能较好的达到设计预想.试题对学生的数学素养提出较高要求，无论是推理还是运算，区分度高，让学生思维广度和深度都得到充分发展.

在试题命制过程中，如何探索数学核心素养从理念到实践的落地，问题是载体，构思是关键，引导是路径，提升是目标.函数导数试题属于综合性较强的问题，对其进行合理化设计，可以发挥重要的作用.多种数学核心素养是交叉互相渗透，不能绝对化割裂开来，素养是综合的体现，通过对试题的学习探究是提升学生数学学习能力和核心素养的主要途径.因此通过试题命制过程的研究不仅对教师，而且对学生来说都是有意义的，也是很有价值的.