量子等离子体模型孤子波解

冯依虎 ，汪维刚，莫嘉琪

(1. 亳州学院电子与信息工程系，安徽 亳州 236800；2. 上海大学数学系，上海 200436；3. 合肥幼儿师范高等专科学校，安徽 合肥 230011；4. 安徽师范大学数学和计算机科学学院，安徽 芜湖241003)

近年来, 各类等离子体的研究已有很多论述，例如对激光等离子体，致密天体等离子体和尘埃磁等离子体等的特性的研究[1-9]。一些量子等离子声波与量子相关的特性也有很深入的讨论[10-11]。

当前许多学者对于非线性问题的解作了较多的探讨。莫嘉琪等[12-18]也利用一些渐近分析等方法讨论了一类非线性物理问题[19-39]。

本文是在具有电子和离子的情形下，讨论了温度梯度及其密度的量子等离子体系统。利用有关数学物理方法和理论，来探讨其非线性系统类孤子波解的性态。

1 量子等离子动力学模型

由量子等离子体动力学理论，在量子的碰撞频率比较低的时，一类非均匀量子等离子体非线性动力学模型为[17]

(1)

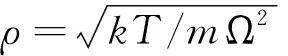
模型(1)是非线性偏微分数学物理方程。我们采用较特殊的方法来讨论方程(1)的扰动孤子波解。

(2)

现求非线性无量纲量子等离子方程(2)的孤子波解。引入行波变换:

(3)

(4)

这里

(5)

2 等离子体静电势零次孤子波

设非线性无量纲行波方程(4)的扰动解为

(6)

将(6)式代入行波方程(4)，按微扰参数ε展开非线性项，合并εi(i=0,1,)同次幂项， 并分别令它们的系数为零。由ε0的系数为零，得到非线性方程:

(7)

其中α,β,γ,κ由(5)式表示。

现利用双曲函数待定系数法求方程(7)的解。设方程(7)有孤子波解

(8)

其中Ai,Bi为待定常数。将(8)式代入非线性方程(7)，合并tanhτ的各正负次幂的系数，并分别设其为零，我们能决定系数Ai和Bi。再将得到的Ai和Bi代回(8)式，便有如下两个孤子波解：

(9)

v20(τ)=C0+C1(2-tanhτ)tanhτ

(10)

这里的常数C0,C1为:

(11)

取C0=0,C1=10。这时孤子波解(9)和(10)式分别描述了两个不同性态的奇异孤子v10，和v20正常孤子波解。如图1，2所示。

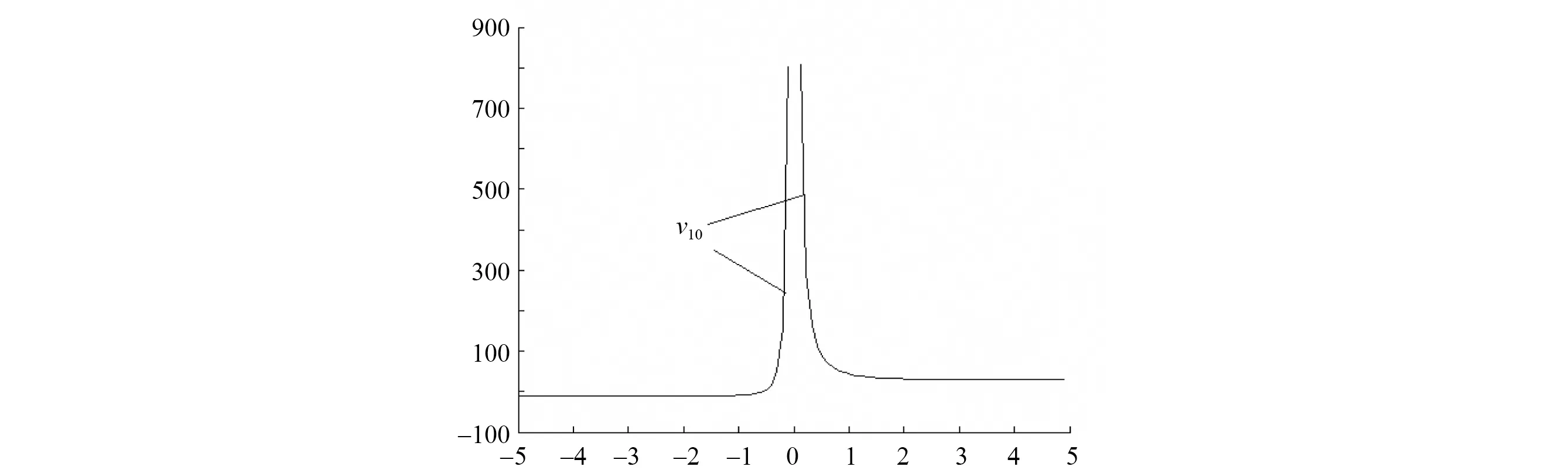
图1 量子等离子体静电势零次孤子波v10(τ)曲线(C0=0,C1=10)Fig.1 The zero-th solitary wave v10(τ) curve in quantum plasma electrostatic potential (C0=0,C1=10)

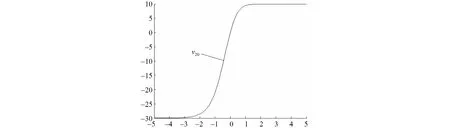
图2 量子等离子体静电势零次孤子波v20(τ)曲线(C0=0,C1=10)Fig.2 The zero-th solitary wave v20(τ) curve in quantum plasma electrostatic potential (C0=0,C1=10)

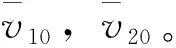
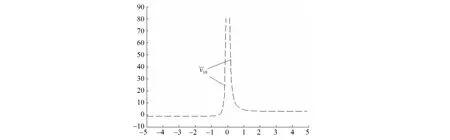
图3 量子等离子体静电势零次孤子波曲线(C0=0,C1=1)Fig.3 The zero-th solitary wave curve in quantum plasma electrostatic potential (C0=0,C1=1)

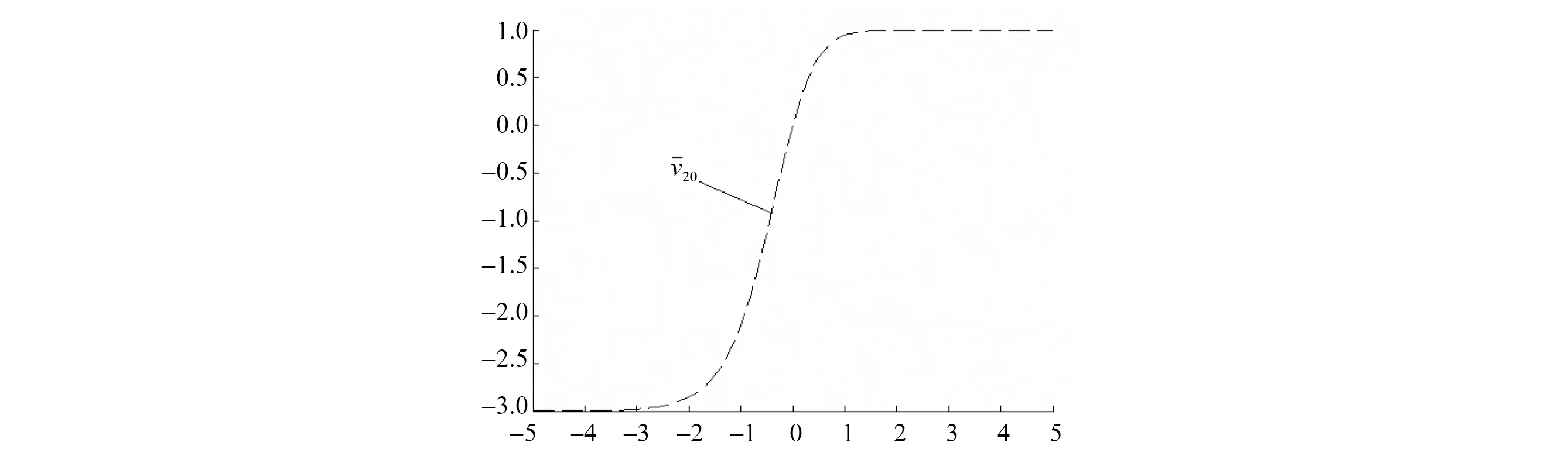
图4 量子等离子体静电势零次孤子波曲线(C0=0,C1=1)Fig.4 The zero-th solitary wave curve in quantum plasma electrostatic potential (C0=0,C1=1)

3 等离子体静电势的各次孤子波

将(7)式代入行波方程(4)，按微扰参数ε展开非线性项，合并εi(i=0, 1,)同次幂项。 由ε1的系数为零，得到线性方程:

(12)

其中v0是由(9)，(10)式决定的已知函数。由线性方程(12)可得到在零初值下的解v11(τ),v21(τ)。

于是由扰动理论和(7)式，我们可得到两个非均匀非线性无量纲量子等离子方程(4)静电势的一次近似的孤子波解v1(τ,ε),v2(τ,ε):

(13)

v2(τ,ε)=C0+C1(2-tanhτ)tanhτ+εv21(τ)+O(ε2), 0<ε≪1

(14)

取C0=0,C1=10。这时孤子波解(13)和(14)式分别描述了两个不同性态的孤子波静电势的一次扰动函数v11,v21。如图5，6所示。

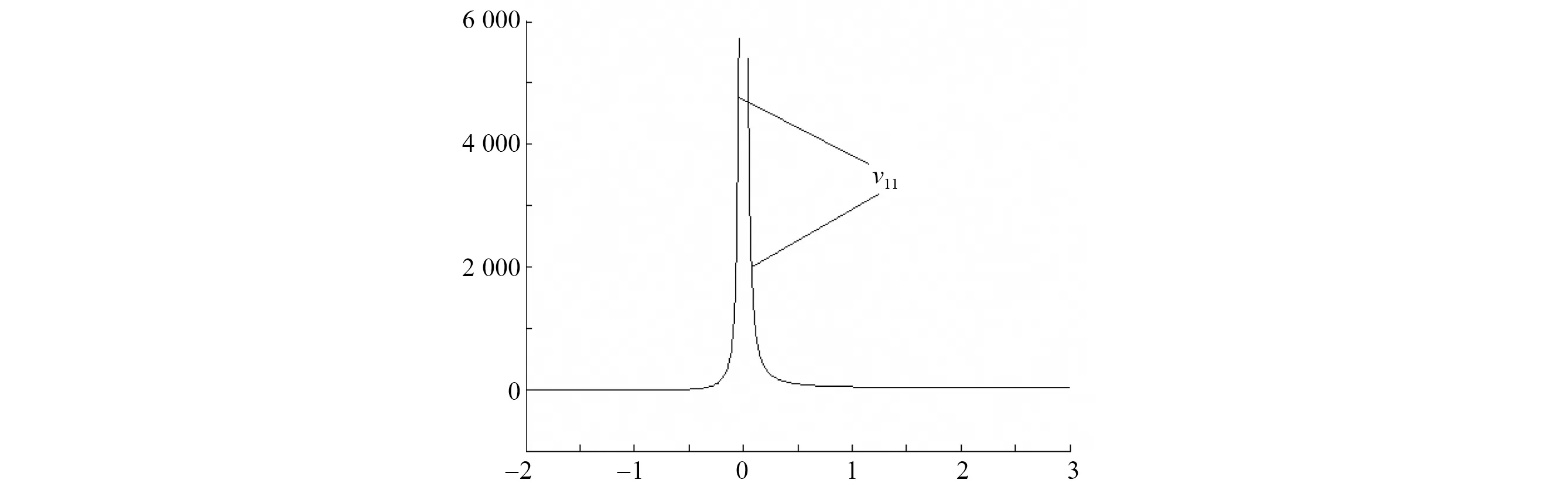
图5 量子等离子体静电势一次孤子波v11(τ)曲线(C0=0,C1=10)Fig.5 The first solitary wave v11(τ) curve in quantum plasma electrostatic potential (C0=0,C1=10)

图6 量子等离子体静电势一次孤子波v21(τ)曲线(C0=0,C1=10)Fig.6 The first solitary wave v21(τ) curve in quantum plasma electrostatic potential (C0=0,C1=10)

用同样的方法，由量子等离子体非线性动力学模型(4)的结构，可依次得到函数序列{v1n}和{v2n}。

由摄动理论知[12,40]，由(7)式决定的级数

在τ的有限区间内是一致有效的。即

于是v1n(τ,ε)以及v2n(τ,ε)就是方程(4)两个量子等离子体静电势孤子波的n次孤子波渐近近似解:

考虑到变换(3)，于是un(k1y1+k2z1-k3t1)就是量子等离子体非线性动力学无量纲模型(2)的两个静电势孤子波的n次行波解:

0<ε≪1,

0<ε≪1

4 等离子体的力函数孤子波

利用量子等离子体非线性动力学无量纲模型(4)的静电势孤子波扰动解，可以得到各类相关的物理量。例如由方程(4)和关系式(13)～(14)，不难得到量子等离子体非线性动力学无量纲的两个力函数的n次孤子波函数F1n(τ,ε),F2n(τ,ε):

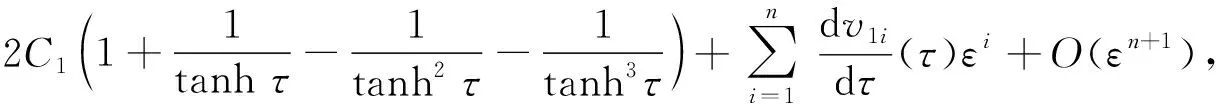
n=1,2,,0<ε≪1

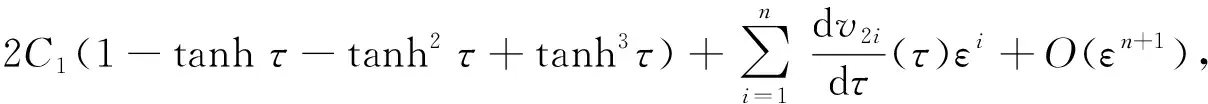
n=1,2,,0<ε≪1

取C1=10，这时量子等离子体非线性动力学无量纲的两个力函数的一次孤子波函数F11(τ,ε),F21(τ,ε)的曲线如图7，8所示。

图7 量子等离子体力函数一次孤子波F11(τ)曲线(C1=10)Fig.7 The first solitary wave F11(τ) curve in quantum plasma force function (C1=10)

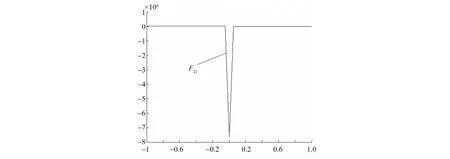
图8量子等离子体力函数一次孤子波F21(τ)曲线(C1=10) Fig.8 The first solitary wave F21(τ) curve in quantum plasma force function(C1=10)

5 结 论

通过非均匀量子等离子体系统的动力学方程，可以讨论该系统电势的冲击解、爆炸解和旋涡解等，并可分析电势的冲击波的幅度和爆炸波的宽度和密度与漂移速度的变化关系等。从而可了解静电势随时空的变化的稳定性状等物理性态。

非均匀量子等离子扰动系统出自于复杂的自然现象。为了研究非线性孤子波较复杂的模型，我们有时需要用近似方法去求解它。本文所用双曲函数待定系数和扰动理论方法就是一个有效的方法。用本文方法得到的解，还可进行解析运算。因此它可以继续研究孤子波解相关物理量的其它物理性态。