基于VMD和马氏距离SVM的滚动轴承故障诊断
2019-10-14乔美英刘宇翔兰建义
乔美英, 刘宇翔,兰建义
(1.河南理工大学电气工程与自动化学院,河南 焦作 454000;2.河南理工大学能源科学与工程学院,河南 焦作 454000;3.煤炭安全生产河南省协同创新中心,河南 焦作454000)
滚动轴承广泛应用于机械、电力、矿山及航空航天等行业中[1],是极易发生故障的零部件。轴承的运行状态直接影响到设备的安全与运行,对滚动轴承的运行状态进行检测并及时识别具有重要而深远的意义。在实际的应用中,轴承早期故障特征通常比较微弱;且振动传输路径的衰减影响、以及环境噪声的干扰均会对轴承振动信号的特征提取形成严重的阻碍[2]。因此,轴承的故障诊断为机械故障领域的研究热点与难点[3-4]。轴承的振动信号一般是非线性、非平稳的信号。针对噪声干扰下的非线性、非平稳信号,传统的振动信号分析方法,如傅里叶变换难以满足实际需要[5]。经验模态分解(empirical mode decomposition, EMD)[6]是一种新颖的时频分析方法,可直接根据信号本身的时间尺度特征进行分解,其结果具有较高信噪比和时频分辨率,因此被运用在滚动轴承的故障特征提取中[7-8],但其递归模式分解会导致估计误差不断传递,出现模态混叠等不良现象[9-10]。而变分模态分解(variational mode decomposition, VMD)采用非递归的处理策略,通过构造并求解约束变分问题来实现对信号的分解;相比于EMD,VMD可抑制或避免模态混叠现象,并且具有更高的运算效率及良好的噪声鲁棒性。赵洪山等[11]利用最大相关峭度解卷积对信号去噪,以峭度指标选取VMD分解后的模态分量,通过分析模态分量包络谱中幅值突出的频率成分判断轴承故障类型。Liu等[12]以峭度最大值为指标,确定VMD的二次惩罚项及分解模态数,利用变分模态分量的能量熵来检测铣削颤振。王新等[13]根据VMD分解的不同本征模态分量具有不同的频带能量,从故障信息的模态分量中提取特征,结合支持向量机来判断轴承的工作状态。张超等[14]将变分模态分解各模态分量的能量熵作为特征值,输入支持向量机中,进行轴承的故障诊断。然而,在以上支持向量机的核函数计算中,常常用欧氏距离来表示两个样本的距离,赋予每个变量相同的权重,忽略了各个变量间的相关性,所以不能准确地进行距离度量;而马氏距离[15]通过计算数据样本集之间的协方差距离,来度量两个样本之间的相似度,不仅不受特征量尺度的影响,而且能够考虑特征量之间的相关性干扰,因此被广泛用于样本的距离测量中[16-18]。
本文提出一种基于变分模态分解和马氏距离SVM的轴承故障诊断方法,简称VMD-MDSVM (mahalanobis distance support vector machine)。首先,采用小波软阀值去噪法对原始振动信号进行去噪,提取有效信号;其次,根据VMD不同模态分量的中心频率大小不同的特点,确定分解模态数;并将分解后的模态分量的能量作为故障特征,输入基于马氏距离高斯核函数的SVM中,进行故障诊断。实验表明,本文所提VMD-MDSVM方法可以迅速、有效地实现轴承的故障诊断。
1 小波去噪
在轴承振动信号的采集过程中,由于测量仪器的误差、测量精度以及环境的影响,使得采集到的信号中伴随着大量的噪声,掩盖了原始信号的特征信息,严重影响了轴承振动信号的分析以及轴承运行状态的辨别。近年来,小波分析方法[19]得到了快速地发展,小波阈值去噪具有良好的去噪效果,可以有效地提高信噪比。小波阀值去噪方法是根据信号在不同分辨率下呈现的规律特性, 在各种尺度下按照设定的阀值门限来调整小波系数, 进而完成去噪的数据处理方法[20]。其具体步骤如下:
(1)计算原始信号f(t)的小波变换。选择合适的小波基和小波分解层数,将f(t)进行小波分解,得到相应的小波分解系数wj,k;

(3)利用估计的小波系数进行小波重构,便可得到估计信号f′(t),即为去噪后的信号。
对小波系数进行处理一般采用硬阀值法和软阀值法。
硬阀值函数为

软阀值函数为


虽然硬阈值法在均方误差意义上要优于软阈值法,但是其信号会产生附加震荡和跳跃点,不具有原始信号的平滑性,而软阈值估计得到的小波系数整体连续性较好,从而使估计的信号不会产生附加震荡。因此,本文采用软阀值法对小波系数进行处理。
2 变分模态分解
变分模态分解(variational mode decomposition, VMD)是一种完全非递归、自适应和准正交的信号分解方法。该方法通过构造、迭代求解约束变分模型的最优解,来获取每个模态分量的频率中心及带宽,实现对信号的有效分解。假设欲将一个原始信号f分解为k个不同模态的固有模态函分量,则相应的变分问题构造过程如下。
(1)对于每一个IMF分量uk(t),利用Hilbert进行解调,得到其解析信号J(t)
(1)
其中,δ(t)是一个单位脉冲函数。
(2)将每个模态与指数项结合,对预估中心频率进行调整,把各个模态的频谱调制到相应的基频带上,即
(2)
(3)利用解调信号的H1高斯平滑指标,估计各个IMF分量的带宽,最终得到受约束的变分问题
(3)
式中,{uk}={u1,u2,,uk}为分解得到的k个IMF分量,wk表示所有中心频率的集合,即Wk={w1,w2,,wk}。
在求解该约束变分问题时,需要将原始约束问题转为非约束问题,为此引入二次惩罚项α及Lagrange乘子λ,引入的二次惩罚项α可以提高信号重构的准确度,Lagrange保证了约束条件的严格性。因此,原约束问题可转化为如下无约束问题。
L({uk},{wk},λ)

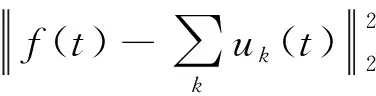
(4)

(5)

(6)

(2)根据式(5)和式(6)分别更新uk和wk。


(4)若满足迭代停止条件
则停止更新,输出其结果;否则返回步骤(2)。
3 基于马氏距离的SVM
支持向量机(SVM)是在统计学习理论的结构风险最小化的理论基础上发展而来的一种机器学习方法,其具有较强的学习能力与泛化能力,能够有效地解决小样本、非线性以及局部极值等问题,实现对样本的准确分类。
给定一个训练样本X={x1,x2,,xn}。其中,n为样本的长度,每个样本xi属于一个分类y∈{-1,+1},那么SVM原始模型可以表示为

s.t.yi[wφ(xi)+b]
≥1-εi,
εi≥0,
i=1,2,,n
(7)
其中,w为超平面的法向量,b/‖w‖决定了超平面的偏置量,εi为松弛变量,C是平衡因子。


dM(xi,xj)=(xi-xj)TM(xi-xj)
(8)
其中,矩阵M是一个半正定矩阵,称为马氏距离矩阵。对马氏距离矩阵M进行奇异值分解,可得M=AAT,因此,基于马氏距离的高斯核函数可以表示为:
(9)
式中,σ>0,σ为函数的宽度参数,控制了函数的径向作用范围。为了求解式(7),构建Lagrange函数如下:
L(w,b,φM,ε,α,β)

(10)
式中,αi>0和βi>0为拉格朗日乘子。由于映射函数φM中的两个参数A和σ一般是预先设置好的,因此可认为是一个常量,拉格朗日函数L(w,b,φM,ε,α,β)也可以写为L(w,b,A,ε,α,β)。公式(10)中的优化问题就可以转化为:

(11)
对L分别求(w,b,A,ε)的偏导数,并令其为零,即

(12)
将式(12)带入式(11)可得

(13)
从式(9)和(13)可以看出,有三个变量是未知变量,即支持向量机参数α、β和矩阵A。为了求解这三个参数,可以先固定矩阵A,求解关于α和β的子问题;再固定α和β,来求解关于矩阵A的子问题。通过交替更新α、β和矩阵A,优化问题最终达到收敛,就可以得到式(13)中的最优解。
公式(13)对α和β分别求偏导数,得到α和β的更新表达式,即

(14)
式(14)显然是一个二次规划问题,通常使用序列最小优化算法(sequential minimal optimization,SMO)[21]进行求解。求出α和β之后,对矩阵A进行更新。设定公式(11)对矩阵A的偏导数为0时,很难得到A的解析表达式。因此,本文通过梯度下降的方法对A进行更新。因在初始条件下,矩阵A是预先设置的,与最优值的差异可能较大,所以需要反复对α、β和矩阵A进行交替更新,以获取最优的矩阵A。
4 实验与分析
采用图1所示的动力传动故障诊断综合实验台(DDS)是一个完整的动力传动系统,由扭矩传感器、编码器、调速驱动电机、齿轮箱、可编程磁力制动器以及数据采集系统等组成,可以对磨损分析的齿轮箱诊断技术和振动特性等方面进行研究。本文运用该实验台进行轴承内外圈、滚动体故障以及轴承正常情况下的实验,安装在故障轴承端盖上的3个传感器用于采集振动信号。测点位置如图2所示,选择其中一个传感器的信号进行分析。在该实验中,滚动轴承型号为MBER16K深沟球轴承,其接触角为00,内径254 mm,外径51 mm,节径38 mm, 采样频率设为2 560 Hz,采集20 000个振动信号点。其中,每种轴承状况采集5 000个信号点。

图1 动力传动故障诊断综合实验台Fig.1 Drive train diagnostics simulator

图2 传感器测点布置Fig.2 Layout of sensor measurement points
由于采集的振动信号含有大量噪声,需采用db3 3尺度小波软阀值去噪法对原始振动信号进行分解与重构,以实现降噪。以外圈故障为例,去噪前后的信号如图3所示。从图中可以明显看出,大量的噪声信号已被滤除,波形变得更加光滑与清晰,说明去噪效果较好。

图3 去噪前后信号Fig.3 Noising and de-noising signal
对去噪后的信号进行变分模态分解,提取信号的各个变分模态分量以及相对应的中心频率。在VMD分解之前,需要先确定模态数k,k值偏大或偏小都会影响VMD分解的效果。由于每个模态的区分主要是由中心频率的大小决定的,可通过观察对比各个变分模态分量的中心频率的方法来确定k。
当出现中心频率较为相近的模态分量时,便可认为信号出现了分解。不同k值对应的中心频率如表1所示。

表1 不同k值所对应的中心频率Table 1 Central frequency of different k values
从表1中可以看出,当k=5时,有两个变分模态分量的中心频率为595和751 Hz,相距较近,可认为已出现过分解;当k=6时,其中两个变分模态分量的中心频率为585和686 Hz,相距更近。因此,模态数k选4较为合适。惩罚因子α设为默认值2 000,τ设置为0.2,以保证分解的保真度。
为了验证k=4是否合适,计算不同k值时VMD分解之后的各模态与原信号间的Pearson相关系数P,如表2所示。表2中,当k=5时,模态u5的Pearson相关系数为0.072 6,该值较小;当k=6时,模态u6的Pearson相关系数为0.050 3,该值也较小。这说明:当k大于4时,某些模态与原信号的相关系数将变得很小,可判断出该模态为虚假模态。

表2 不同k值下各模态与原信号间的相关系数Table 2 The correlation coefficient between the original signal and each mode under different k
同时,根据EMD利用正交性性能指标(index of orthogonality,简称IO)来定量分析原信号的分解精度。IO值越小,则表明原信号的分解精度越高,分解效果就越好。其中,正交性性能指标定义如下:
式中,L为信号的长度。
表3展示了在不同k值下VMD分解的IO值。可以看出,当k=4时,IO值最小;随着k值的增大或者减小,其IO值也相应的增大或减小。因此,可以判断出k值为4时较合适。

表3 不同k值下VMD分解的IO值Table 3 The IO of VMD decomposition under different k
采用EMD和VMD方法分别对去噪后的信号进行分解,VMD的模态数选为4;这是因为EMD分解后的能量主要集中在前几个分量中,所以选择前4个模态分量进行分析。图4和图5为分解后的时域图。观察发现,各IMF分量的时域波形差别不太大,根据波形很难直观的判断出哪一个分量的故障特征最明显。因此,需要观察分解后的模态分量的频谱,如图6和图7。
从图6和图7中可以看出,EMD分解后存在严重的模态混叠现象,而VMD有效地抑制了模态混叠,使得各变分模态分量集中在各中心频率附近,保留了模态分量的大部分能量,这说明VMD较EMD分解效果好。为了更加清楚地刻画各模态分量所含的故障信息,得到处理后各模态的包络图,如图8和图9所示。图中,VMD各模态分量均含有明显的故障特征;EMD各模态分量中也包含故障特征,但故障特征较不明显。这说明:在噪声的影响下,VMD可以更加有效地提取轴承的故障特性。但如果只利用VMD方法寻找故障特征频率,是不能满足要求的,因其无法准确区分同一故障状态下不同故障程度的故障特征。因此,本文从VMD中提取模态能量作为特征,采用马氏距离SVM对各种轴承运行状态进行识别。

图4 EMD的各模态分量的波形Fig.4 Waveform of each mode component of EMD

图5 VMD的各模态分量的波形Fig.5 Waveform of each mode component of VMD

图6 EMD的各模态分量的频谱Fig.6 Spectrum of each mode component of EMD

图7 VMD的各模态分量的频谱Fig.7 Spectrum of each mode component of VMD

图8 EMD的各模态分量的包络谱Fig.8 Envelope spectrum of modal components of EMD

图9 VMD的各模态分量的包络谱Fig.9 Envelope spectrum of modal components of VMD
提取上述4种轴承状况的数据,每种分为50组,各组数据信号点数为100,分别用EMD和VMD处理各组数据,并计算各个模态分量的能量,构成一个200×4的特征向量矩阵;针对每种轴承状况类型,选择34组数据作为训练集,16组数据作为测试集。分别采用EMD-SVM、EMD-MDSVM、VMD-SVM和VMD-MDSVM共4种方法对轴承数据进行分类识别,状态识别结果如表2所示。

表2 各诊断方法的识别准确率Table 2 Identification accuracy of diagnostic methods
从表2可以看出,相比于EMD-SVM 和EMD-MDSVM,VMD-SVM和VMD-MDSVM对轴承运行状态的识别具有更高的准确率;这是因为EMD在分解的过程中,会出现模态混叠现象且无法抑制,使得分解的结果不稳定与不唯一,不能有效地提取出信号的特征分量,进而影响SVM的分类准确度;而VMD算法对噪声具有较好的抗干扰能力,通过自适应分解,将信号在频域中从低频到高频逐次分离,分离出的变分模态分量可以克服模态混叠现象,因此实现了各分量的有效剖分,提取出了轴承运行状态的主要特征。此外,VMD-MDSVM在4种故障诊断方法中识别的准确率最高,比VMD-SVM高出3%;这说明采用马氏距离的SVM比传统的SVM方法分类效果更好,主要是因为在SVM的高斯核函数计算两个样本的距离时,马氏距离考虑了样本各个属性间的相关性,赋予其不同的权重,对两个样本的距离能更加准确地进行度量。
图10为4种方法对测试样本进行分类时的识别错误个数。从图10中可以明显看出,VMD-MDSVMD的识别错误数最少,仅在外圈故障和滚珠体故障样本中误识2个,说明VMD-MDSVMD的效果要优于其他算法;而EMD-SVM在轴承的每种状态下都出现了错误识别,错识样本数最多,达到了13个,效果最差。同时,EMD-MDSVM 和VMD-SVM在轴承的不同运行状态下,也出现了不同程度的错判,分别为5个样本和11个样本。另外,在四种轴承运行状态中,四种方法对轴承外圈故障样本都出现了错误判别,说明四种方法在识别轴承外圈故障时不够准确,还需再针对轴承外圈故障进行更加深入的研究。

图10 四种方法在轴承各运行状态下样本错识个数Fig.10 The wrong identification number of samples of four method in various running states of bearings
5 结 论
本文提出一种基于变分模态分解(VMD)和MDSVM的滚动轴承故障诊断方法。首先利用小波软阀值法对原始信号进行去噪,然后根据变分模态的中心频率确定分解模态数,最后将VMD分解后的变分模态能量作为特征向量样本,输入到马氏距离SVM中进行分类实验,并可得以下结论:1)小波软阀值去噪可有效地去除原始信号中的噪声信号;2)相比于EMD,VMD分解可有效的抑制模态混叠现象的发生;3)将马氏距离引入SVM核函数的距离计算中,可准确度量两样本的距离,提高SVM对轴承运行状态的识别率。但研究方法也存在不足,比如:在使用梯度下降法求解参数时,收敛速度慢,计算量大,使总的计算时间较长。在今后的研究工作中,需要寻找到一种更加先进的优化算法来提高计算效率。
