基于逐步优化算法的随机波浪荷载反演
2019-10-14叶静娴吕中荣汪利
叶静娴,吕中荣,汪利
(中山大学航空航天学院,广东 广州 510000)
海洋资源和能源越来越受到人们的重视[1-2]。与之相对应的海上结构,如海上采油平台、风力发电机等,因其所处的环境相当复杂,往往同时受到波浪荷载、风荷载、冰荷载等荷载的共同作用[3]。其中,波浪荷载是最主要的荷载[4]。考虑到波浪荷载的随机性和结构所处海洋环境的复杂性,波浪荷载难以直接实时测量,这将对海洋结构的设计和状态评估带来困扰。目前,结构响应的测量手段很成熟,如:加速度传感器可以直接提供加速度信息,应变片可以直接测量结构的应变。因此,可以海洋结构的实测响应为基础,反演得到波浪荷载。这一工作不仅能为海上结构的设计提供必要的荷载信息,同时也能为海上结构的运行监测和疲劳监测等创造条件。
根据响应反演结构所受荷载,是典型的反问题。国内外学者提出了一些波浪荷载的反演方法。Maes 等[5]基于一个风力涡轮机相似模型的加速度时程和动态模型,以递归联合输入状态估计算法反演了作用在其上的破波荷载、以及其他荷载,并进行了实验验证。Jensen等[6]利用ARMA校正模型,针对一个墩柱系统,以加速度作为输入,进行了系统参数识别和随机波浪荷载反演,并通过实验验证了该方法的有效性。王子健[7]第一次用全量补偿复合反演算法进行了桥墩的参数识别与波浪荷载反演,并结合概率论中的统计平均法与消去法,提出了改进的复合反演算法。以上方法大多将波浪荷载反演问题转化成一个状态估计问题,识别过程中将波浪荷载视为状态变量,然后采用滤波类方法进行状态变量估计。该类方法对于随时间变化缓慢的荷载识别问题较为有效,但如果荷载随时间变化较为剧烈,如:随机波浪荷载,该类方法将会产生较大的识别误差。本文提出了一种基于逐步优化算法的随机波浪荷载反演方法,该方法针对每两个相邻时间点建立目标函数,以加速度时程为输入,逐步识别一系列时间点上的波浪荷载,计算代价较低。该方法将荷载当作外部输入,而非状态变量,因此对时间变化剧烈的荷载如波浪荷载,仍能得到满意的识别结果。
1 基于波浪谱生成随机波浪荷载
Longuet-Higgins模型是常用的描述随机波浪的模型[8]。该模型认为,固定点的波面位置η(t)可看做是由许多不同振幅、不同周期和不同随机初位相的谐波迭加而成。

(1)
其中,t为时间;an为各组成波的振幅;ωn为圆频率;εn为随机初相位,它是均布于[0,2π]的随机变量。考虑到波面位置的随机性,通常使用功率谱密度函数Sηη(ω)描述波面位置的统计信息,即称为波面谱。本文考虑一种常用的P-M不规则波面谱[9],其表达式为:
(2)
其中,HS为有义波高。基于波浪荷载与波面位置的相关性,推导波浪荷载与波面谱的关系。考虑如图1所示小尺寸桩柱所受的波浪荷载,以海底为坐标原点,建立如下所示坐标系,根据Morison方程,z处的波浪荷载为:
f(z,t)=fD(z,t)+fM(z,t)

(3)


图1 圆管柱所受随机波浪荷载Fig.1 Random wave load on small pile column
根据波面函数(1),由线性波浪理论可得水质点速度和加速度的表达式如下:
(4)
其中,Tn为周期,满足Tn=2π/ωn,d为水深,kn为波数,满足以下色散关系:
ωn=gkntanhknd
(5)
进一步把Morison方程中的阻力项线性化处理,可得:
(6)
其中,σu(z)为速度的均方差,表达式如下:
(7)
由于k是ω的函数,它们满足式(5)中的关系,故式(7)不能通过直接积分求得。为简化起见,仅对上式波谱部分做积分,结合P-M谱,可得:
(8)
波浪荷载在柱高方向呈现出空间相关性,由式(3)和(4)可求得t时刻波浪荷载沿水深方向的分布,故可定出相应的空间分布系数。考虑水面下z1至z2处所受的合力,将波浪荷载沿着结构方向积分即可,再乘上相应的空间分布系数矩阵,即可得到各个自由度上的波浪荷载。通过积分得到总速度合力FD(t)和总惯性合力FM(t)如下:
(9)
以z1=0和z2=d代入上式进行积分, 并考虑色散关系以及σu的近似计算,由谱分析可得总速度力谱SFD(ω)和总惯性力谱SFM(ω)[10]。
(10)
相加即得总波浪荷载谱:
SFF(ω)=SFD(ω)+SFM(ω)
(11)
根据平稳随机过程的谐波合成法,波浪荷载F(t)可按如下方式生成[11]:
(12)

(1)划分频率区间的方法有等分能量法和等分频率法。在多数情况下宜采用前者,但对结构进行动力分析宜用后者。则上式中,Δω=(ωm+1-ω1)/m,m一般可取50~100,本文取50。

(3)频率范围ω1~ωm+1的选取, 在高频率和低频率段各舍去总能量的μ部分,这里μ取0.002。对于P-M谱有:
(13)
2 时程分析
多自由度系统的运动方程为:
(14)


(15)
其中, Δt是时间步长,参数γ和β在本文中分别取0.50和0.25。将式(15)代入(14)可得:
(16)
通过式(16),可由ti时刻的响应求得ti+1时刻的位移,将位移解代入(15)可求得ti+1时刻的加速度和速度如下:
(17)
循环以上步骤,可以求得所有离散时间点的位移、速度和加速度。
3 基于逐步优化算法的荷载反演方法
重新整合公式(16)和(17),可得状态方程如下:
xi+1=Hxi+G1Pi+1+G2Pi
(18)

(19)
其中,I为相应维度的单位矩阵。系统的观测方程如下:
yi+1=Lxi+1+M-1Pi+1
(20)
其中,yi+1表示ti+1时刻的测量数据,L为与实测结构响应相关的矩阵。本文主要考虑加速度测量数据,由式(14)可得L=[-M-1Κ,-M-1C]。
(21)
其中,λ是权值,其取值与测量误差水平有关。一般地,测量数据的误差越小,λ应越大;反之,λ则应越小。目标函数(21)是一个二次函数,其优化问题可直接求解,可得如下结果:
(22)
其中,矩阵A、b的表达式如下:
(23)
根据迭代式(23),最终可以逐个时间点识别波浪荷载。考虑波浪荷载具有一定的空间分布规律,将波浪荷载向量Pi用总波浪荷载Fi与空间分布系数矩阵Q的乘积来表示,即Pi=QFi。此时,迭代计算须用如式(24)-(25)替代。
(24)
(25)
在波浪荷载反演过程中,考虑波浪荷载的空间分布,能有效地缩减识别参数的个数,从而提高识别的精度。
4 算例验证
由于测量不可避免地存在误差,为了考察误差对反演算法的影响,在用Newmark-β法求得结构加速度时程后,添加一定水平的高斯白噪声,如下所示。
(26)


将含有不同程度噪声干扰的加速度时程作为输入,采用本文提出的荷载反演算法进行反演,识别出了两个自由度的荷载时程、速度时程以及位移时程,并进行误差分析。图3给出了无噪声情况下的反演结果。可以看出:当无噪声干扰时,波浪荷载的测量值与识别值几乎完全重合,这说明该反演算法在无噪声情况下是切实可行的。

图2 固定式海洋平台及其简化模型Fig.2 Fixed offshore platform and its’ simplified model
图4-5分别是噪声水平为5%和10%情况下的识别结果。由图4可见,在5%的噪声水平下,波浪荷载的识别值与测量值吻合很好,剔除几个极值点,其余点的识别结果的相对误差均小于1%。 由图5可见,在10% 的噪声水平下,剔除几个极值点,其余点的识别结果的相对误差均小于5%,满足工程需要。因此,该反演算法具有较强的抗噪声能力。

图3 无噪声情况下第二个自由度波浪荷载识别结果Fig.3 Wave force identified results of the second degree of freedom in the case of no noise interference

图4 噪声水平为5%时第二个自由度波浪荷载识别结果Fig.4 Wave force identified results of the second degree of freedom in the case of 5% noise level
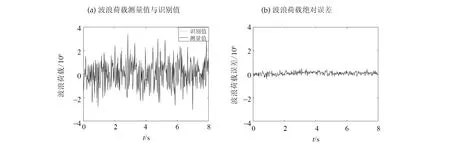
图5 噪声水平为10%时第二个自由度波浪荷载识别结果Fig.5 Wave force identified results of the second degree of freedom in the case of 10% noise level
5 结 论
本文提出了一种波浪荷载反演的逐步优化算法,该算法通过Newmark-β数值积分法将动力问题表达成状态方程,然后再基于每一个时间点建立目标函数,逐步识别波浪荷载。数值算例表明,即使在10%的噪声水平下,反演得到的波浪荷载仍具有很高的精度。
