相场方程指数时间差分法的能量稳定性分析

尹吉宪，张 鉴

1.中国科学院计算机网络信息中心，北京 100190

2.中国科学院大学，北京 100190

引言

微观结构的粗化动力学是指界面总能量降低所驱动的动力学过程，了解其机理和长期的统计对研究材料的力学性能具有重要意义。相场法已成为计算材料科学领域模拟和预测中尺度水平微观结构演化的一项通用性很强的计算方法[1]。相场法通过一系列不同的偏微分方程来反映有序化学势、热力学驱动以及扩散等物理机制的综合作用，并通过数值分析方法和计算机编程实现求解上述方程，从而得到体系的微观结构在时空上的瞬时状态[9]，进而分析和预测材料的性能。在相场模型中，常用的相场方程有用于反映成分变化的保守场变量演化过程的 Cahn-Hilliard 方程[2]，以及用于反映结构差异的非保守场变量演化过程的Allen-Cahn 方程[3]。在本文中，不仅仅涉及了 Allen-Cahn 方程和 Cahn-Hilliard 方程，我们对它们的耦合模型也进行了讨论。对于这些偏微分方程的数值解的求解方法通常有显式、隐式的时间差分格式等，但是这些方法很难设计出能量稳定、大时间步长的求解格式。在本文的工作中，我们对 Allen-Cahn 方程、Cahn-Hilliard 方程以及它们的耦合模型，介绍了一个快速且稳定的紧致指数时间差分的解法[4][12]。同时，对于这三种模型的紧致指数时间解法，我们也讨论了它们的能量稳定性证明。相比于显格式求解方案的能量稳定性证明[8]，紧致指数时间差分方案在能量稳定性证明上有独特之处，它需要针对积分因子项进行特别处理。又区别于王奇教授在具有非局部约束的相场模型的线性二阶能量稳定格式[11]中所作的工作，本文是基于原自由能函数的完全离散能量稳定性的证明。在完成能量稳定性证明之后，我们设计了数值实验，验证了紧致指数时间差分方案相比于显格式在大时间步长上的优势。

1 紧致指数时间差分法简介

1.1 相场方程

在本文中，我们考虑 Allen-Cahn 方程和 Cahn-Hilliard 方程的耦合模型：

其中 Ω 是Rd中的一个矩形区域，t0是起始时间，T>0 是微结构演化的持续时间，α1、α2是正数。为了求 (1.1) 的数值解，我们首先赋予 (1.1) 在区域 Ω 上初值条件η|t=t0和c|t=t0，同时赋予 (1.1) 的边界条件——周期边界条件。我们定义与 (1.1) 相对应的自由能函数如下：

至于单独的 Allen-Cahn 函数：

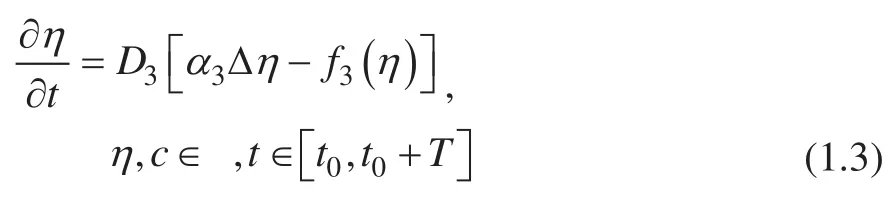
其相应的自由能函数为：

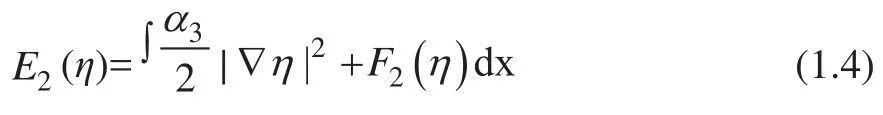
至于单独的 Cahn-Hilliard 函数：

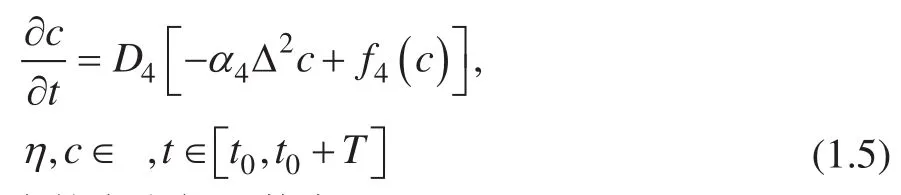
其相应的自由能函数为：

1.2 紧致指数时间差分格式

接下来，我们介绍求解 (1.1) 的完全离散和能量稳定的紧致指数时间差分 (ETD) 求解格式。我们首先对 (1.1) 采取在传统的稳定半隐式方法中常用的线性分裂格式[5–7]，得到如下结果：

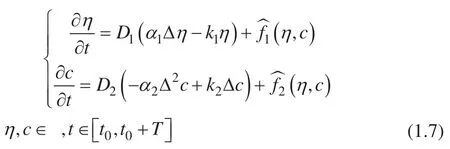
为了设计完全离散的 ETD 求解格式，我们首先离散求解区域和求解的时间长度。假定我们把求解区域离散为一个Nx×Ny网格 Ωh：，其中我们设。假定周期边界条件如下：

同时，我们定义矩阵 A、B和算子

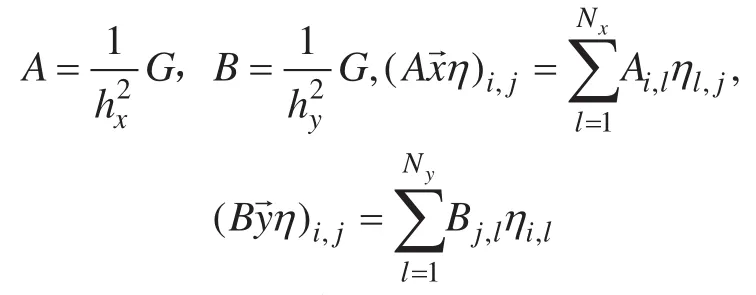
我们可以发现，矩阵A和B可以进行对角化分解，

其中Dx和Dy是对角矩阵，对角线上的元素分别为：

而Px、Py中的元素分别为：

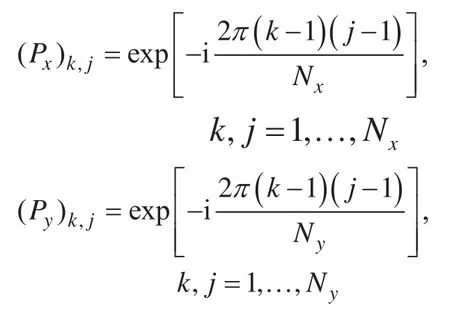
其中i是虚数单位。对于任意的二维矩阵f，我们可以证明是对二维矩阵f的每一列进行了离散的傅里叶变换，是对二维矩阵f的每一行进行了离散的傅里叶变换，而是对二维矩阵f的每一列进行了离散的逆傅里叶变换，是对二维矩阵f的每一行进行了离散的逆傅里叶变换。在第二部分证明能量稳定性的时候会用到这个性质。

同时我们也可以发现，算子x→、y→ 满足交换律，即：

为了设计全离散的 ETD 求解格式，我们首先离散拉普拉斯算子、梯度算子和散度算子。对于任意的二维矩阵f，g，f1，f2和任意的二维矩阵F=(f1,f2)T，离散梯度算子、离散散度算子和离散拉普拉斯算子定义如下：

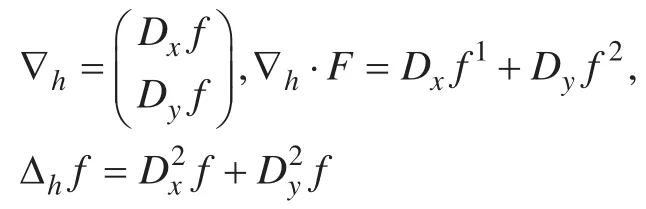
接下来我们对 (1.7) 进行空间上的离散，可以得到：

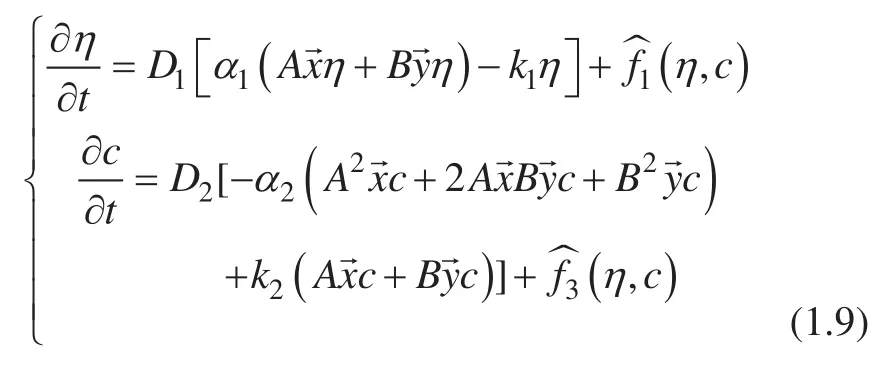
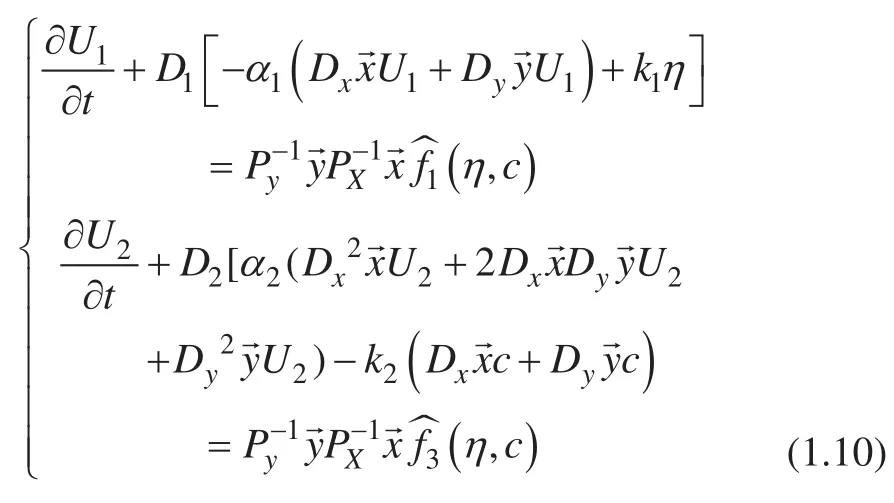
很明显，当k1和k2大于 0 时，我们定义算子e*、⊙ 如下：

通过定义的这两个算子，(1.10) 可以转换为：

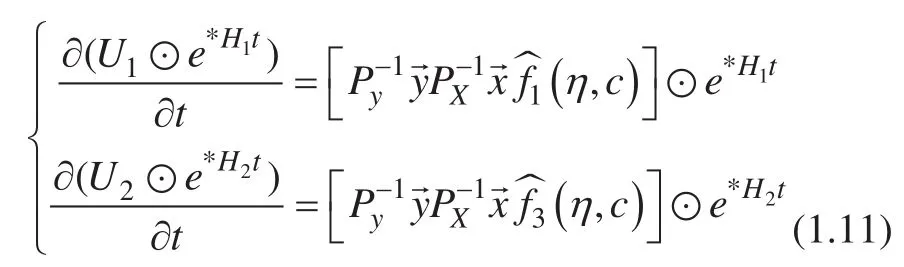
到目前为止，我们完成了空间离散，接下来我们进行时间离散，把T离散为单位时间长度 Δ=t/TNt。我们把方程组 (1.11) 的等号两边同时从tn到tn+1进行积分，可以得到：

通过(1.12)，我们可以得到

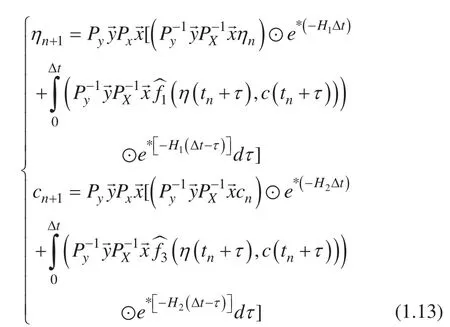
我们用拉格朗日多项式近似来估计 (1.13) 等号右边的积分部分，由此我们得到 ETD 求解格式：

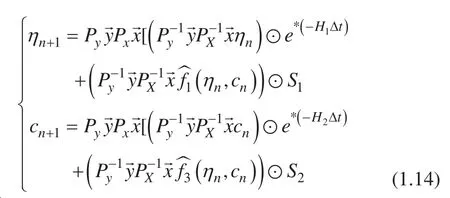
其中，

到目前为止，我们介绍完了 Allen-Cahn 方程和Cahn-Hilliard 方程的耦合模型的 ETD 求解格式。类似于上面的推导过程，我们可以推导出 Allen-Cahn 方程(1.3) 的 ETD 求解格式：

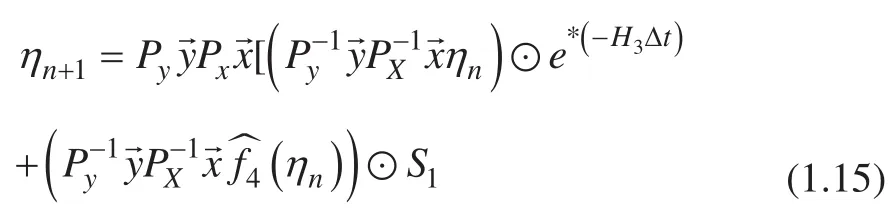
其中，

同样的，我们可以推导出 Cahn-Hilliard 方程(1.5) 的 ETD 求解格式

其中，

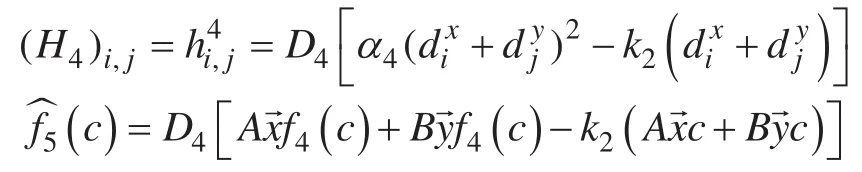
2 能量稳定性证明

我们已经得到了 Allen-Cahn 方程、Cahn-Hilliard方程以及它们的耦合模型的完全离散形式的 ETD 求解格式。在这一部分，我们将证明我们所得到的 ETD求解格式是满足无条件能量稳定的。

我们已经定义了离散的梯度算子、散度算子和拉普拉斯算子，现在我们定义离散的积分算子 ∑Ωh和L2模 ||·||h。对于任意的二维矩阵和任意的二维矩阵，我们定义离散的积分算子 ∑Ωh和L2模 ||·||h如下：

接下来我们将能量函数E1(η,c)，E2(η) 和E3(c) 离散成如下的形式：

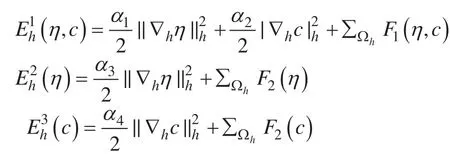
为了完成能量稳定性的证明，我们首先介绍几个引理。在这之前，我们假设根据之前的介绍，我们知道Tf是对f进行了二维离散的傅里叶变换。在接下来的证明中将用到这个性质。

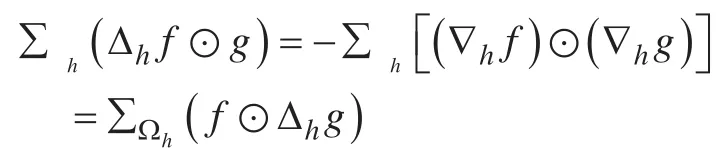
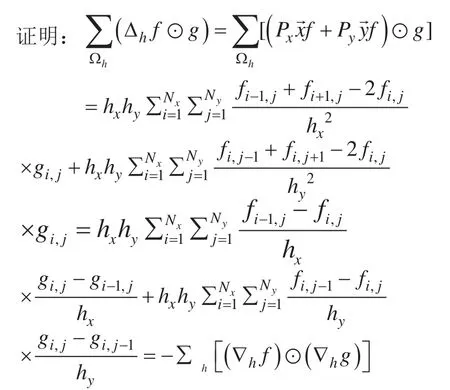
根据相同的推导过程，我们可以得到

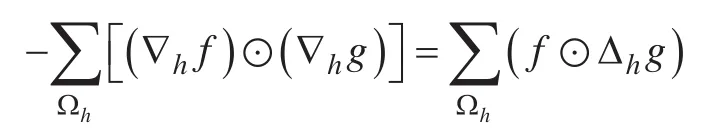
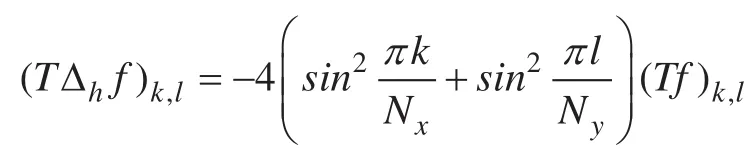
证明：。我们首先处理TfB这一部分。

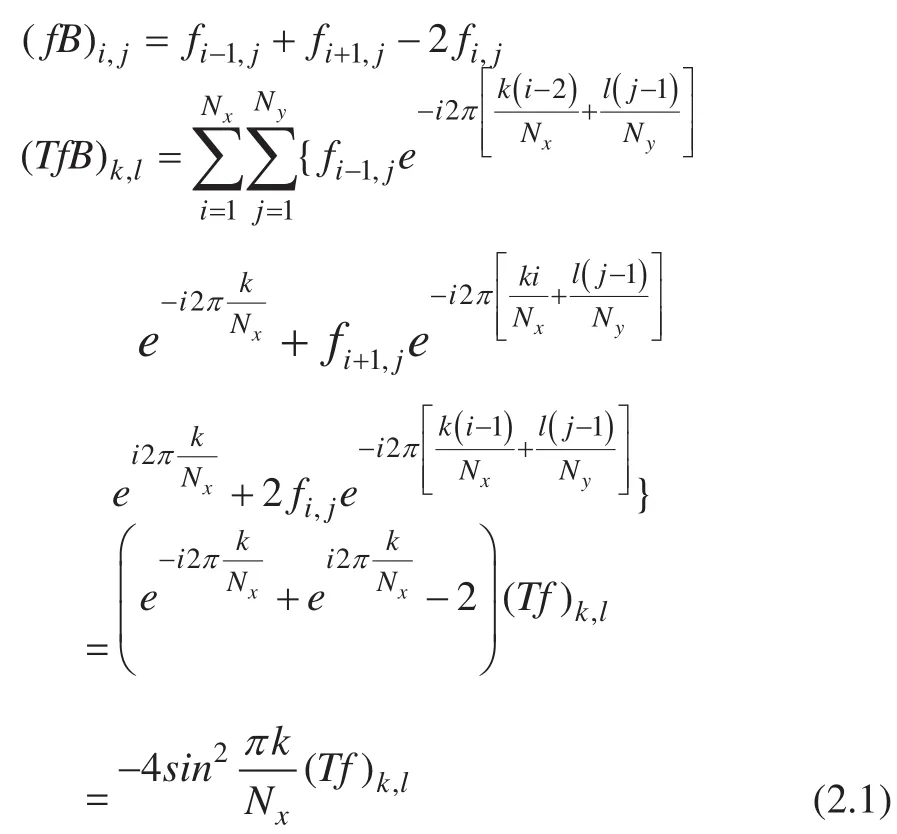
根据相同的推导过程，对于TfA，我们可以得到：

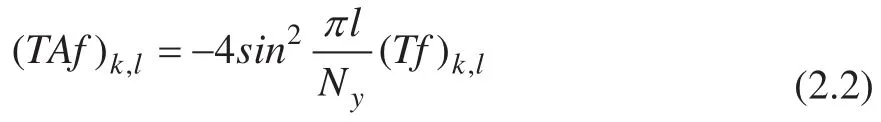
我们将 (2.1) 和 (2.2) 相加，得到

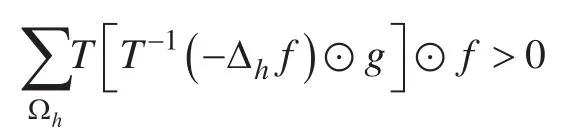
证明：根据帕塞瓦等式以及Lemma 2.2

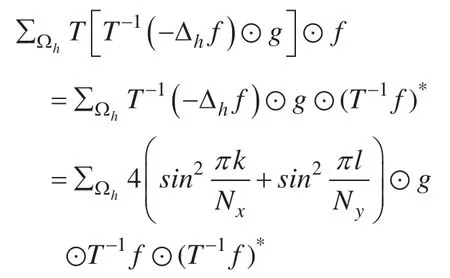
其中 (T-1f)*是T-1f的共轭复数矩阵，所以。又因为gi j,＞0，所以。

接下来，我们证明在第一部分中所介绍的 ETD求解格式是满足能量无条件稳定的。

Theorem 2.5 对于 Allen-Cahn 方程，ETD 求解格式 (1.14) 满足能量下降准则，即：，如果。

证明：根据 Allen-Cahn 方程的 ETD 求解格式(1.14)，我们可以得到

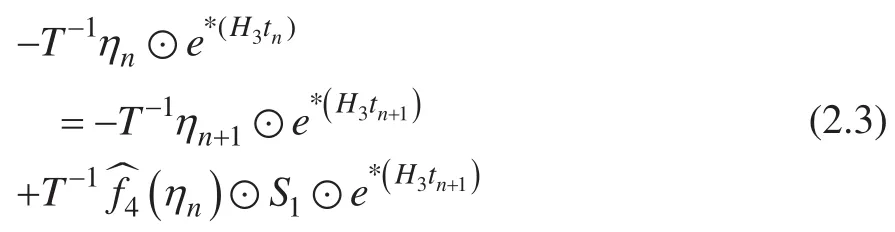
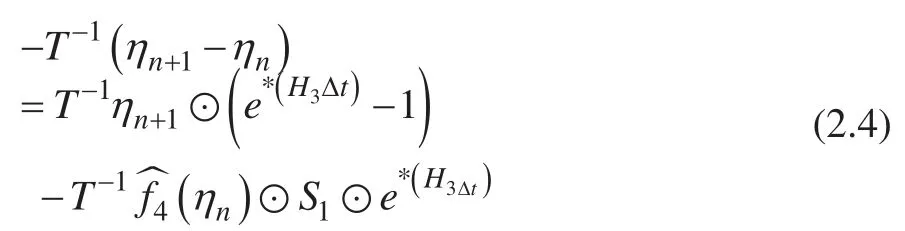
根据ex的泰勒展开式

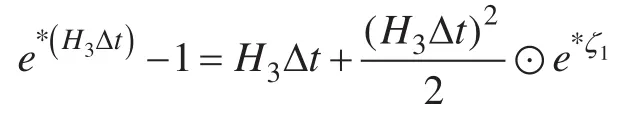
我们可以得到

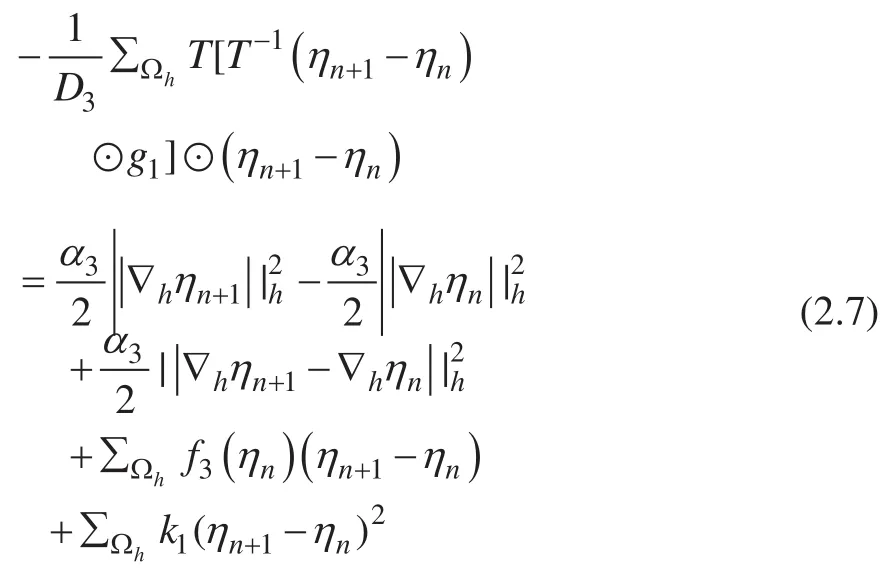
当F3(ηn+1) 在ηn处进行泰勒展开

我们可以得到

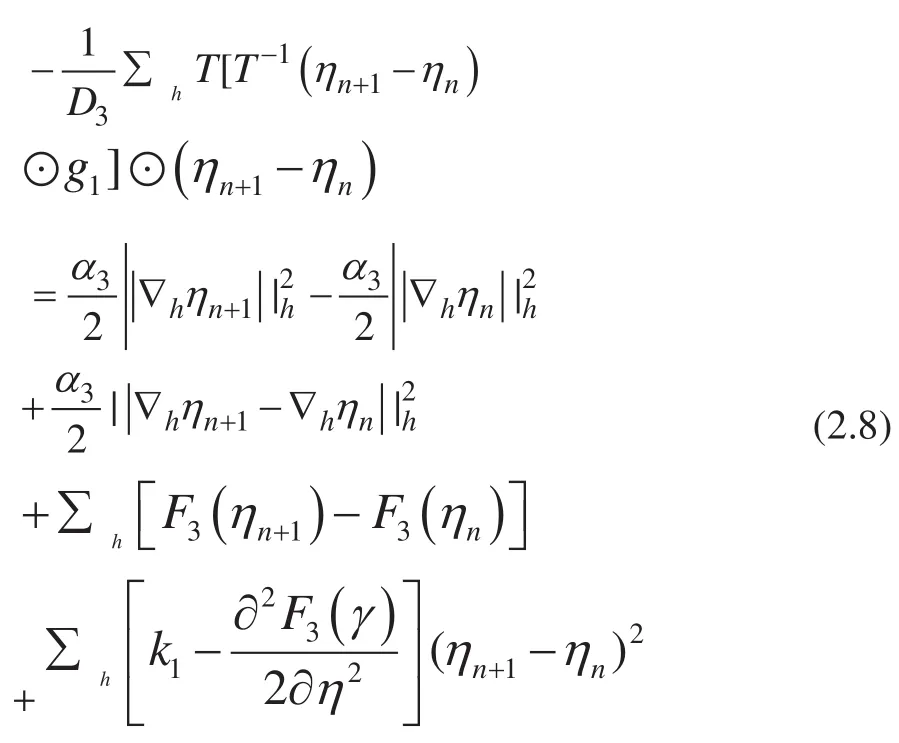
根据 Lemma 2.3，等式 (2.8) 等号左边小于 0，所以我们可以得到，如果，Allen-Cahn 方程的 ETD 求解格式就满足无条件能量稳定原则，即

Theorem 2.6 对于 Cahn-Hilliard 方程，ETD 求解格式 (1.15) 满足能量下降准则，即：，如果。

证明：类似于 Allen-Cahn 方程 ETD 求解格式能量稳定性的证明，在进行转换之后，我们可以得到

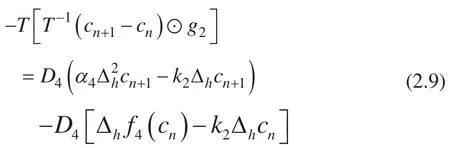
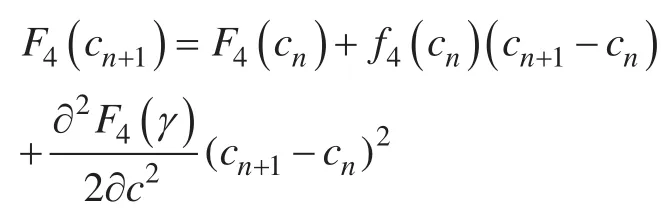
我们可以得到

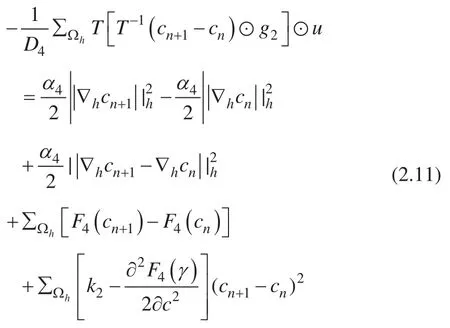
根据 Lemma 2.3，等式 (2.11) 等号左边小于 0，所以我们可以得到，如果，Cahn-Hilliard 方程的 ETD 求解格式就满足无条件能量稳定原则，即。

Theorem 2.7 对于 Allen-Cahn 方程 Cahn-Hilliard方程的耦合模型，ETD 求解格式 (1.13) 满足能量下降准则，即：，如果

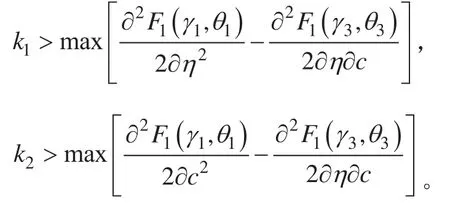
证明：类似 于Theorem 2.5 的证明，耦合模型中的 Allen-Cahn 方程部分，经过推导，可以得到：

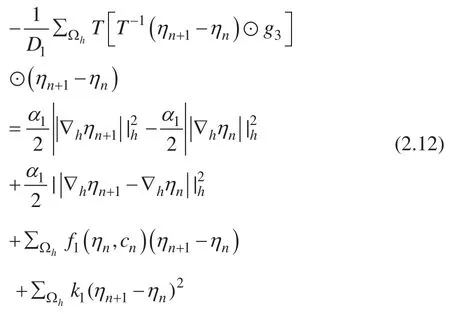
类似于 Theorem 2.6 的证明，耦合模型中的Cahn-Hilliard 方程部分，经过推导，可以得到：

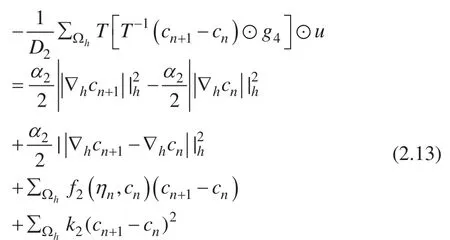
我们将等式 (2.12) 和 (2.13) 等号左右两边分别相加，可以得到：

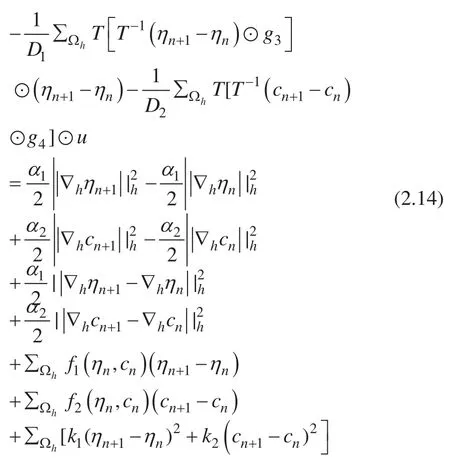
我们可以得到

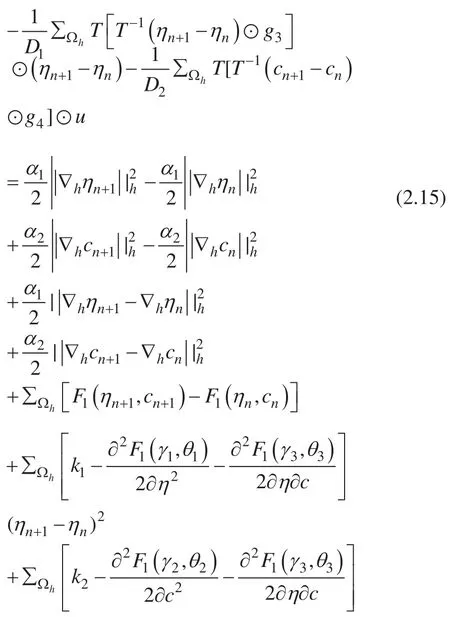
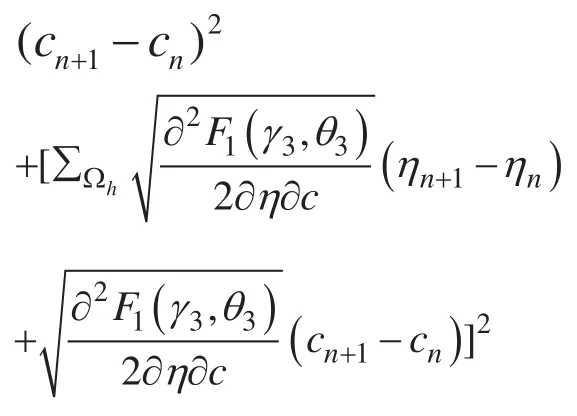
根据 Lemma 2.3，等式 (2.15) 等号左边小于 0，所以我们可以得到，如果

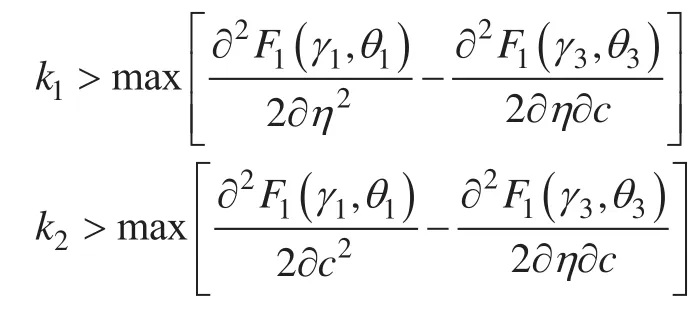
3 数值实验

在这一部分，我们将采取一系列的数值实验去验证我们所研究的 Allen-Cahn 方程、Cahn-Hilliard 方程以及它们的耦合模型的时间收敛率和能量稳定性。

3.1 Allen-Cahn 方程

对于 Allen-Cahn 方程 (1.3)，我们设定计算区域为Ω=[0,0.5π]2，将计算区域划分为的网格。同时，其他的参数设定为：α3=0.02、D3=1。对于Allen-Cahn方程的模拟，我们分别取 Δ t =δ，2δ，4δ，8δ，16 δ，32 δ，64 δ等七组数据 (其中 δ= 1× 10-3) 以同一初值运行到相同的时刻T。最后我们以更小的时间步长Δt=2× 10-4，用显格式的方法同样运行到相同的时刻T，作为基准解，与上述的七组结果进行对比，得到相对L2误差以及对应的收敛率如表3.1所示。通过表3.1，我们可以看出该 ETD 求解格式是一阶的。

3.2 Cahn-Hilliard 方程

对于 Cahn-Hilliard 方程 (1.4)，我们设定计算区域为 Ω=[0,2π]2，将计算区域划分为的网格。同时，其他的参数设定为：α3=0.02、D3=1。对于 Cahn-Hilliard 方程的模拟，我们分别取 Δt=δ，2δ，4δ，8δ，16δ，32δ，64δ等七组数据 (其中δ=2×10-6) 以同一初值运行到相同的时刻T。最后我们以更小的时间步长Δ=×t4 10-7，用 ETD 求解的方法同样运行到相同的时刻T，作为基准解，与上述的七组结果进行对比，得到相对L2误差以及对应的收敛率如表3.2所示。通过表3.2，我们可以看出该 ETD 求解格式是一阶的。同时，经过测试，对于该 Cahn-Hilliard 模型，为了保证能量不发散，显格式能采取的最大时间步长为 Δ=×t1 10-9。从中我们可以看出本文介绍的ETD求解方法在可采取的时间步长上是显格式的几千倍到几万倍。

3.3 耦合模型

在这部分的测试中，对于 Allen-Cahn方程和Cahn-Hilliard 方程的耦合模型，我们采取的具体算例[10]为：

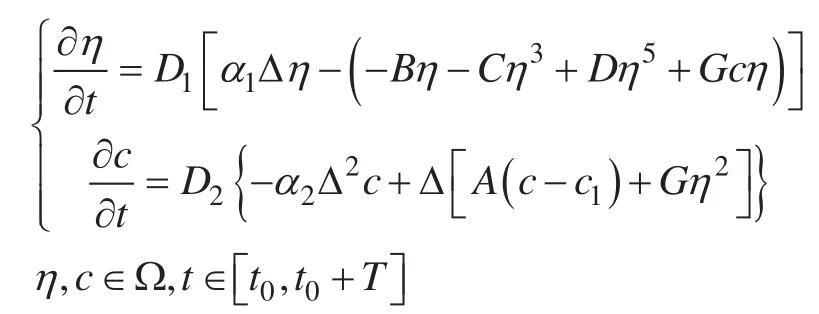
表1 一阶 ETD 求解格式的相对 L2 误差Table 1 Relative L2 Error of First Order ETD Solution Scheme for Allen-Cahn Equation

表2 Cahn-Hilliard 方程一阶 ETD 求解格式的相对 L2 误差Table 2 Relative L2 Error of First Order ETD Solution Scheme for Cahn-Hilliard Equation

表3 耦合模型一阶 ETD 求解格式中 η 的相对 L2 误差Table 3 Relative L2 Error of η in First Order ETD Solution Scheme of Coupled Model

表4 耦合模型一阶 ETD 求解格式中 c 的相对 L2 误差Table 4 Relative L2 Error of c in First Order ETD Solution Scheme of Coupled Model

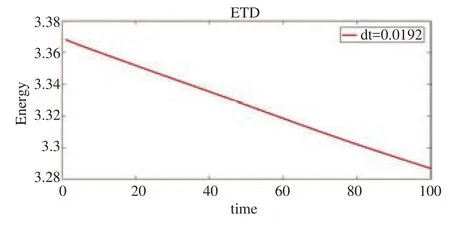
图1 耦合模型能量随时间变化Fig.1 Energy Changes with Time in Coupled Model

4 结语

对于矩形区域的 Allen-Cahn 方程、Cahn-Hilliard方程以及它们的耦合模型，本文介绍了一种快速稳定的紧致指数时间差分法。该方法通过采取线性分裂的方案来保障能量稳定性。对于该方法符合完全离散的能量稳定性原则，我们给予了严格的数学证明。相比于显格式求解方案能量稳定性的证明，本文对于紧致指数时间差分方案的能量稳定性证明，采用独特的方式处理了积分因子那一项。同时我们对于 Allen-Cahn方程和 Cahn-Hilliard 方程的耦合模型，我们也采用类似的方式和技巧证明了它的能量稳定性。同时我们通过数值实验证明了该方法相较于显格式，具备稳定、大时间步长的优势。下一步的工作将尝试探索更高阶的紧致指数时间差分的解决方案，以及该方案的能量稳定性的证明。