聚焦变式,激发思维
2019-10-11江苏省江阴市成化高级中学
☉江苏省江阴市成化高级中学 王 勇
在数学教学中,我们经常会遇到一类学生能听懂却不能独立完成的所谓难题,如何让这类问题变得容易,这一直困扰着教师和学生.笔者认为,教师在教学中应该帮助学生架“梯子”,让问题的难度“拾阶而上”,这样学生的思维就会爬得更高.笔者曾经上过一节《基本不等式的应用》的公开课,借助一道典型例题,从字母代换、结构调整、定值变换、类比猜想及定理性质的运用等多角度变式,探究知识发生的过程,揭示知识之间的联系,剖析问题的难易关系,培养学生的发散思维,从而建立化归思想,提高分析问题、解决问题的能力.下文就是这节课的大致过程,供同仁参考.
一、给出例题,多法证明
引例已知x>0,y>0,求证:
请同学们运用比较法、综合法、分析法分别对引例进行证明.六分钟后请学生交流(限于篇幅交流过程这里略).
设计意图:要求学生利用三种不同的方法加以证明,是为了让学生掌握证明不等式的三种基本方法,从而为下面的变式证明打下基础.
二、提出问题,引发探究
师:若a>0,b>0,c>0,则根据上面的引例,你能得出哪些结论?
生4:由上面三位同学的结论,我得到了新的结论:若a>0,b>0,c>0,则
生5:我对引例进行了变式,设x=a-b,y=b-c,则有x+y=a-c,于是得到如下结论:若a>b>c,则即
师:同学们回答得不错!从刚才大家得到的结论可以看出,对数学复杂问题的研究往往是从简单问题入手的,由此可见,打好基础是万里长征的第一步.
设计意图:引例其实是为学生搭建的“梯子”,顺着梯子往上爬,学生不仅看到了数学的“无限风光”,而且还培养了他们的探究性思维.
三、变式例题,激发思维
变式1:已知x>0,y>0,求使得恒成立的n的最大值.
请大家思考一下,如何解决这个问题?
师:再设a+b+c=1,则可得如下变式:
变式2:已知a,b,c是互不相等的正实数,且a+b+c=1,求的取值范围.
变式3:已知a>0,b>0,c>0,且a+b+c=1,求证
此变式请同学们课后自行证明.
设计意图:通过教师架梯,师生互动,进一步创设积极的探究氛围,从而激活学生的思维,并将学生的思维引向一个新的高度.
四、再变引例,优化思维
师:一题多解,是数学解题过程中的一大奇观,多题一解,一题多变,也是数学中常见的奇特现象.在引例中,若设x+y=1,我们可得如下变式:
变式4:已知x>0,y>0,且x+y=1,求证:
这道题的证明留给同学们课后完成,这里老师要请问同学们,你们能变式出相关的问题吗?
师:的确如此!请同学们课后完成:已知a>0,b>0,且a+b=1.求证
生12:老师,我也有发现!已知a>0,b>0,且a+b=1.求证本题除了转化为上题证明,还可以用三角换元进行证明,具体步骤如下:
设a=cos2α,b=sin2α,则有:
生13:我也发现了一个新题:已知a>0,b>0,且a+b=1.求证:
本题可以这样证明:由条件a>0,b>0且a+b=1,可得0<ab≤
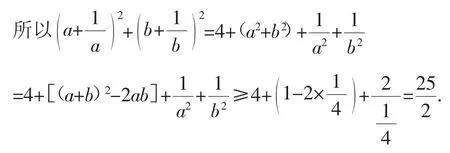
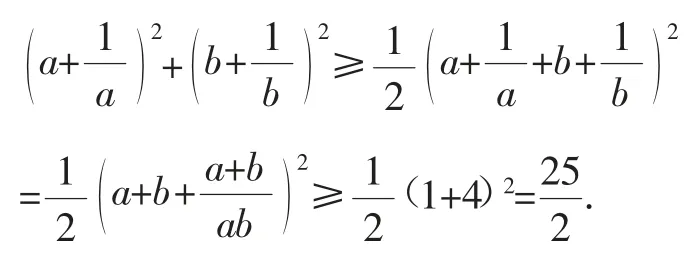
设计意图:继续架起思维的“梯子”,把学生的思维引向更高层次,让他们自己发现问题,并解决问题,以此来培养学生的数学核心素养.
从本课的设计可以看出,每一个难题不是凭空出现的,而是建立在一个简单问题的基础上,教师在数学教学过程中,应教会学生善于发现规律、掌握规律,真正做到举一反三,触类旁通,那么教学效率必然会大大提高.教师在教学过程中,要认真研究教科书中的每一个知识点,并且上升到一定的高度,只有这样,才能让自己的教学达到“源于课本,高于课本”的理想境界.
