例说多变量问题的处理策略

☉江苏省海门中学 汤晓玲

多变量问题是近年高考中的热门考题，也是高中数学中较难处理的问题，往往得分较低.从内容上看，多变量问题涉及的知识点多，覆盖面广，综合性强；从题型上看也是常考常新，解法灵活.面对这类问题时，许多学生望而生畏，完全找不到求解这类问题的突破点.本文通过几道典型例题的解答，介绍多变量问题的几种常规的处理策略.

一、基本不等式

例1已知正数x，y满足，求x+2y的最小值.

分析：抓住已知条件中的定值，将所求的x+2y配凑成与已知条件相关的形式.

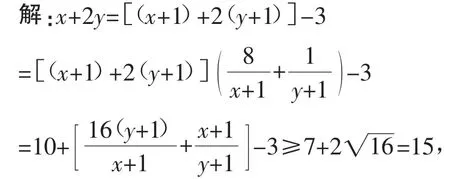
若已知条件中有定值，可以对所给的条件或结论进行适当的变形（因式分解、多项式展开等），寻找两者之间的联系，配凑出定值，利用基本不等式解决.

二、换元法

例2已知正实数x，y满足，则xy的取值范围是______.

分析：将xy换元成t，抓住已知条件中的定值，进而将其转化为求t的取值范围.

解法一：令t=xy，则

解法二：由解法一可得

三、主元法

例3设x1，x2，x3是三个互不相等的实数，若x1x2+x2x3+x3x1=-24，且x1+x2+x3=-3，则x1x2x3的取值范围是______.

分析：注意到x1，x2，x3完全等同的地位，可以把x1+x2和x1·x2表示成x3的函数，根据一元二次方程有两个不等实根，进而求出x3的取值范围，进一步求出x1x2x3的取值范围.

解：由已知条件得

所以x1，x2是方程x2+（3+x3）x+x32+3x3-24=0的两个不等实根.

从而Δ=（x3+3）2-4（x32+3x3-24）＞0⇒-7＜x3＜5.

令f（x）=x3+3x2-24x（-7＜x＜5），则f′（x）=3x2+6x-24=3（x+4）（x-2）.

令f′（x）=0得x=-4或x=2.

列表得：

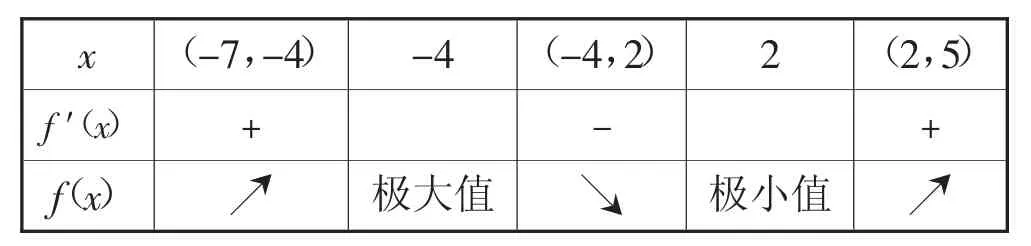
当x=-4时，f（x）取得极大值80，f（x）在x=2处取得极小值-28.

检验：①当x3=-4时，

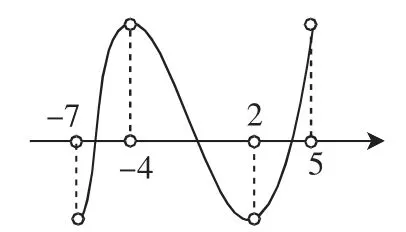
图1

所以x1，x2是方程x2-x-20=0的两个不等实根5，-4.

与已知x1，x2，x3是三个互不相等的实数矛盾.

②当x3=2时

所以x1，x2是方程x2+5x-14=0的两个不等实根-7，2.

与已知x1，x2，x3是三个互不相等的实数矛盾.

所以-7＜x3＜5且x3≠-4且x3≠2，又f（-4）=80=f（5），f（-7）=-28=f（2），所以-28＜f（x）＜80，从而x1x2x3的取值范围是（-28，80）.

本题中x1，x2，x3的地位完全等同，也可以转化成关于x1，x2的函数来处理，特别要注意题目中的陷阱，三个数互不相等，所以最后答案是开区间（-28，80）.有些问题中如果把涉及的常见变量字母（如“x”）当作主元，那么解题过程会比较烦琐，甚至无法求解.因此，根据解题的需要，必要时尝试换个角度来审视题意，或许就会豁然开朗.

例4若关于x的方程x2+ax+b=0有不小于2的实根，则a2+b2的最小值为______.

分析：如果直接从方程x2+ax+b=0有不小于2的实根出发，根据该方程在［2，+∞）上实根的个数进行分类讨论，并作出所得不等式组所表示的平面区域，这样相对来说比较烦琐.其实倘若注意到原方程是关于a，b的二元一次方程，故可以尝试以a，b为主元，x为次元，那么xa+b+x2=0可以看做是关于a，b的直线方程，a2+b2的几何意义是该直线上的点到原点的距离的平方，故可以将此最小值表示为关于次元x的函数表达式，最后求得此函数的最小值.

解：原方程可看做关于a，b的直线方程l：xa+b+x2=0，a2+b2的几何意义是直线l上的点（a，b）到原点（0，0）的距离的平方，故

本题的审题角度较为新颖，解题过程更为简洁.事实上，在多变量问题中，主元和次元是相对的，必要时可以相互转化，从而实现抓住关键、化难为易的目的.

四、数形结合

如果满足条件的多变量问题的约束条件可以用几何图形来表示，则可以挖掘待求问题的几何意义，并利用数形结合思想来求解.

例5在平面直角坐标系xOy中，过点P（-5，a）作圆x2+y2-2ax+2y-1=0的两条切线，切点分别为M（x1，y1），N（x2，y2），且，则实数a的值为______.

分析：注意到这个条件，可以联想到斜率公式，利用三点共线来解决.

解：记圆心为C，MN的中点为Q（x0，y0），圆C的方程为：（x-a）2+（y+1）2=a2+2.

因为MN⊥PQ，设A（1，0）.

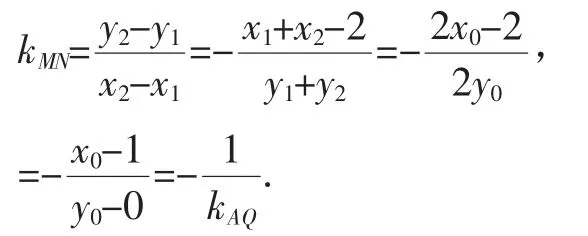
图2

所以P、A、Q、C四点共线.

在多变量问题中，若问题条件的数量关系有明显的几何意义或以某种方式将问题转化为几何图形来实现，从而依靠几何图形的特征或性质将问题解决，这就是“数形结合思想”.用数形结合思想来解题的关键在于观察、分析、类比、联想，找出代数问题的几何特征，进而构造出相应的几何模型来解决问题.数形结合能使复杂的代数问题简单化、直观化、形象化，能够提升学生的思维高度，激发学生的学习兴趣.