基于极限状态法的高铁桥上双块式无砟轨道配筋设计研究
2019-10-11胡志鹏
胡志鹏
(中铁第一勘察设计院集团有限公司,西安 710043)
1 概述
至2018年底,我国高铁运营里程已超过2.9万 km,占全球高铁运营总里程的近2/3[1],双块式无砟轨道结构形式是我国主要的无砟轨道结构形式之一,铺设里程长达上万千米。我国现行TB10082—2017《铁路轨道设计规范》主要采用容许应力法,以单一的安全系数笼统考虑结构的安全,虽能满足结构质量安全,但未细化不同分项对结构的影响。极限状态法是采用多系数来取代单一系数,考虑结构构件在施工及使用过程中的各种随机因素,更能切实反映结构构件的实际情况。当前我国建筑、公路、港口、水利水电等行业结构设计规范都采用该设计理论,以结构可靠性理论为基础的考虑多种因素影响的极限状态法应用到结构设计中来,已成为当今世界工程设计界的大趋势[2-9]。
随着铁路运输“走出去”战略的开展,由于轨道结构设计理论不同,致使我国轨道结构设计方法与国外极限状态法的设计标准无法沟通,为了我国铁路技术更好与国际设计方法接轨,2018年中国铁路总公司发布Q/CR9130—2018《铁路轨道设计规范(极限状态法)》[10-12]。本文以此规范为依据,以高速铁路桥上双块式为研究对象,通过与容许应力法做对比,对其道床板及底座进行配筋设计研究[13-20],为后续基于极限状态法的桥上双块式轨道设计提供参考。
2 计算模型及参数
2.1 计算模型
高速铁路桥上CRTSⅠ型双块式无砟轨道由钢轨、WJ-8B扣件、SK-2双块式轨枕、道床板等组成。桥上道床板和底座采用单元分块式结构,道床板宽度和厚度分别为2 800 mm和260 mm,底座板宽度和厚度按2 800 mm和210 mm设计,带限位凹槽,如图1所示。
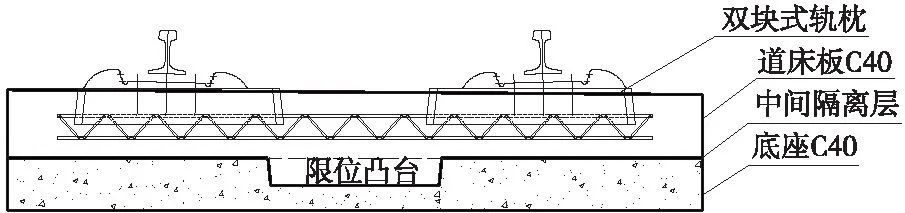
图1 桥上双块式无砟轨道断面
根据桥上双块式无砟轨道结构的特点,结合力学模型,采用有限元软件建立“梁-板-板”模型[2],无砟轨道下部基础施加全约束。钢轨属于细长结构,采用梁单元Beam188模拟,道床板和底座采用板壳单元Shell63模拟,扣件及下部基础采用弹簧单元Combin14模拟,该弹簧单元能够传递垂向压力,但不能传递拉力。为消除边界效应,建立桥上3块道床板的底座进行计算,以中间的道床板和底座作为研究对象,有限元模型如图2所示。

图2 桥梁地段轨道力学模型及“梁-板-板”有限元分析模型
2.2 计算参数
2.2.1 基本参数
桥上CRTSⅠ型双块式无砟轨道扣件节点间距为650 mm,铺设WJ-8扣件,其节点静刚度取为25 kN/mm,动刚度取37.5 kN/mm;道床板和底座采用C40钢筋混凝土。桥梁与底座之间的支承面刚度取为1 000 MPa/m。具体参数见表1。
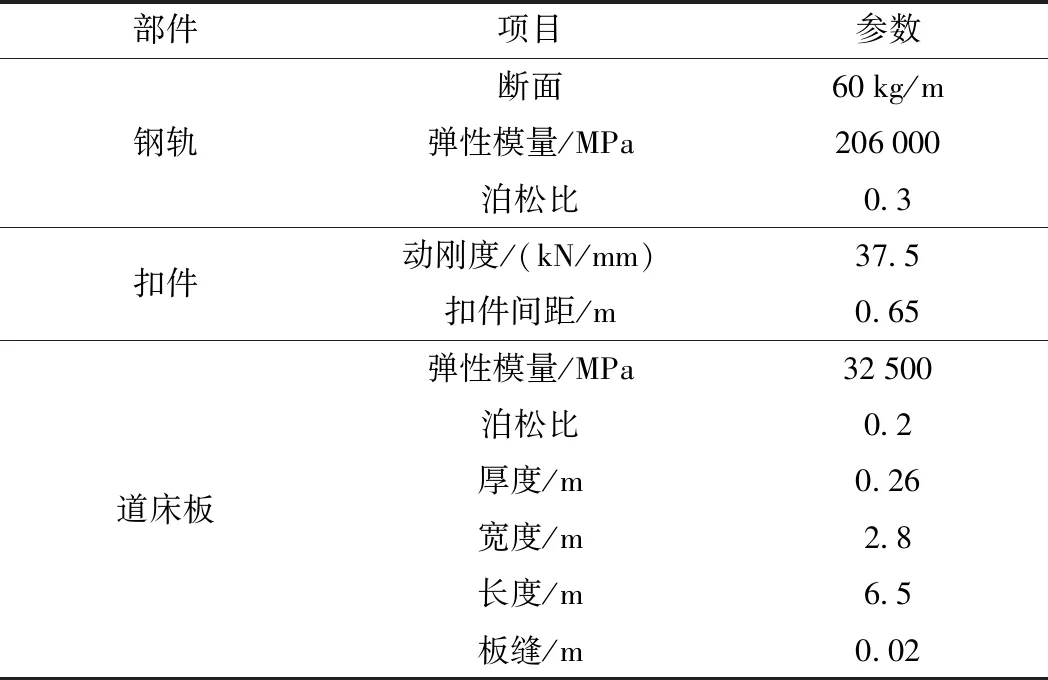
表1 计算参数取值
2.2.2 温度荷载
桥上无砟轨道需考虑温度荷载作用,本文计算最大正温度梯度取90 ℃/m;最大负温度梯度取-45 ℃/m;当温度梯度与其他荷载组合时,取常用温度梯度,即最大温度梯度值的1/2[1]。
2.2.3 桥梁挠曲
桥上双块式无砟轨道配筋设计时应考虑桥梁在列车荷载作用下的挠曲变形,桥梁竖向挠度限值取1/1 600L,桥梁挠曲变形按半波余弦曲线取值。
3 设计荷载
3.1 列车荷载作用
列车荷载采用单轴双轮的加载方式,竖向荷载取值为静轮重的2倍,本文计算采用CRH系列动车组,其设计静轴重为170 kN,列车荷载作用下道床板弯矩结果见表2。
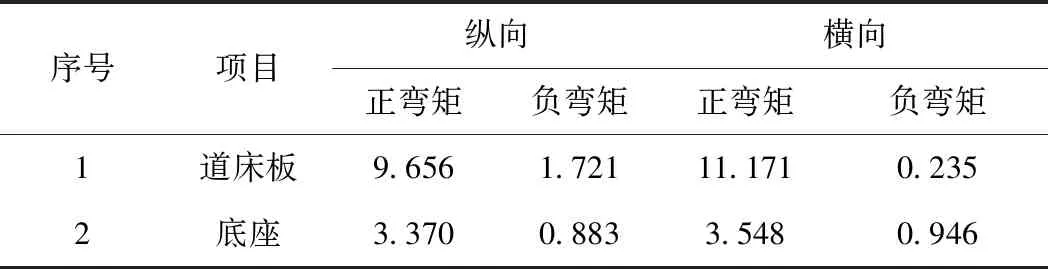
表2 列车荷载作用下道床板弯矩计算结果 kN·m/m
列车荷载作用下道床板的弯矩云图见图3,从计算结果可看出,桥上道床板在列车荷载作用下纵横向正弯矩较大,沿两侧逐渐减小,纵、横向负弯矩较小。
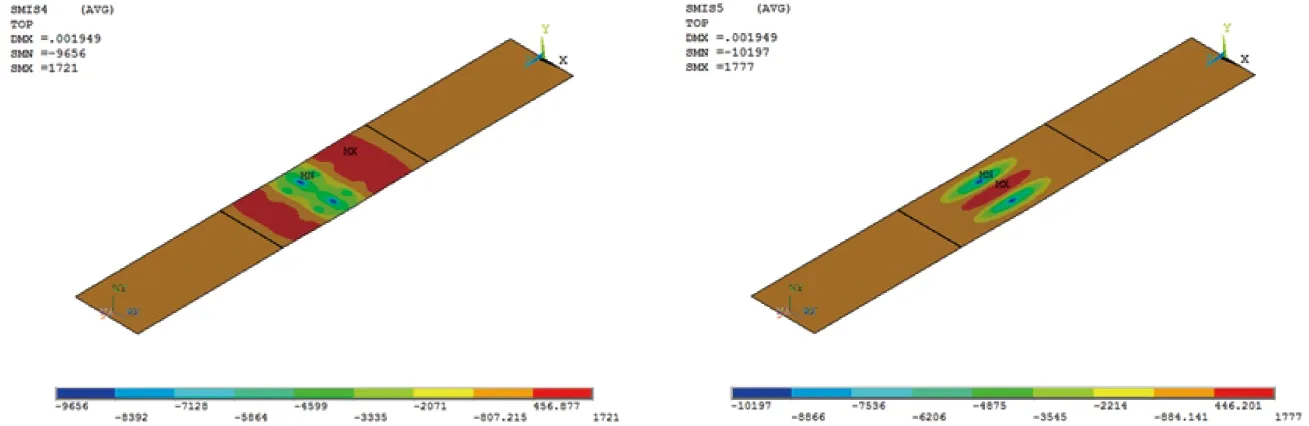
图3 道床板纵横向弯矩云图
3.2 温度梯度作用(表3)
桥上道床板充分暴露在环境中,受环境温度影响较大,主要考虑整体温度升降引起的温度力及温度梯度引起的翘曲应力。底座基本不受温度影响,配筋设计中不考虑温度梯度作用。
式中M——轨道板(或道床板)温度梯度作用弯矩;
W——弯曲截面参数;
Δt——上、下表面温差;
Ec——混凝土的弹性模量;
αt——混凝土的线膨胀系数;
ν——泊松比。

表3 温度梯度作用下道床板纵、横向弯矩计算结果 kN·m/m
3.3 桥梁挠曲作用
桥梁挠曲变形按半波余弦曲线取值,梁端转角取θmax=1/1 000,桥梁挠曲变形作用效应弯矩可按下式进行计算。对于桥梁挠曲变形,仅计其在底面产生的纵向正弯矩。道床板和底座的纵向弯矩如表4所示。
M=EIκ
y=δ(1-cos(πx/L)),
式中 к——下部基础变形曲线的曲率;
δ——桥梁的最大挠度;
L——余弦曲线半周期范围内的长度。
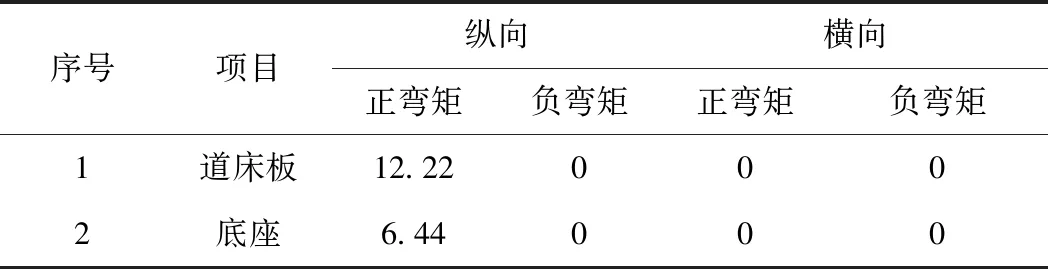
表4 桥梁挠曲变形作用下道床板、底座弯矩计算结果 kN·m/m
3.4 荷载组合
桥上双块式无砟轨道同时受列车荷载、温度梯度及桥梁挠曲变形作用,极限状态法荷载组合中,温度梯度按常用温度梯度考虑。本文桥上无砟轨道结构按极限状态法计算结果配筋设计,但为了与容许应力法的计算结果作对比,同时运用容许应力法计算了道床板和底座的配筋,荷载组合见表5。

表5 不同荷载组合
3.4.1 承载能力极限状态
桥上双块式无砟轨道为单元结构,对于单元轨道结构,承载能力极限状态中荷载组合分为基本组合和偶然组合,荷载效应设计值可取基本组合和偶尔组合中最不利者[10]。
(1)基本组合
M=γdMdK+φtdγtdMtdK+γnqMnqK
式中MdK——列车荷载弯矩标准值,分项系数γd=1.5;
MtdK——温度梯度作用弯矩标准值;
组合系数φtd=0.5;
分项系数γtd=1.0;
MnqK——梁体挠曲变形作用弯矩标准值;
分项系数γnq=1.0;
MR——结构受弯承载弯矩。
(2)偶然组合
单元结构承载能力极限状态偶然组合如下
M=γdMdK+ψtdMtdK
式中,分项系数γd=1.0,ψtd=0.5。
基本组合中考虑了列车荷载、温度梯度及桥梁挠曲作用,而偶然组合中只计列车荷载和温度梯度影响。从上述两种组合中可看出,对于单元结构的道床板,其承载能力极限状态的基本组合起控制作用。
3.4.2 正常使用极限状态
单元结构的正常使用极限状态按标准组合计算荷载效应,考虑列车荷载、温度梯度及桥梁挠曲作用。其结构裂缝宽度需满足按作用的标准组合作用影响计算的裂缝宽度不大于最大裂缝宽度限值。正常使用极限状态标准组合如下式
MQ=φdMdK+φtdMtdK+MnqK
式中,组合系数φd=0.75;φtd=0.5。
3.4.3 荷载组合作用效应
由于承载能力极限状态的基本组合起控制作用,以道床板为例,计算道床板在基本组合作用下弯矩值。同时计算基于容许应力法的道床板弯矩,计算结果见图4及表6。
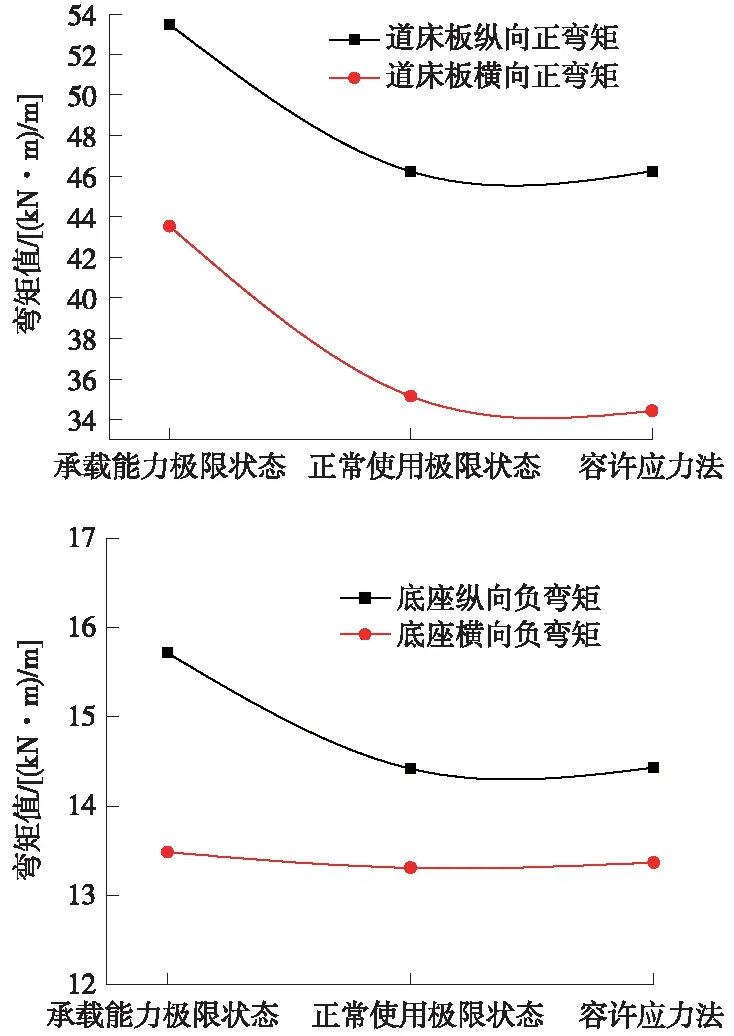
图4 道床板和底座极限状态与容许应力法的弯矩值
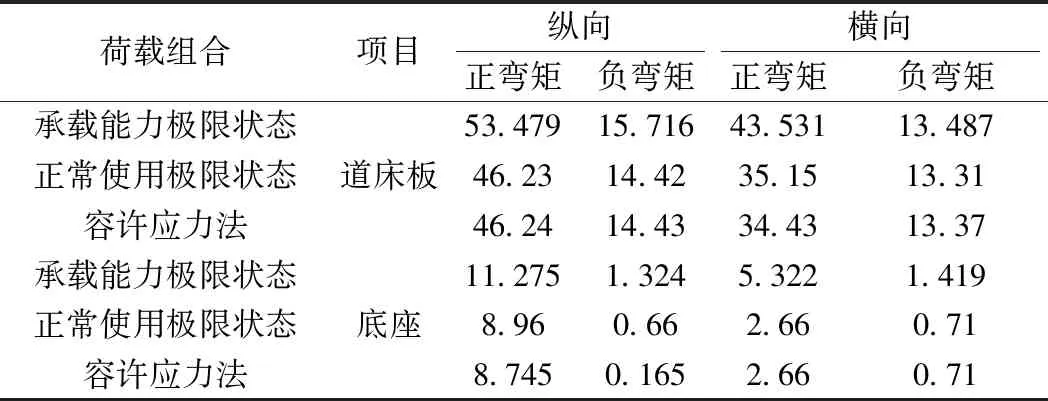
表6 荷载组合作用下道床板及底座弯矩计算结果 kN·m/m
从图4可以看出,承载能力极限状态道床板及底座纵横向弯矩最大,正常使用极限状态与容许应力法计算结果相当。由于承载能力极限状态荷载组合时列车荷载按2倍静轮载计算,且分项系数为1.5,正常使用极限状态分项系数为1.0。容许应力法荷载组合是列车荷载按2倍静轮载计算,且分项系数为1.0。
4 道床板及底座配筋
承载力极限状态配筋设计时基本组合起控制作用,根据混凝土横截面抗弯承载力计算道床及底座配筋,保证配筋结果的抗力弯矩大于承受荷载弯矩。钢筋保护层厚度为30 mm时,室外环境下裂缝宽度容许值为0.2 mm,当保护层厚度变化时,裂缝宽度容许值按0.2(0.3)·c/30进行换算。
式中M——弯矩设计值;
fy——钢筋抗拉强度设计值;
fc——混凝土轴心抗压强度设计值;
As——钢筋截面面积;
ho——截面有效高度;
ξ——相对界限受压区高度;
x——混凝土受压区高度。
正常使用极限状态下结构裂缝宽度检算需满足
w 式中,wlim为最大裂缝宽度限值;w为按作用的标准组合作用影响计算的裂缝宽度,按下式计算 式中K1——钢筋表面形状影响系数,对光钢筋K1=1.0,带肋钢筋K1=0.8; K2——荷载特征影响系数; r——中性轴至受拉边缘的距离与中性轴至受拉钢筋重心的距离之比,对梁和板,可分别采用1.1和1.2; σs——作用组合效应下受拉钢筋重心处的钢筋应力,MPa; Es——钢筋的弹性模量,MPa; d——受拉钢筋直径,mm; μz——受拉钢筋的有效配筋率。 道床板及底座的配筋设计取承载能力极限状态与正常使用极限两者中的较大者,根据弯矩计算结果配置钢筋,同时满足最小配筋率的要求,道床板及底座采用HRB400钢筋,道床及底座配筋如表7所示。 表7 道床及底座配筋计算结果 从表7可以看出,道床板极限状态法纵向比容许应力法计算的纵向配筋少1根φ20 mm钢筋,横向配筋少4根φ16 mm钢筋;底座极限状态法纵向上层比容许应力法少2根φ12 mm钢筋。 采用极限状态法对桥上双块式无砟轨道结构进行配筋设计研究,从不同荷载作用下的弯矩及配筋结果, 得出如下结论:极限状态法中正常使用极限状态计算弯矩结果与容许应力法基本一致,承载能力极限状态计算结果较容许应力大。从道床板和底座的配筋结果来看,桥上双块式无砟轨道单元结构极限状态法的配筋数量略低于容许应力法,节省工程投资。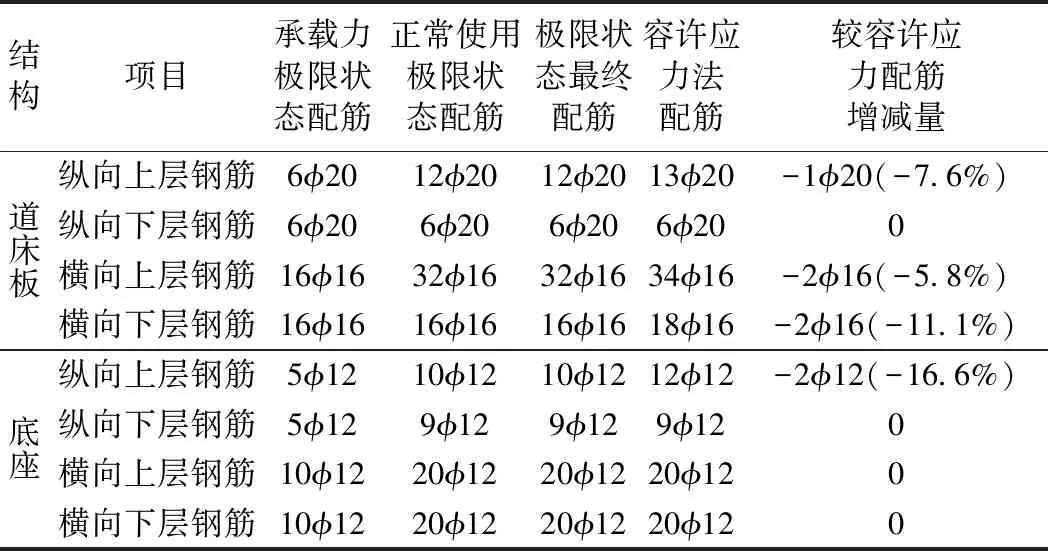
5 结论
