部分边界可穿透的障碍物的正散射问题

彭超权，李傲，郭军

(中南民族大学 数学与统计学学院,武汉 430074)

通常，可穿透障碍物的声波散射问题可以通过Helmholtz方程以及障碍物边界上的传输条件来刻画.但是，在一些实际问题中，障碍物的部分边界可能为理想状态下的薄导体，此时声波会从边界的其余部分透射进入障碍物，这就是本文所要考虑的问题.文献[1]利用线性采样方法重构了散射体，但其中的正散射问题没有给出详细证明.类似的散射问题也出现在电磁波、弹性波散射现象中[2,3].

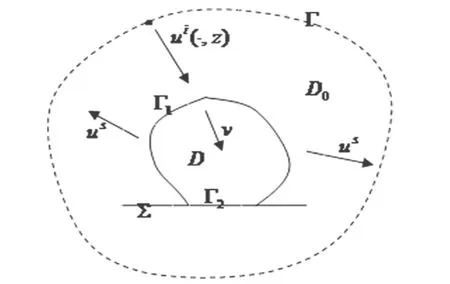
图1 模型简图

1 边界积分方程组

我们考虑如下边值问题：

(1)

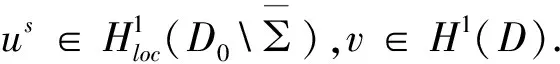
首先证明问题解的存在性.

定理1边值问题(1)最多只有一个解.

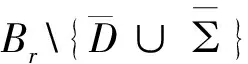
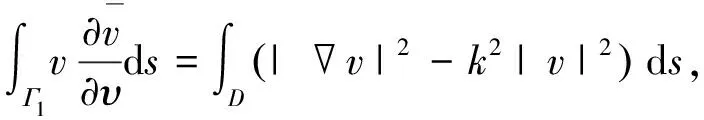
因此我们有：

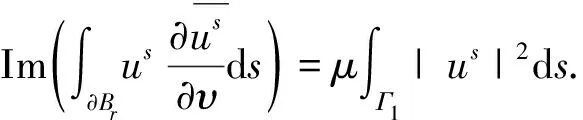
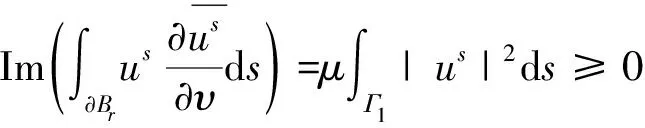
证毕.

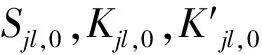
令us，v有如下形式的解：

(2)

(3)

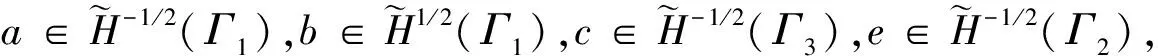
那么在边界Γ1上：

us和v在边界Γ3,Γ2上分别有：

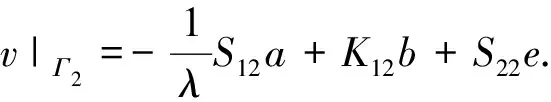
如果定义:

(4)

Aχ=B.

(5)

定义Sobolev空间

以及共轭空间

X*=H1/2(Γ1)×H-1/2(Γ1)×H1/2(Γ3)×H1/2(Γ2),

A显然是从X映射到X*的有界算子.

2 积分方程(5)的解

定理2A是零指数的Fredholm算子.

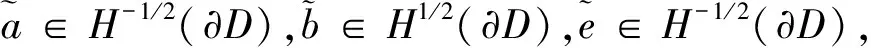
这里j,l=1,2,3.当j=1,2时算子定义在∂D上，当j=3时算子定义在∂Ω上；当l=1,2时，算子在∂D上取值，当l=3时，算子在∂Ω上取值.

由参考文献[7]，存在正下有界算子:

Sl:H-1/2(∂D)→H1/2(∂D),-Tl:H1/2(∂D)→H-1/2(∂D),

使得：

和

并且

是紧算子,其中l=1,2.参考文献[3]第七章.

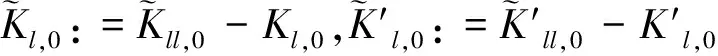
定义：

Y：=H-1/2(∂D)×H1/2(∂D)×H-1/2(∂Ω)×H-1/2(∂D),Y*：=H1/2(∂D)×H-1/2(∂D)×H1/2(∂D)×H1/2(∂D),

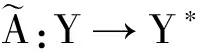
因此有：

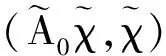
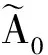
定理3 算子A:X→X*是单射.

证明设χ:=[a,b,c,e]T满足Aχ=0.接下来证明χ=0.

因Aχ=0意味位势满足齐次方程，根据定理2，知

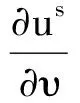
现在重新定义位势us,v形式如(2)和(3)式，但us定义在D上，v定义在D0上.us和v在相应的区域满足Helmholtz方程.利用单双层位势的跳跃关系，在边界Γ1上：

在Γ2上：

根据上面4个式子，得到：

与定理1的证明过程相似，上式只有唯一解，故

因此：

证得a=b=c=e=0，故A是单射.

结合定理1～3，根据Fredholm定理位势算子的性质，问题(1)存在唯一解,且满足：