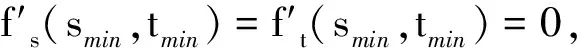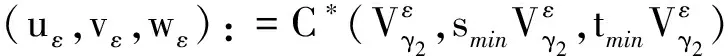含有3个奇异临界方程的椭圆方程组的显式基态解

康东升, 马玉恒, 田丹丹

(中南民族大学 数学与统计学学院,武汉 430074)

1 相关知识

本文主要研究下列奇异临界椭圆方程组:

(1)

其中，u,v,w∈D1,2(N),u,v,w>0,x∈N{0},D1,2(N)是N)关于范数的完备化空间，并且参数满足下列条件:

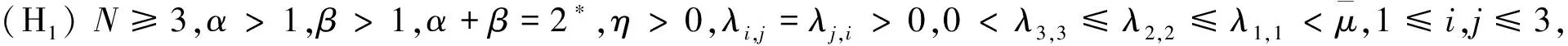
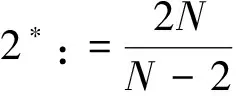
在上述(H1)成立的条件下，矩阵(λi,j)3×3是正定的, 并且对所有的(u,v,w)∈(D1,2(N))3都有同时下列结果成立:

γ1(u2+v2+w2)≤Q(u,v,w)≤γ2(u2+v2+w2),

(2)

其中γ1,γ2分别是矩阵(λi,j)3×3的最小特征值和最大特征值,Q(u,v,w)是一个二次型, 定义如下:

Q(u,v,w):=(u,v,w)(λi,j)3×3(u,v,w)T,∀(u,v,w)∈(D1,2(N))3.

根据Hardy, Sobolev和Young不等式, 我们可以定义如下最佳Sobolev常数[2,3]:

(3)

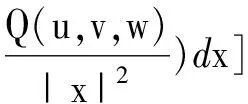
(4)

其中D:=(D1,2(N))3{(0,0,0)},F(u,v,w)我们定义如下:

F(u,v,w):=|u|2*+|v|2*+|w|2*+η|u|α|v|β.

近年来,许多学者研究和讨论了涉及到Hardy不等式的临界椭圆方程(参见文献[2-8])和临界椭圆方程组(参见文献[9-15]),并且取得了很多成果.在文献[3]中,Terracini证明了最佳常数S(μ)的达到函数为:

(5)

其中Uμ(x)是如下径向对称函数:

Uμ(x):=

通过对这些涉及Hardy不等式的临界椭圆方程和方程组的研究,很多重要问题都得到了解决.

对任意的(u,v,w)∈(D1,2(N))3,方程组(1)对应的能量泛函J(u,v,w)如下:

其中J∈C1((D1,2(N))3,),E(u,v,w)定义如下:

(u,v,w)∈(D1,2(N))3是方程组(1)的一个解, 如果(u,v,w)>0,并且满足:

J′(u,v,w),(φ,φ,ψ)=0,∀(φ,φ,ψ)∈(D1,2(N))3,

其中J′(u,v,w)是J在(u,v,w)的Fréchet导数.

(u0,v0,w0)是方程组(1)的一个基态解, 如果(u0,v0,w0)是方程组(1)的一个解,并且在方程组(1)的所有解中取得J的最小能量值,即满足:

J(u0,v0,w0)≤J(u,v,w),

其中(u,v,w)是方程组(1)的任意一个解.

在本文中,主要研究方程组(1)的显式基态解和对应的最佳Sobolev常数的达到函数对.如果在N{0}中有u,v,w>0,则称(u,v,w)是正的.设γ2是矩阵(λi,j)3×3的最大特征值，作如下定义:

(6)

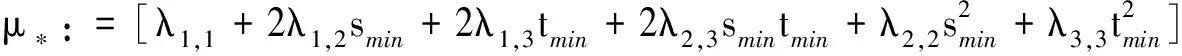
其中(smin,tmin)是函数f(s,t),s,t≥0的最小值点.

本文的主要结果归纳为如下定理.

S*=f(smin,tmin)S(μ*)=f(smin,tmin)S(γ2),

最佳Sobolev常数S*有径向对称并且严格递减的达到函数对,形式如下:

其中有一个函数对是方程组(1)的显式基态解.

在本文中,为了书写方便我们用C来表示常数，有时也会省略积分式中的dx.

2 主要结果的证明

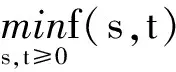
0

对任意的w∈D1,2(N){0},利用函数对(w,sminw,tminw)在(4)式中检验Rayleigh商,可以得到:

S*≤

结合(3)式,可以得到:

S*≤f(smin,tmin)S(μ*).

(7)

设{(un,vn,wn)}⊂D是S*的极小化序列,并且定义zn=snvn,yn=tnwn,其中:

由此可以得到:

(8)

由Young不等式和(8)式,可以得到:

(9)

又由(2),(3),(8)和(9)式可得:

当n→∞时,可以得到:

S*≥f(smin,tmin)S(γ2).

(10)

假设μ*=γ2,由(7)式和(10)式可以得到:

S*=f(smin,tmin)S(γ2),

由此可以得到S*有如下形式的达到函数对:

基态解(uε,vε,wε)对应的极小能量值为:

定理1证明完毕.