线性回归分析模型在股票投资中的应用
2019-10-09车冠贤董婵
车冠贤 董婵
当今股票投资的相关预测已成为经济领域的热门话题。众所周知,股票的价格每分每秒都在变化中,这使股票投资者在进行股票交易时存在很多风险。本文以上证指数的指标作为研究的因变量(最高价、最低价、收盘价、涨幅、跌幅及总手),分别于开盘价进行线性回归分析,然后剔除相关性较小的指标,最终进行多元回归分,对投资者提供一些決策建议。
一、研究背景
中国股市是中国改革开放过程中发展起来的。中国股市即是改革的晴雨表,也是经济的晴雨表,这就是所谓“双重晴雨表”。历史上,中国股票市场的重要节点与经济增长的速度有关,也与体制改革的进程有关。中国股民非理性行为投资。从散户的心理因素角度研究,专家认为心理因素是决定散户交易行为的主要因素,而这是非理性的,其投资行为是建立在虚无缥缈之上,股票的价格决定于投资者心理预期所形成的合力。散户的交易行为受到很多非理性因素的影响,如“羊群行为”、盲目跟风和追涨杀跌等现象。
二、线性回归模型
(一)一元线性回归模型的基本假设
线性回归是存在线性关系的变量,而非线性回归的变量就是非线性。线性回归分析那个就是刻画变量之间的关系模型。
最简单的线性回归模型就是一元的,只有一个变量,定义它的表达式:
这里,Y被称为被解释变量,X称之为解释变量,和是参数,称之为随机干扰项。若是n个样本数据的情况下,(2.1)式也可以化为下式:
回归分析模型可以通过解释变量的值预测被解释变量,为了使得模型更加稳定,需要将参数估计优化。
(二)多元线性回归模型的形式
一般的,对于多元线性回归模型的数学表达式:
这里Y为被解释变量,为回归系数。常数项的参数作为估计值。(2.3)式有时候也可以称为随机表达形式,也称总体回归方程。
其非随机表达式为:
这里的解释变量X对给定时Y的平均值。是偏系数,当其他的变量不变时,Y的均值E(Y)伴随变化而变化,这样的给出的变化对Y的影响。
给定样本数据集,总体回归模型可以写成以下数学表达式:
(三)多元回归方程的估计
对于回归分析,其参数进行估计。对于样本统计量来估计参数,即用估计参数,这样就得到:
其中,是参数的估计值,是因变量y的估计值。
(四)线性关系显著性检验(F检验)
对于Y和k个自变量是否具有相关性,其相关性是否显著,那么就需要对其相关性进行检验。一般有以下几步:
提出假设:
不全为零
原假设成立的条件下,统计量:
由此,在显著性水平,查表得到界,这样就计算出F统计量的数值后,判断(或)来拒绝(或接受)原假设,最终判断原方程的显著性。
三、实证分析
(一)数据来源
本文选取上证指数1990年12月到2017年12月的指标(最高价、最低价、收盘价、涨幅、跌幅及总手)构成样本集,将股票的最高价、最低价、收盘价、涨幅、跌幅及总手作为自变量,第二天的开盘价格作为因变量,建立线性回归模型,从而对股票的开盘价进行了预测。
(二)模型建立
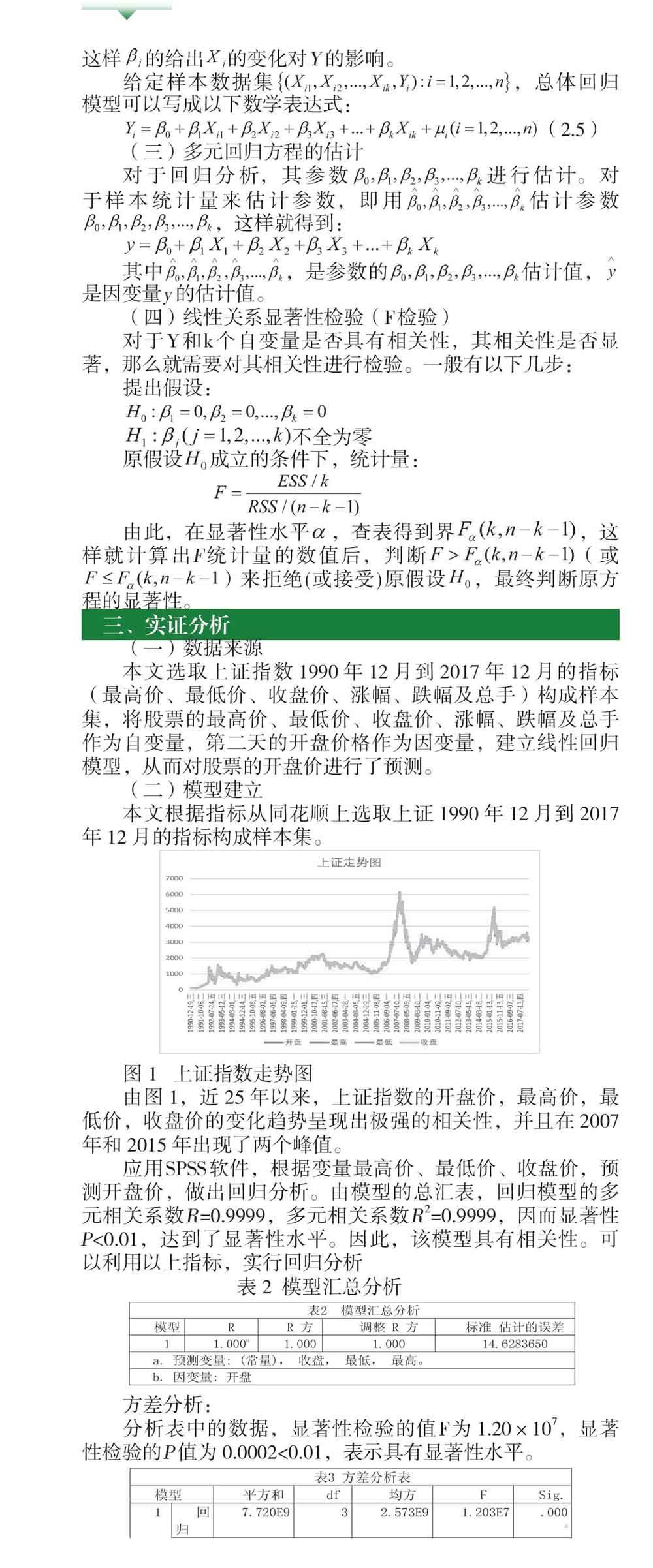
本文根据指标从同花顺上选取上证1990年12月到2017年12月的指标构成样本集。
由图1,近25年以来,上证指数的开盘价,最高价,最低价,收盘价的变化趋势呈现出极强的相关性,并且在2007年和2015年出现了两个峰值。
应用SPSS软件,根据变量最高价、最低价、收盘价,预测开盘价,做出回归分析。由模型的总汇表,回归模型的多元相关系数R=0.9999,多元相关系数R2=0.9999,因而显著性P<0.01,达到了显著性水平。因此,该模型具有相关性。可以利用以上指标,实行回归分析
(三)检验分析
把2018年1月到3月的数据作为检验样本,运用得到的线性回归模型,得到方差表:
因此在误差是P<0.5,模型是可信的。开盘价受到前面最高价,最低价,以及收盘价的影响,其中收盘价影响最大。
四、结语
通过近20年的数据样本,建立回归模型,得到回归方程:Y=-0.785+0.922X1+0.641X2+0.565X3
根据上面的指标表,前一天的收盘价对于第二个交易日的开盘价影响是最大的,因此根据大盘指数,近期交易日的收盘价,最高价,最低价预测开盘价,这样有利于在投资中更加理性决策。
随着居民收入的不断增加,理财投资的意识也逐步提高,但是由于缺乏必要的金融知识,很多人都是在股市上盲目跟风。基于线性回归模型的研究,了解基本的金融逻辑,建立起金融框架。一个理性的决策,直接影响着投资的胜败。股票的投资,必定伴随着风险。在投资之前,充分的认知自己的风险承受能力,要认识股市的高风险性,更加全面认识风险与收益。投资是时间的最好回馈,保持理性,做一个价值投资者而不是投机者。(作者单位:广东石油化工学院理学院)
