双圆弧的图解及其在衣缝轮廓线设计中的应用
2019-10-09娄少红
娄少红
(湖北理工学院 艺术学院, 湖北 黄石 435003)
随着CAD/CAM在造船、航空、汽车、机械等行业中的广泛应用,各类曲线的拟合和逼近显得越来越重要。由于双圆弧的简单直观、实现方便、具有几何不变性以及良好的光顺性,而得到了大家的重视。对此,早期研究者有Bolton[1]、苏步青等[2]、孙家昶等[3]。多年以来,诸多学者对圆弧样条曲线的构造[4]、双圆弧逼近各类曲线的拟合方法、拟合误差及算法[5-7]进行了大量的研究,有的研究者还根据不同行业的实际问题针对双圆弧的应用进行了深入的探讨[8-10]。早在2005年,李重就将双圆弧用于袖窿弧线和袖山弧线的设计[11],但总体上对双圆弧在服装行业的应用研究文献仍较少。为此,本文考虑到可操作性和实用性,基于图解法分析双圆弧,试图通过双圆弧在裤子轮廓线设计中的应用,为破解目前衣缝轮廓线的设计过分依赖版型师经验,且不易参数化的难题,提供切实可行的方法和途径。
1 双圆弧的图解
图1示出双圆弧形态。双圆弧的定义[2,6]为:设2点P1和P2及其切线t1和t2都被给定,引2段圆弧A11和A12,使其满足下列条件:1)A11以P1为起点,且切线为t1;2)A12以P2为止点,且切线为t2;3)A11的终点Q1是A12的起点;4)A11和A12在点Q1处具有共同的切线。则圆弧A11与A12的组合称为双圆弧,点Q1称为双圆弧的连接点(本文简述为连接点)。双圆弧是G1连续的,它有C型和S型2种基本类型[5,12]。
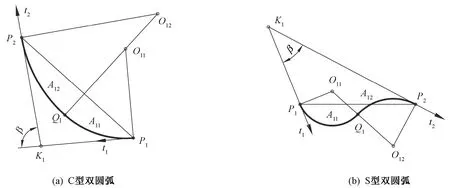
图1 双圆弧Fig.1 Biarc of C-type (a) and S-type (b)
图1中的K1是双圆弧起止点切线t1和t2的交点,K1P1的长度称为起点切线长,K1P2的长度称为止点切线长,t1和t2单位向量之间的夹角β称为切向夹角,其取值范围为(0°,180°)。
可以知道平面上的圆弧唯一地决定于3个条件,从而双圆弧共有6个自由度,但在双圆弧的定义中只有5个自由度,所以还有1个未确定的自由度,这表明连接点的位置并不唯一确定[2,5-6]。因此,平面上任意2点P1和P2之间,存在无数条首尾分别经过这2点,且首尾端(起止点)的切线分别为t1和t2的双圆弧,这些双圆弧形成一个双圆弧族[9],其连接点的位置按照一定规律变化而形成一条轨迹线。实际上,连接点的轨迹并非一致连续而存在间断点。所谓间断点,简单地说是指该点并非连接点。间断点将连接点的轨迹线分割成多个区间,且不同区间对应不同类型和不同组成的双圆弧。
显而易见,双圆弧的连接点轨迹、类型和组成,取决于双圆弧起止点切线t1和t2的交点位置以及方向关系。
1.1 起止点切线的交点位于起止点连线外
双圆弧起止点切线t1和t2的交点K1位于起止点连线P1P2之外时,起点切线长K1P1与止点切线长K1P2的大小关系有K1P1
1.1.1 起止点切线t1和t2的方向相顺
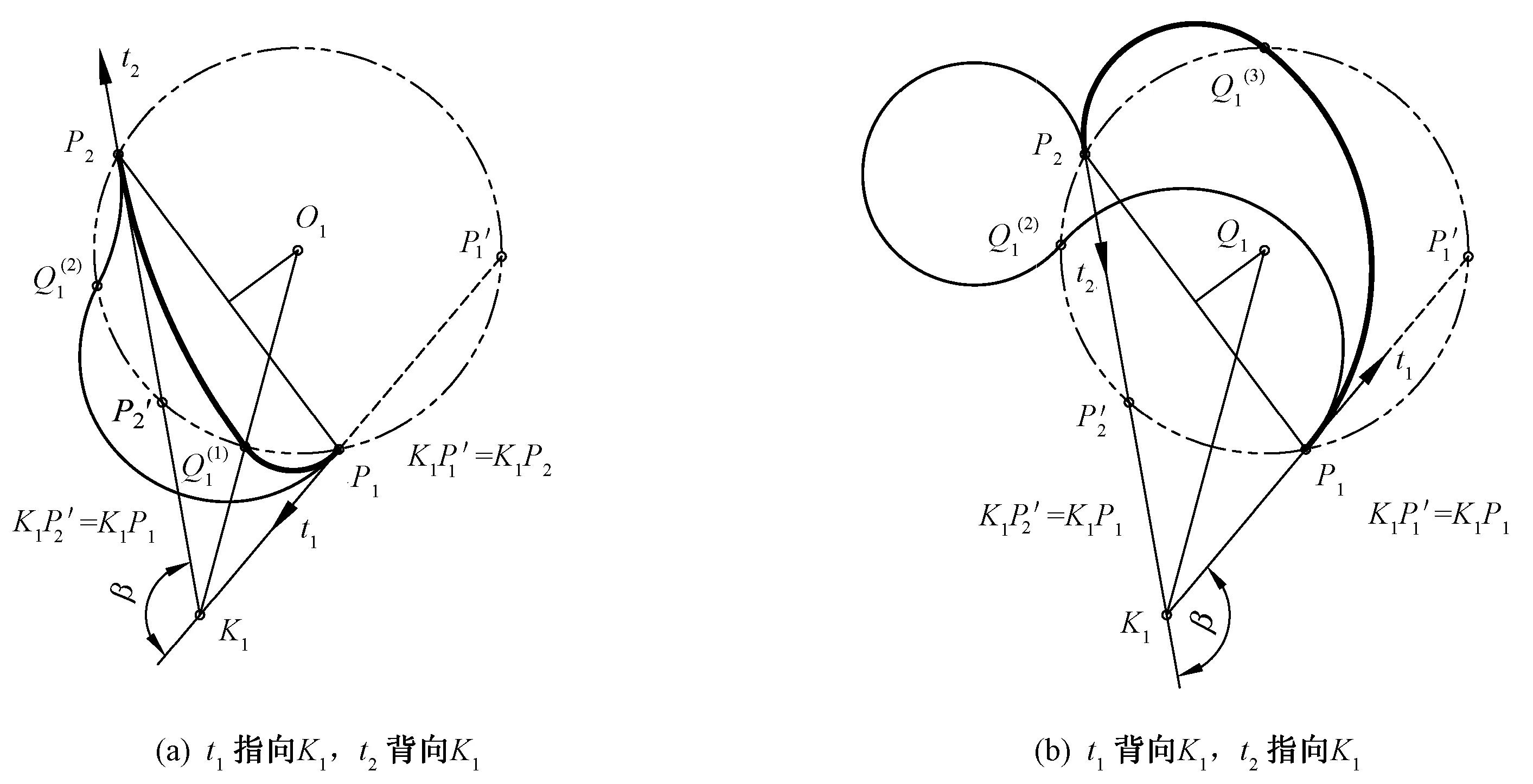
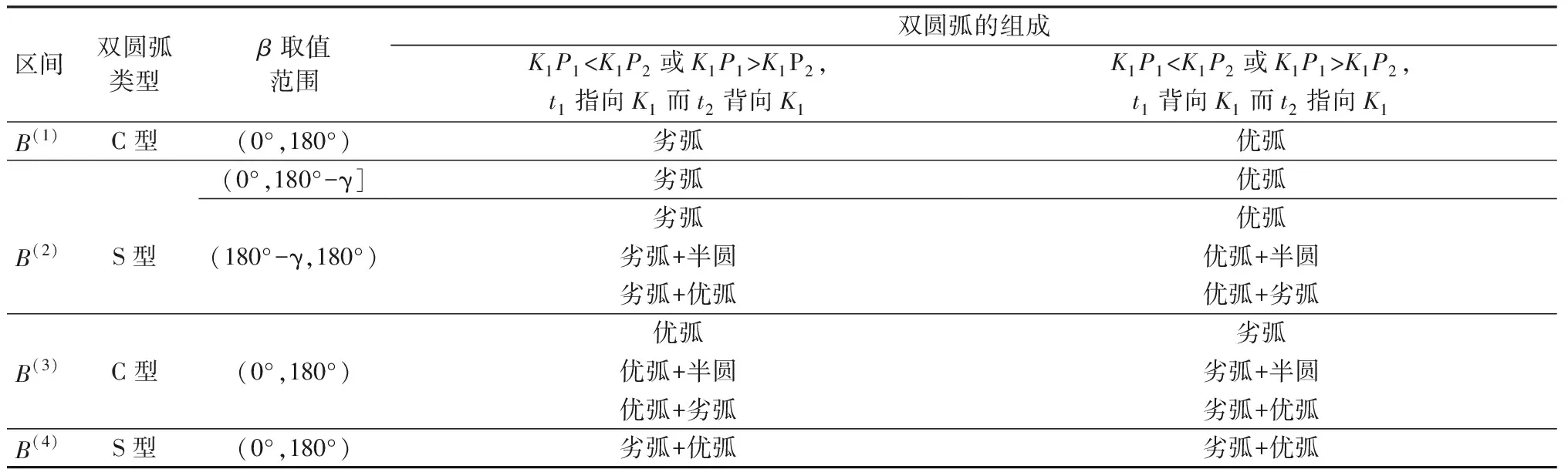
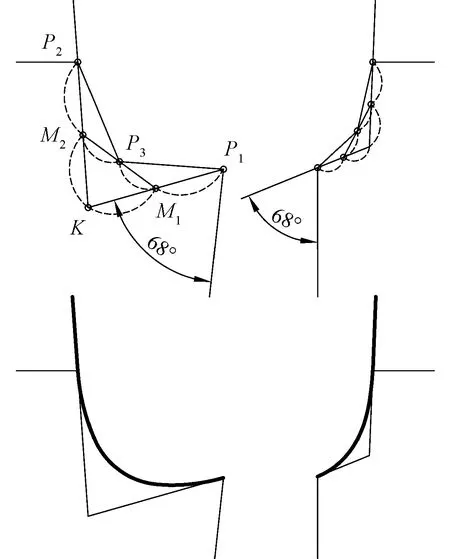
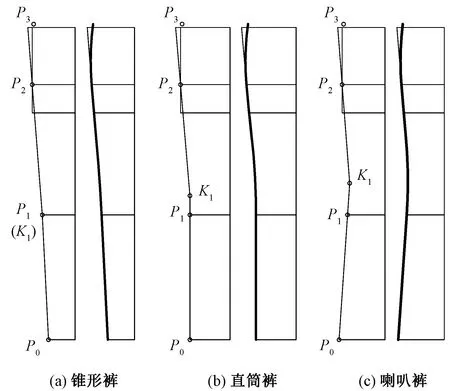
设K1P1 2)连接点轨迹圆的圆心与半径。作∠P1K1P2(β的补角)的角平分线与连线P1P2的垂直平分线相交,其交点O1即为连接点轨迹圆的圆心。连线O1P1(或O1P2、O1P1′及O1P2′)的长度,即为连接点轨迹圆的半径。其它求圆心O1的方法,从略。 3)连接点轨迹圆的间断点及区间。显然,双圆弧起止点P1和P2不是连接点。由于过点P1′或P2′只能作出一段圆弧与一段直线相切,所以P1′、P2′也不是连接点。因此,连接点轨迹圆上共有P1、P2′、P2和P1′等4个间断点,它们将其分成(P1,P2′)、(P2′,P2)、(P2,P1′)和(P1′,P1)这4个区间。 图2 K1位于连线P1 P2之外且t1和t2方向相顺Fig.2 K1 is located outside P1P2 and direction of t1 and t2 is consistent. (a) t1 Points to K1, t2 is backward K1; (b) t1 is backward K1, t2 points to K1 同理可解K1P1>K1P2且t1和t2的方向相顺(图略)时的情形。 对于连接点轨迹圆的区间,为推而广之,规定以△P1K1P2为参照,将位于△P1K1P2之内(或以起止点P1和P2为端点)的区间记为B(1),较长切线段之外的区间记为B(2),较短切线段(或者其延长线)之外的区间记为B(4),余下的区间记为B(3)。按此规定,上述区间(P1,P2′)、(P2′,P2)、(P2,P1′)和(P1′,P1)则可依次记为B(1)、B(2)、B(3)、B(4)。 4)各区间双圆弧的类型及组成。当K1P1 表1 双圆弧类型及组成(K1位于连线P1 P2之外且t1和t2方向相顺)Tab.1 Type and composition of biarc(K1 is located outside P1P2 direction of t1 and t2 is consistent) 1.1.2 起止点切线t1和t2的方向相背或相对 同理可解K1P1>K1P2且t1和t2的方向相背或相对(图略)时的情形。 当K1P1 双圆弧起止点切线t1和t2的交点K1无论是与起点P1重合(起点切线长K1P1=0),还是与止点P2重合(止点切线长K1P2=0),t1和t2的方向关系均有相顺、相背等2种情形,其连接点的轨迹均为一个圆,如图4所示。 1.2.1 起止点切线t1和t2的方向相顺(重点重合) 如图4(a)所示,当双圆弧起止点切线t1和t2的交点K1与起点P1重合(K1P1=0)且t1和t2的方向相顺(此时t1背向K1,而t2指向K1)时,按前述方法可求得连接点轨迹圆的圆心和半径;在起点P1的切线t1上,取P1P1′=P1P2截取P1′点,则点P1′即为连接点轨迹圆上的间断点。间断点P1(K1)、P2和P1′将连接点轨迹圆分成(P1,P2)、(P2,P1′) 和(P1′,P1)这3个区间,规定以起止点为端点的区间记为E(1),不以重合点为端点的区间记为E(2),余下的区间记为E(3)。 图3 K1位于连线P1 P2之外且t1和t2方向相背或相对Fig.3 K1 is located outside P1P2,and t1 and t2 are back to back (a) or face to face (b) 区间双圆弧类型β 取值范围双圆弧的组成K1P1 图4 K1与P1重合且t1与t2相顺或相背Fig.4 K1 and P1 coincide and t1 and t2 direction is consistent (a) or back to back (b) 同理可解K1P2=0且t1和t2的方向相顺(图略)时的情形。 当K1与P1重合(K1P1=0)或K1与P2(K1P2=0)且t1和t2的方向相顺时,连接点轨迹圆上不同区间的双圆弧类型及组成如表3所示。 1.2.2 起止点切线t1和t2的方向相背(交点重合) 当双圆弧起止点切线t1和t2的交点K1与起点P1重合(K1P1=0)且t1和t2的方向相背(如图4(b)所示),或者K1与止点P2重合(K1P2=0)且t1和t2的方向也相背(图略)时,连接点轨迹圆的圆心与半径、间断点及区间的求解方法同上,不再赘述。连接点轨迹圆上不同区间的双圆弧类型及组成如表3所示。 表3 双圆弧类型及组成(K1与P1或P2重合)Tab.3 Type and composition of biarc(K1 in coincidence with P1 or P2) 双圆弧起止点切线t1和t2的交点K1在无穷远处(起止点切线相互平行)时,起止点切线的方向关系有t1与t2同向平行、反向平行2种情形,见图5。 图5 起止点的切线平行Fig.5 Tangential parallel of starting and ending points. (a) t1 is parallel to t2 in same direction; (b) t1 is reversely parallel to t2 1.3.1 起止点切线t1与t2同向平行 1.3.2 起止点切线t1与t2反向平行 表5 双圆弧类型及组成(t1与t2反向平行)Tab.5 Type and composition of biarc(t1 and t2 are reversely parallel) 2.1.1 C型双圆弧的基本构造条件 纵观前述,C型双圆弧有2种构造情形符合由劣弧组成的要求,即 1)表1中,β的取值范围为(0°,180°),t1与t2方向相顺,且t1指向K1,连接点位于区间B(1)内的C型双圆弧。 2)表5中,α的取值范围为(0°,180°),且t1与t2反向平行,连接点位于区间(P1′,P2)内的C型双圆弧。 一般而言,只有前一种构造情形适用于设计衣缝轮廓线,因此,本文后续提及的C型双圆弧专指前一种构造情形。 2.1.2 C型双圆弧的切线长比值要求 考虑到可操作性,本文采用限定切线长比值大小的方法控制C型双圆弧的圆顺性。 切线长比值大小的限定值与切向夹角β相关。在切向夹角β的取值范围(0°,180°)内,切线长比值与切向夹角β的关系必须符合 在满足上述要求时,切线长比值越小,C型双圆弧的圆顺性越好。 2.1.3 C型双圆弧连接点的选择 连接点的位置有无限多个,如何选择合适的连接点将直接影响到双圆弧的圆顺性。一般采用使2段圆弧曲率之差最小的原则来确定连接点的位置[5-6,12]。 本文在保证双圆弧圆顺性的前提下,顾及手工制图的可行性,以图2(a)所示区间(P1,P2′)内的连接点轨迹弧的中点,即△P1K1P2的内心为C型双圆弧的连接点[2,7]。 2.1.4 C型双圆弧的制图要点 绘制C型双圆弧的方法有内心法和圆心法。 1)内心法。内心法是指制图时先确定双圆弧连接点的方法。内心法适宜用AutoCAD制图,便于参数化计算,但用于手工制图时稍显复杂。 如图1(a)所示,用AutoCAD制图的基本步骤是先调用XLINE命令作△P1K1P2的内心Q1,再用PLINE命令画出C型双圆弧。 2)圆心法。圆心法是指绘图时先确定2个组成圆弧圆心的方法。圆心法比较适合手工制图。 圆心法的基本步骤是先求圆弧A11和A12的圆心和半径,尔后画弧,如图6所示。求作圆心和半径的过程可归纳为:一条连线,两个相等,一条垂直平分线,两条法线。 图6 绘制C型双圆弧的圆心法Fig.6 Center method for drawing C-type biarc 2.2.1 S型双圆弧的基本构造条件 纵观前述,S型双圆弧有如下几种构造情形符合由劣弧组成的要求,即 1)表1中,β的取值范围为(0°, 180°-γ],t1与t2方向相顺,且t1指向K1,连接点位于B(2)区间内的S型双圆弧。 2)表2中,β的取值范围为(0°,γ],K1P1 3)表3中,β的取值范围为(0°,90°],K1P1=0且t1与t2方向相背和K1P2=0且t1与t2方向相顺,连接点位于E(1)区间内的S型双圆弧。 4)表4中,α的取值范围为(0°,90°),且t1与t2同向平行,连接点位于区间(P1,P2)内的S型双圆弧。 在上述S型双圆弧的多种构造情形中,用于衣缝轮廓线设计的通常有3种,即t1与t2相交(K1P1 图7 S型双圆弧常用的3种构造情形Fig.7 Three kinds of construction situations commonly used for S-type biarc. (a) Intersected and direction consistent; (b) Intersected and direction back to back; (c) Coincide and direction back to back 2.2.2 S型双圆弧的切线长比值要求 图7(a)所示S型双圆弧构造情形的切线长比值必须大于等于3,图7(b)和图7(c)所示的构造情形没有切线长比值要求。 2.2.3 S型双圆弧连接点的选择 S型双圆弧连接点的选择,除须满足圆顺性要求外,还要顾及可操作性。为此,本文采用定弦长的方法选定连接点,经分析和实践,依据衣缝轮廓线的形状特征,选定连接点Q1与双圆弧起点或止点的距离为Q1P1(或Q1P2)=(0.4~0.5)P1P2,如图7所示。 2.2.4 S型双圆弧的制图要点 S型双圆弧用手工制图时较复杂,但适宜用AutoCAD制图。 用AutoCAD制图的一般过程如下:首先画出连接点轨迹弧:图7(a)所示作图方法是在确定点P2′后,用三点画弧ARC命令过P1、P2′、P2画出连接点轨迹弧;图7(b)所示作图方法是在确定点P2′后,再经过P2′、P1、P2画连接点轨迹弧;图7(c)所示作图方法是先确定切向夹角β的角平分线lβ,再以lβ为切线(实际上lβ就是连接点轨迹圆在P1点的切线),用起点、端点和方向画弧命令画出连接点轨迹弧。尔后依据衣缝轮廓线形状选定双圆弧的连接点,最后使用PLINE命令画出S型双圆弧。 S型双圆弧的3种构造情形,看似很复杂,实际上,根据拓扑学的理论,可以认为这3种情形是等价(同胚)的,即图7(c)是图7(a)的一种特殊情形,而图7(b)可以看成是图7(a)某个时刻的状态,因此,在对S型双圆弧参数化时,完全可按图7(a)进行参数计算。 采用双圆弧设计衣缝轮廓线,必须遵循以下准则:无论在什么数据下,其制图方法完全统一,简单可行,可顾及手工制图需求;其形状符合要求,圆顺合理,无需后期人为干预。 裤子前、后裆缝线均由直线和曲线2部分构成,其曲线部分的形状,受前、后裆宽和前、后裆斜线倾斜度以及前、后裆内侧缝线倾斜度等因素的影响而发生变化,尤其是后裆缝线的曲线部分,由于后裆斜线(臀围线以下段)和落裆线的长度尺寸以及相互间的夹角变化显著,导致其形状起伏很大,难以掌控。对此,本文根据前、后裆缝线曲线部分的形状特征及尺寸变化情况,遵循衣缝轮廓线的设计准则,按照切线长比值要求,将前、后裆缝线的曲线部分均分解成2段相切的C型双圆弧。 图8示出阔腿裤前、后裆缝线曲线部分的制图过程。对后裆缝线的曲线部分,首先使用中位线中点法,在△P1KP2中确定前、后段2段C型双圆弧的公切线M1M2及公切点P3,尔后以P1与P3为起止点、落裆线P1K和线段P3M1为切线、△P1M1P3的内心为连接点;以P3与P2为起止点、线段P3M2和后裆斜线P2K为切线、△P3M2P2的内心为连接点,依次画出2段C型双圆弧,即得裤子后裆缝线的曲线部分。同理可得阔腿裤前裆缝线的曲线部分,以及任何数据下裤子前、后裆缝的曲线部分。 图8 阔腿裤的前、后裆缝线Fig.8 Front and back trouser crotch seam of wide leg trousers 需要说明的是,上述方法是基于降低制图繁琐程度的考量而提出的,实际上若用4段双圆弧设计前、后裆缝线的曲线部分,可以获得更加完美的圆顺效果。 裤子后外侧缝线由直线和曲线2部分构成,影响其曲线部分形状的直接因素,是其直线部分的倾斜度、后外侧缝斜线的倾斜度以及后外侧缝撇入量。由于直线部分的倾斜度受裤子廓形的影响,后外侧缝斜线的倾斜度受裤子松紧风格、后挺缝偏移量等因素的影响,致使后外侧缝斜线与后外侧缝线直线部分之间的夹角以及交点的位置发生很大的变化,加之腰臀差对后外侧缝撇入量的影响,从而导致后外侧缝线形状的显著起伏,似无规律可循,难以把握。对此,本文根据裤子后外侧缝线的形状特征及尺寸变化情况,将其曲线部分解析成1段S型双圆弧和1段单圆弧。 依据上述分析可以认为,裤子后外侧缝线是由直线段(P0P1段)、S型双圆弧段(P1P2段)和单圆弧段(P2P3段)等3段依次相切连接而成的,其中S型双圆弧的起止点分别为P1、P2点,起止点的切线分别为P0P1和P2K1;单圆弧的起点和端点分别为P2和P3。单圆弧与S型双圆弧的公切点为P2,公切线为P2K1,如图9所示。 图9 锥形裤、直筒裤和喇叭裤的后外侧缝线Fig.9 Back outseam line of tapered trousers(a), straight-legged trousers (b) and bell-bottom trousers (c) 如果使用AutoCAD制图,就可以用PLINE命令,一气呵成地画出后外侧缝线。 通过双圆弧在裤子轮廓线设计中的应用可知,只要能根据衣缝轮廓线的形状特征以及相关尺寸的变化情况,将其分解成含有双圆弧的N段,并合理选择双圆弧的类型、起止点和切线以及连接点位置,就可获得完美的衣缝轮廓线。 采用双圆弧设计衣缝轮廓线,不仅能突破经验的束缚,提高衣缝轮廓线设计的合理性和科学性,还可以破解衣缝轮廓线的参数化难题,简化服装样板的参数化设计,大幅度降低计算难度和计算量,使更多的服装从业者能够采用AutoCAD参数化功能进行样板的参数化设计,提高制图速度,从而提升生产效率。 FZXB
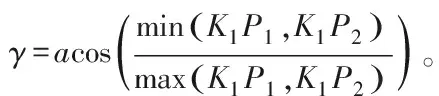

1.2 起止点切线的交点与起点或止点重合
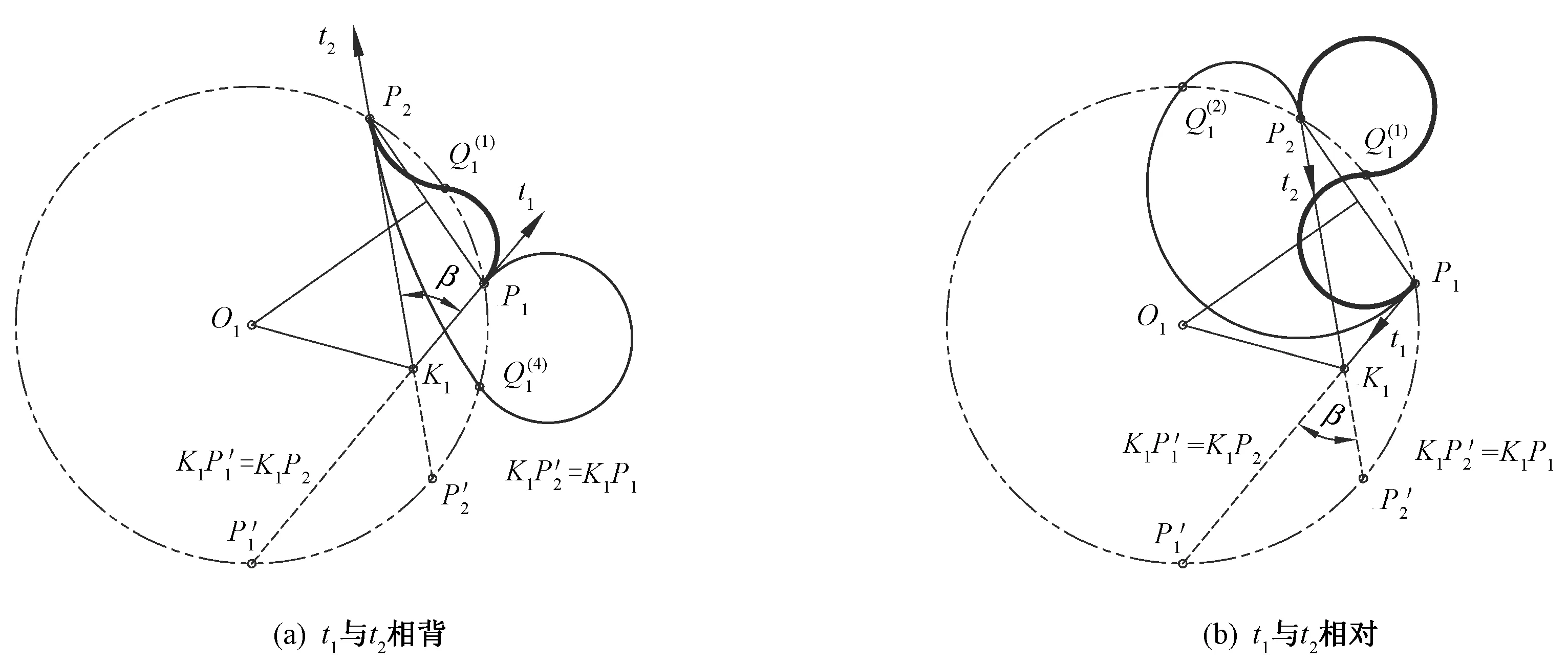
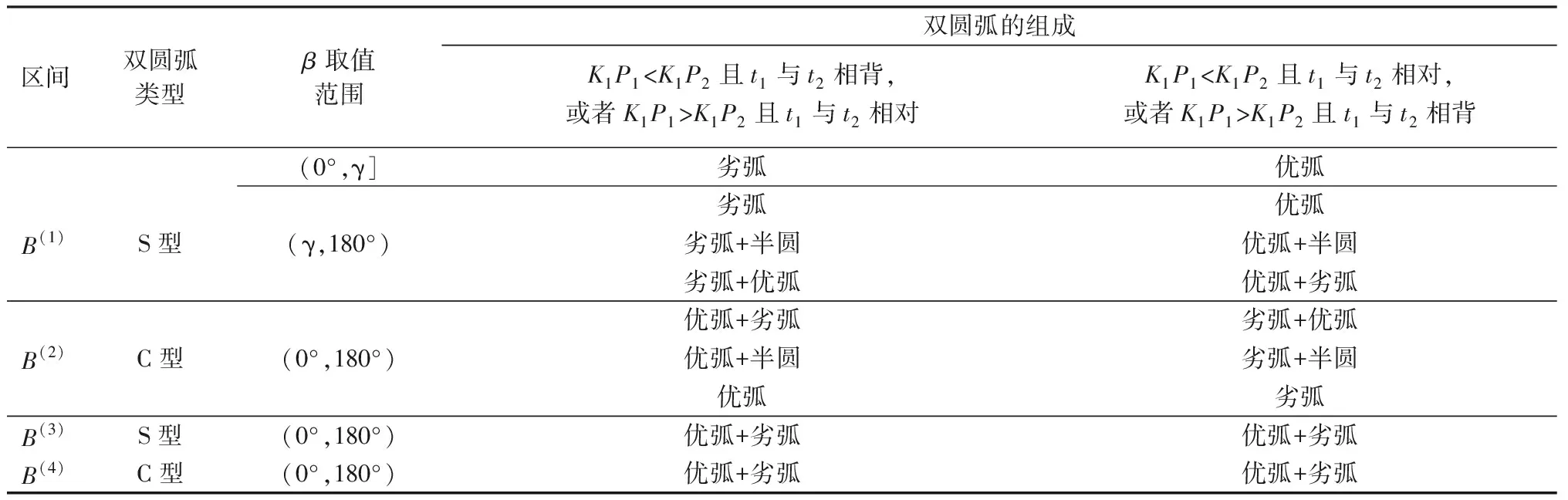

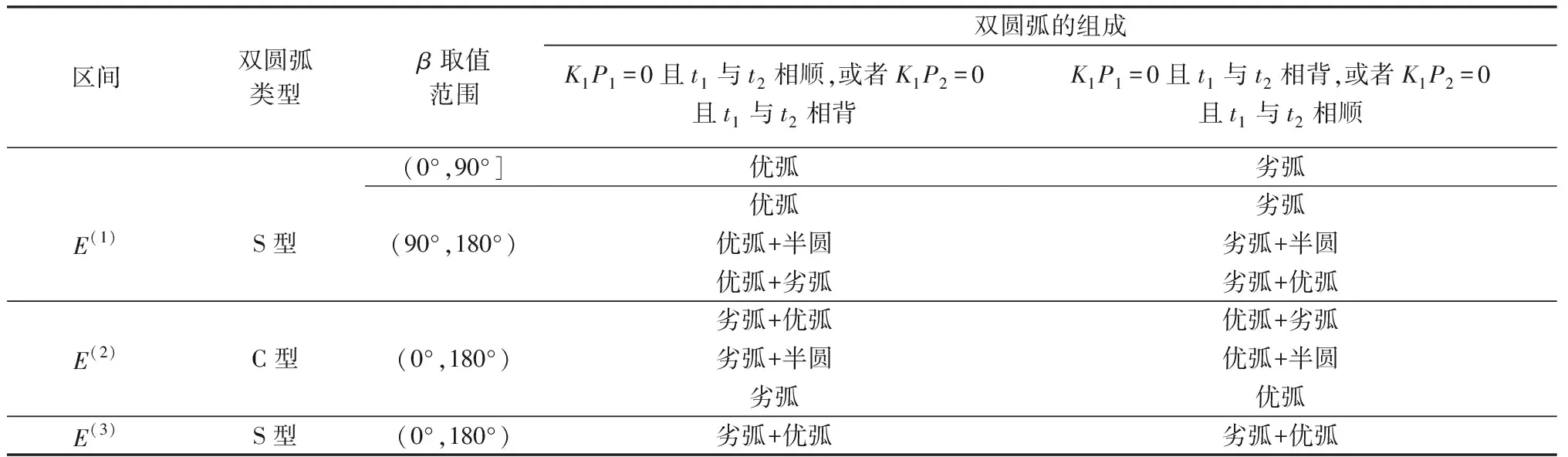
1.3 起止点的切线交点在无穷远处

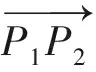
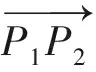
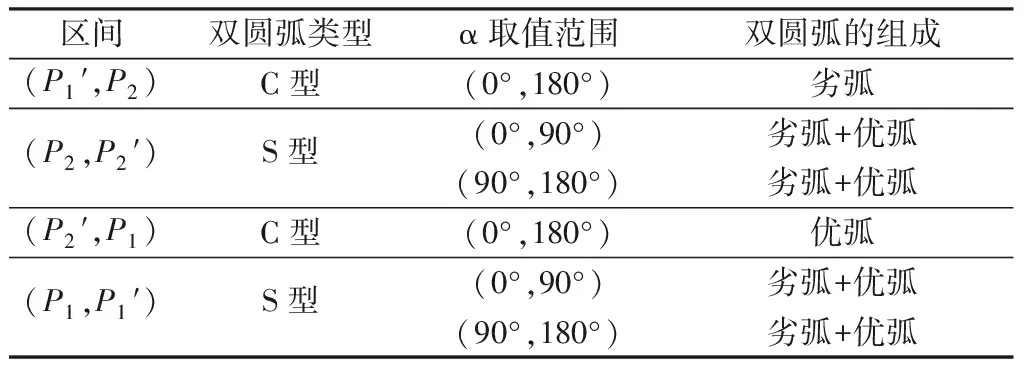
2 用于衣缝轮廓线设计的双圆弧

2.1 C型双圆弧
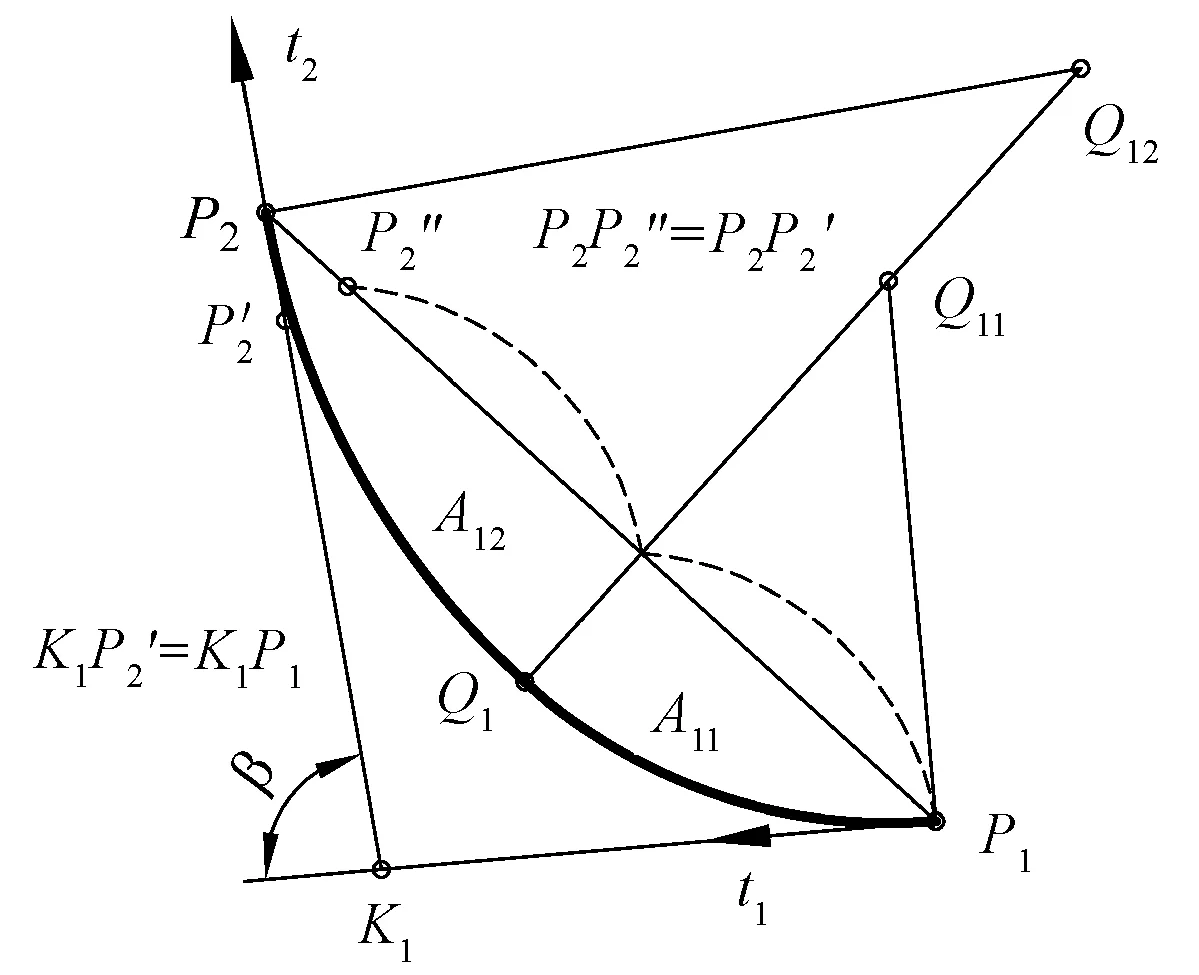
2.2 S型双圆弧
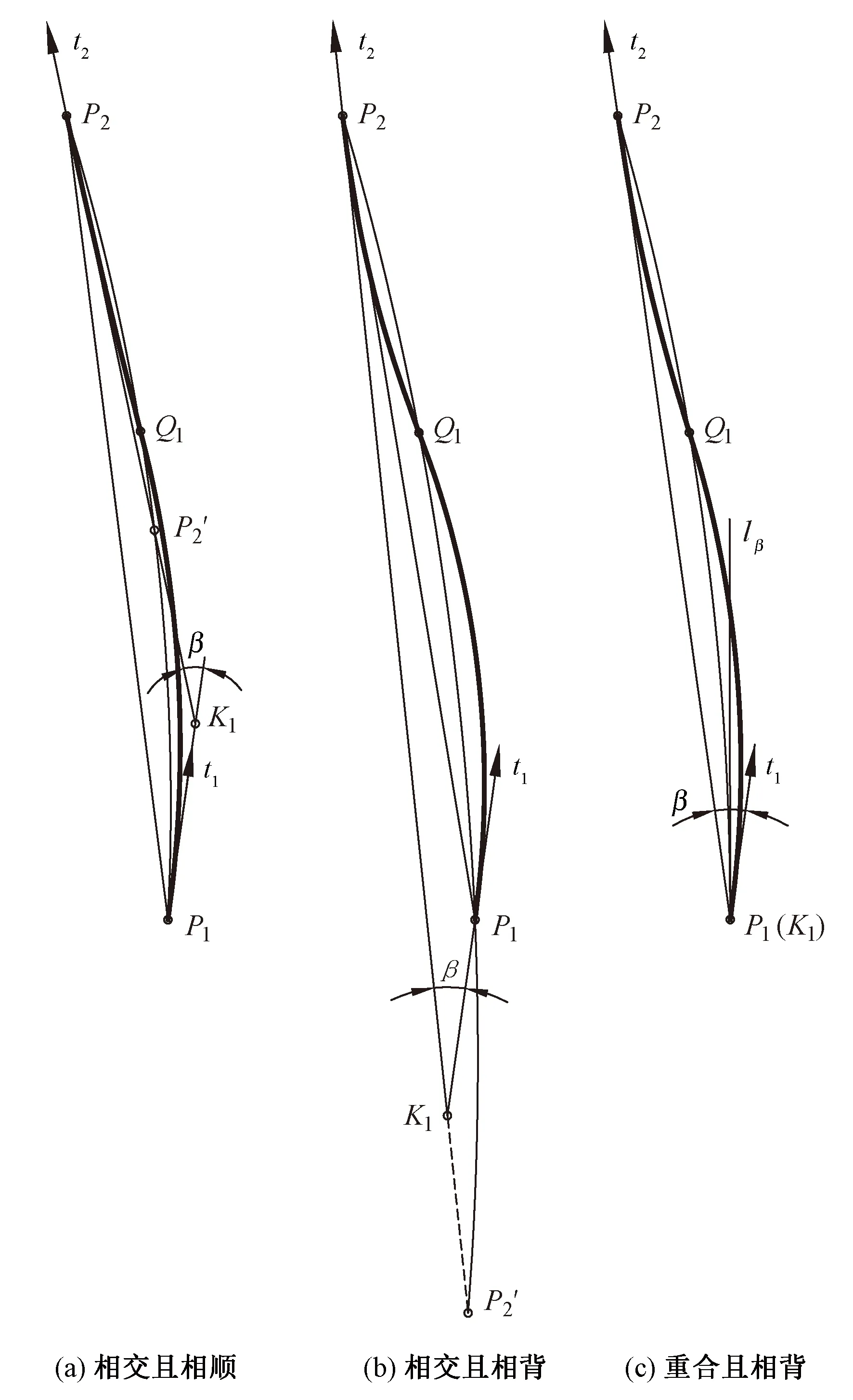
3 双圆弧应用实例
3.1 双圆弧在裤裆缝线设计中的应用
3.2 双圆弧在裤子后外侧缝线设计中的应用
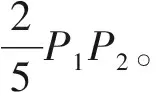
4 结 论
