解析高中数学教学中培养学生逻辑思维能力的策略
2019-10-09江苏省泰州市民兴实验中学申天渠
江苏省泰州市民兴实验中学 申天渠
逻辑思维能力是正确、合理思考的能力,为在授课中培养这一能力,做好教材知识讲解,储备丰富的数学知识是基础。同时,结合教学实践,灵活应用多种教学方法,有针对性地进行引导、训练,最终将知识升华为能力。
一、抽象能力的培养
众所周知,高中数学很多知识由生活中的问题抽象而来。抽象是运用数学知识解答实际问题的基础,也是推动数学发展的关键能力。培养抽象能力不仅对现有知识的学习、理解有所帮助,而且对以后的终身发展大有裨益。为更好地提升抽象能力,一方面深入讲解数学基础,使学生深入理解数学符号代表的含义,尤其针对数学公式应引导其探求本源,做到不仅会应用,更要会推导。另一方面,立足数学教学内容,讲解相关例题,做好示范,使学生认真体会抽象过程,能够将相关情境与数学知识建立联系,进而顺利求解。
例1:使用0 和1 分别替代杨辉三角中的偶数与奇数,得出如图1 所示的图形,请认真观察,分析第n次全行均为1 的是第___行;第61 行中1 的个数为:____。

图1
分析:该题目要求结合给出的情境解答问题,显然,要想解答出该题目,需要找到其中的规律,将给出的情境抽象为数学符号。观察可知:第1 次全行为1 的行为第1 行;第2 次全行为1 的行为第3行;第3 次全行都为1 的行为第7 行……由此可见,第n次全行均为1 的是第(2n-1)行。则不难推出第26-1=63 行都为1,从而逆推出第61 行中1 的个数共有32 个。
二、转化能力的培养
高中数学试题复杂多变,部分试题直接作答难度较大,不仅抽象难懂,而且过程烦琐。事实上,如在准确把握题干的基础上加以巧妙的转化,问题便迎刃而解。为使每位学生都能掌握这一技能,则需要做好转化能力的培养。一方面结合教学内容,讲解转化方法,包括换元法、构造法、坐标法等。针对每一种方法,结合具体例题,讲解具体应用。另一方面,转化对知识储备、知识应用灵活程度要求较高,需进行长久训练,因此,可优选经典试题,通过开展专题训练、各个击破等教学活动,提供给学生更多机会,促进学生转化能力的提升。
例2:已知函数f(x)=ax+cosx,x∈[0, ],若满足f(x)≤1+sinx,则a的取值范围为_____。
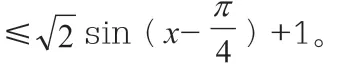
三、推理能力的培养
推理是一种基于事实或条件,结合自身经验、知识,推导出正确结论的能力。推理能力是学习数学的重要思维能力之一,关系着学习成绩的提升。一方面,传授推理经验。推理不是主观臆断,每一步结论的得出都应有理有据。同时,注重推理前后的连贯性,思维缜密,经得起推敲。另一方面,提供推理机会,积极创设推理情境,提供更多锻炼的机会,活跃课堂的同时,充分调动推理的积极性,使学生尝到推理的成就感,树立推理的自信心,更加热爱数学知识的学习。
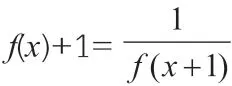
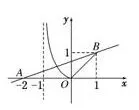
图2
分析:题干给出x∈[0,1]时函数f(x)的表达式以及f(x)和f(x+1)的关系。知道在区间(-1,1]内,g(x)=f(x)-mx-2m有两个零点,因此,需要根据已知条件进行推理,求出在区间(-1,1]内f(x)的表达式。具体推理过程如下:
∵x∈[0,1]时,f(x)=x,
当-1 <x<0 时,0 <x+1 <1,∴f(x+1)=x+1。
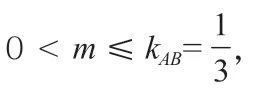
四、结论
逻辑思维能力是一个较为抽象的概念,理论上讲凡是动脑的活动,都可归为逻辑思维能力范畴。逻辑思维能力是学习高中数学的重要能力,教学中引起足够重视,认真实践相关的培养工作。本文通过探讨得出以下结论:
其一,高中数学涉及的逻辑思维较多,为更好地完成培养任务,需做好理论学习与研究,结合授课知识,有目的、有计划地开展培养工作,以获得事半功倍的良好效果。
其二,做好培养工作研究,针对不同逻辑思维能力的培养工作,应做好培养策略总结,尤其不断创新,大胆实践,不断提高逻辑思维能力培养水平。
