立足课堂,培养数学核心素养
——以《勾股定理》教学设计为例
2019-10-09江苏省苏州工业园区星港学校
江苏省苏州工业园区星港学校 陈 芳
随着时代的进步和课程改革的推进,培养学生的核心素养日益成为教育教学中的重点。其中数学学科核心素养包括数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析六个方面,在平时的教学中我们要注重培养学生的这些数学素养,让其感受数学文化,体味数学魅力,会用数学的眼光观察、思考现实世界。本文以“勾股定理”为例,旨在探究如何在初中数学教学中落实数学核心素养。
一、创设问题情境,感受数学文化
数学作为一门既抽象又与生活息息相关的学科,有着悠久灿烂的文化,在教学中我们既要增强学生对知识的理解和应用,也要引领学生在具体情境中感受数学的博大精深,领略人类的智慧进步。为此在《勾股定理》这一课的一开始我就介绍了2002 年国际数学家大会在北京举行,并重点展示了它的会标——弦图,它标志着我国古代数学的重要成就。这个图形里到底蕴涵了怎样博大精深的知识呢?以此激发学生的好奇心,引出课题,并简单介绍勾股定理的历史,促使学生感受数学文化,激发爱国热忱。
二、渗透思想方法,拓宽数学思维
数学思想是数学的灵魂,在教学中,既要重视知识形成的过程,更要渗透其在产生、形成与发展过程中所蕴藏的思想方法,进而拓宽学生的数学思维。
在探索勾股定理的过程中,根据学生已有的生活经验,由特殊到一般设计了三个活动:
1.等腰直角三角形ABC两直角边和斜边之间有什么关系呢?
(1)如图1,方格图每个小方格的边长为1,分别以等腰直角三角形ABC的三边向外画正方形,它们的面积S1、S2、S3有何关系?
易得S1=S2=1,S3=2,从而S1+S2=S3,进而得在Rt △ABC中,AC2+BC2=AB2。
(2)如图2,方格图中分别以腰长为3 的等腰直角三角形ABC的三边向外画正方形,它们的面积S1、S2、S3有何关系?
易得S1=S2=9,关键点是如何求S3。在学生思考、讨论的基础上归纳出求图形面积常用的两种方法:“割”“补”,分别如图2(a)、2(b),进而求得S3= 18,所以S1+S2=S3,可得在Rt △ABC中,AC2+BC2=AB2。
2.做一做:如图3,方格图中分别以直角边为2、3 的Rt △ABC的三边向外画正方形,它们的面积S1、S2、S3有何关系?Rt △ABC的三边有何关系?
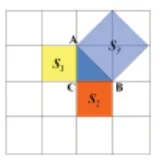
图1

图2
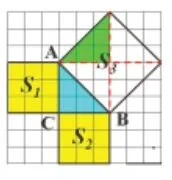
图2(a)
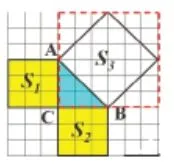
图2(b)
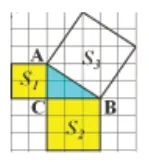
图3

图4
3.探究普通的直角三角形的三边关系:如图4,弦图是由四个全等的直角三角形拼成的正方形,易证中间是个小正方形,设直角三角形的三边分别是a、b、c,如何表示小正方形的面积?学生易得小正方形的面积有两种表示方法:①S小正方形=(b-a)2,②S小正方形=c2-4×0.5ab,从而可得等式(b-a)2=c2-4×ab,整理得a2+b2=c2,即得勾股定理。
在整个探索活动中渗透了由特殊到一般、数形结合等重要数学思想,用“割补”法求图形面积的方法,促使学生体验到数学活动充满了探索性和创造性,感受证明的必要性以及结论的确定性,最终完成由感性认识到理性认识的升华。
三、引导思考练习,加强概念理解
在教学中,得出概念、定理后,需通过适当的练习来加强对概念的理解,进而掌握基础知识、基本技能,为后续应用作准备。
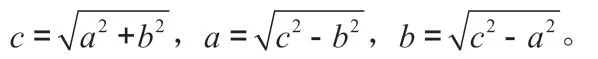
1.如图5,在Rt △ABC中, ∠C= 90°。
(1)若a=12,b=5,则c=_____;
(2)若a=6,c=10,则b=_____;
(3)若a= ,b= ,则c=____;
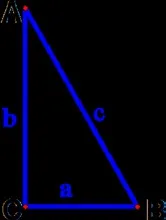
图5
2.判断题:
(1)直角三角形三边分别为a,b,c,则一定满足下面的式子:a²+b²=c²。
(2)直角三角形的两边长分别是3 和4,则第三边长是5。
第一类练习题的设计目的是会用勾股定理求直角三角形中第三边,并训练数学运算能力;第二类练习题的设计目的是让学生明确利用勾股定理的前提条件是直角三角形,并且利用勾股定理时一定要分清楚直角边、斜边。
四、解决实际问题,体味数学魅力
数学源于生活,用于生活,教学中在注重学生基本知识与技能掌握的同时,应设计一些生活中的实际问题,使学生体验从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程,从而体味数学魅力。
在本节课的最后一个环节实际应用中,由浅入深地抛出两个实际问题:
1.消防员救火问题:某楼房三楼失火,消防队员赶来救火,了解到每层楼高2.6 米,消防队员取来5.41 米长的云梯,如果梯子的底部离墙基的距离是2.16 米,则消防队员能否进入三楼灭火?
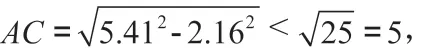
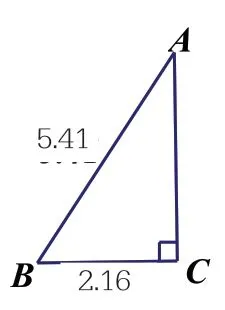
图6
最终在探讨、合作中,学生进一步加深了对勾股定理的理解,并体验了估算法的应用。
2.印度数学家婆什迦罗曾提出的“荷花问题”:平平湖水清可鉴, 面上半尺生红莲; 出泥不染亭亭立,忽被强风吹一边。渔人观看忙向前,花离原位二尺远;能算诸君请解题,湖水如何知深浅?
解本题的关键是引导学生读懂题目,画出图形,将实际问题转化为数学问题:
已知:如图7,AD=0.5 尺,AC=2 尺,∠CAB=90º,BD=BC,求AB的长。
图中有Rt △ABC,但只知直角边AC的长,所以无法直接用勾股定理。考虑到BC=BD=AB+0.5,可设未知数,列方程来求解:设AB=x,则BC=x+0.5,在Rt △ABC中,AB2+AC2=BC2,故可得x2+22=(x+0.5)2,进而求得AB的长。
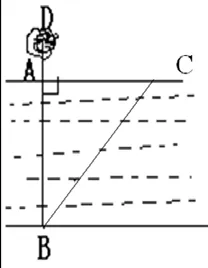
图7
在这两个实际问题的解决中,积累了学生的活动经验,提高了学生解决现实问题的能力,同时也培养了学生的问题意识、应用意识。
总之,在注重学生核心素养培养的大背景下,我们的教学设计要在考虑学生学情、数学认知规律、心理特征的基础上,创设问题情境,激发学习兴趣,引发独立思考、主动探索、合作交流,使其理解和掌握数学基础知识、基本技能、基本思想方法、基本活动经验,体验从实际背景中抽象出数学问题、构建数学模型、寻求结果、解决问题的过程,进而感悟数学的价值。
