数感的“生态”教学尝试
——以《二次根式的加减》教学为例
2019-10-09南京师大附中新城初级中学黄山路分校
南京师大附中新城初级中学黄山路分校 张 洁
在《二次根式的加减》教学过程中,联想到2016 年刘乃志特级教师在镇江的一节展示课,课上使用了面积为8 和18 的两个正方形引入二次根试的加减法问题,当时笔者想如果刘老师止步于列出加式,对于大部分同学们能不能靠自己的感觉,成功地化简两个二次根式并发现二次根式合并的方法呢?通过教学实践,发现大部分学力较优的同学是可以做到的,那这节课我们该如何上才能让大部分孩子有所收获呢?对此,笔者在课堂上进行了相应实践。尝试如下:
一、教学过程
1.数感在尝试中“孕育”
活动1 如图1,由低到高的三个正方形的面积分别是2,8 和18,试计算三个正方形的边长之和。
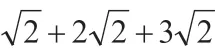
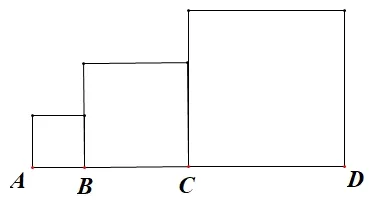
图1
2.数感在思辨中“生根”
问题1 请试着再举几组通过加减运算可以合并的二次根式,要进行二次根式加减运算,它们具备什么特征才能进行运算?
设计意图:通过同学们举例,说明依据这样的特征举例的,从每一组具体的可以合并的二次根式中归纳出怎样的二次根式可以合并,即同类二次根式的概念。借助多次追问,能启发学生主动反思自己的学习过程,积极探寻知识的内核。
想一想:在下列二次根式中是同类二次根式的有哪些?
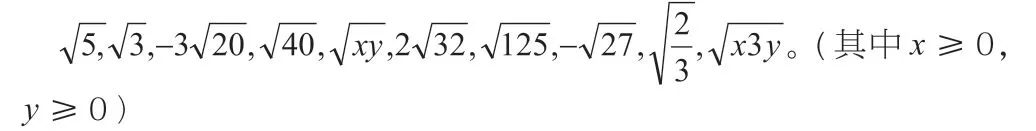
设计意图:通过找同类二次根式,进一步明确同类二次根式的特征。本处设计了两个带有字母的同类二次根式,为下面带有字母的二次根式的加减运算作铺垫。
设计意图:再次让同学们尝试计算,进一步类比合并同类项,在计算过程中梳理二次根式加减法的运算步骤。
问题2 通过刚才的计算,你能试着说出怎样进行二次根式加减吗?
设计意图:学生通过运算,总结运算过程中发现的二次根式的加法法则。
3.数感在应用中“发芽”
例1 计算:
设计意图:三道计算各具代表性,通过本组训练题,进一步巩固和深化同类二次根式的概念,运用二次根式相加减的法则进行化简和计算,进一步形成运算能力,提升数学素养,加强交流,让思想充分碰撞,促进生生的共同发展。
例2 如图2,两个圆的圆心相同,半径分别为R、r,面积分别是27 cm2、3 cm2。求圆环的宽度(两圆半径之差)。
设计意图:在解决实际问题过程中,感受二次根式加减法的必要性。
拓展提高:当a取什么值时,二次根式和是同类二次根式?
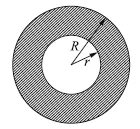
图2
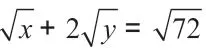
4.数感在反思中“成长”
引导学生本节课中的定义、法则和方法三个角度回顾反思。
二、教学反思
1.何时形成同类二次根式的概念
同类二次根式是进行二次根式加减运算过程中的“产物”,是在二次根式加减过程中,为了判断“什么样的二次根式可以通过加减合并”得到同类二次根式,没有此概念也不影响“二次根式加减法”知识体系的形成。因此将同类二次根式概念放在新课开始较为突兀,可以让学生独立尝试计算时,让同学们感知需要引入一个名词来描述 “化简后,被开方数相同” 的二次根式,再引入同类二次根式概念,水到渠成。
2.在情境问题中是直接凭“意识”计算,还是列式后戛然而止
通过教学实践,对于大部分同学都可以通过联系二次根式的化简,独立尝试,得到运算结果,剩下的也可以通过教师引导得到结果,只不过计算过程中“意识”占了主导,教师没有必要打破他们合理的“感觉”,重建概念。可以顺势而为,理清计算依据,反思计算方法,构建运算法则。这样过程体现了运用数字和运算法则进行灵活运算的能力,同时也体验培养其积极的学习态度与信心。这样的概念形成过程也是数感“生根”的过程。
3.基于数感的教学必要性
《数学课程标准》明确地把数感作为数学学习的内容之一提出来,要求初中生“建立初步的数感和符号感”。简单而言,数感是我们对数字关系和数字模式的意识,以及运用这种意识灵活地解决数字问题的能力,学生具有“数感”的典型特征就是他们能够对其所面对的数字模式、数字关系和计算过程进行归纳,并能够把新知识和已有知识联系起来。
教学中不妨将学生学习中已产生的这种意识,应用于新知的学习。像有理数的运算律引入,解一元一次不等式等,根据学生的经验和感悟,完全可以得到相应的结论,在此基础上对结果的形成过程进行追问和反思,也是建立和运用数感的重要过程。通过一次次“追问”,一次次地“思考”,学生的数感亦在初获结论时“孕育”,在思辨结论时“生根”,在应用结论时“发芽”,在反思结论中“成长”。
