浅析函数性质研究中的一种“天平结构”

江苏省淮阴师范学院附属中学 韩立云

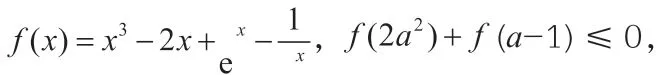
一、研究结构，训练思维

以天平结构为载体，深入研究解法，优化思维，容易形成深刻认识，提升思维能力。

例题1：（苏教版课本原题）已知函数y=f(x)是定义在R上的减函数，f(a+1)＞f(2a)，求a的取值范围。

解法：本题利用单调性很容易得到a+1 ＜2a，得到a＞1。

例题2：已知函数f(x)=x2-2x+a，若f(m)＜f(3)，求m的取值范围。

解法1（代入法）：代入解析式，再解不等式容易求解；解法2（水平线法）：天平结构的本质是比较大小，而y=f(3)这条“水平线”就凸显了其核心地位，与f(3)的大小数量关系就转化成与y=f(3)这条“水平线”图像的上方下方关系，容易得到-1 ＜m＜3。

从上面两个基础例题中不难发现天平结构的三种解法：代入法、单调性、水平线。其中，从思维训练角度“单调性和水平线”为重点方法。基于以上方法分析，再去处理以下问题，便能思路开阔，容易解决。

（2）已知函数f(x)=x2-|x|，若f(m-1)＜f(2)，求实数m的取值范围。

分析：很明显，上面都是“天平结构”，通过结构考查函数性质的研究。基于上面的方法分析，前面3 题应该去画图，通过图像去探寻“单调性”或“水平线”的解决办法，而题（4）只能是研究单调性，进而定性观察分析函数奇偶性和单调性就顺理成章了。

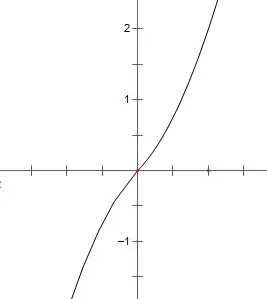
题（1）

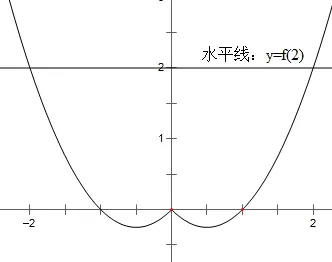
题（2）

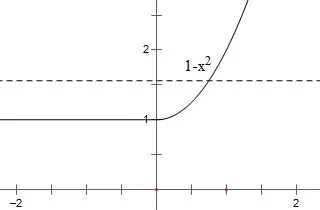
题（3）

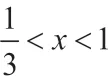
二、联想结构，提升素养

有了“天平结构”的认知以及基本题型的方法研究，就形成了“结构认识”。对于较为复杂的一些问题，通过新题目中个别点与已有结构的相似性就可以产生联想，与已有结构产生直观想象，提升了数学核心素养，激发转化为标准结构，再依据已有研究方法高效解决问题。如：

（6）已知函数f(x)=x3+x+1)，若对于任意的x，都有f(x2+a)+f(ax)＞2，求实数a的取值范围。

分析：两题有着“天平结构”的相似性，进而努力实现转化。题（5）画图发现在定义域上单调递增，发现f（3）=12，从而转化为f(x2-x+1)＜f（3），由图像可得函数在R上单调递增，于是x2-x+1＜3，解得-1 ＜x＜2。题（6）构造F（x）=f（x）-1，则有F（x）=x3+x，F（x2+a）+F（ax）＞0，因为F（x）为R上递增的奇函数，所以有x2+a）＞-ax，容易解得0 ＜a＜4。“天平结构”对题（5）（6）解题过程起到了指向作用，引导转化的方向，大大提高了解决新问题的能力，在结构相似性的联想和直观想象过程中提升了数学核心素养。

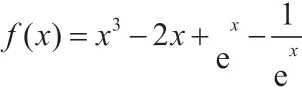
通过上面论述，能看出“天平结构”研究函数性质是有一定作用的，而这种结构化的研究对很多问题解决是有帮助的。对已有内容产生认识，实践中通过结构化再认识，再实践时感受就不一样了，函数性质得到深度掌握，相关能力及素养无形中也提升了。