核心素养视域下的共点力动态平衡问题探析

吕艳坤

(深圳实验学校,广东 深圳 518055)

物体的平衡是力学体系的基础和核心知识,动态平衡是指物体受力状态发生缓慢变化,可视为发生一系列受力平衡的动态过程;此类问题要求在事物的动态变化中洞察、分析、抽象概括、逻辑推理,进而解决问题,[1]由于能够充分考查物理观念和科学思维,一直是高考和自主招生考试的热点.本文对共点力动态平衡问题涉及的题型和解法进行归纳总结,从物理学科核心素养的视角对题型进行立意分析,从而指导教学实践,有效促进学生物理概念、规律的内化和模型建构、科学推理等能力的提高.

1 矢量图解法

矢量图解法是通过力的动态平行四边形或矢量三角形,根据图形的边长和角度动态变化直观地判断力的变化情况.常见的矢量图解法主要有极限法、矢量三角形法和辅助圆法.

1.1 极限法

适用条件:物体受到3个共点力的作用,其中一个力为恒力,另外两个力的大小都单调变化.[2]

解题策略:对物体进行受力分析,采用极限思想,根据物体在动态变化过程中始、末状态矢量三角形的变化,确定力的变化情况.

图1

例1.如图1所示,均匀小球放在光滑竖直墙和光滑的斜木板之间,模板上端用水平细绳固定,下端进而绕O点转动,在放长细线使板转至水平的过程中

(A) 小球对木板的压力逐渐增大.

(B) 小球对木板的压力逐渐减小.

(C) 小球对墙的压力逐渐增大.

(D) 小球对墙的压力逐渐减小.

图2

解析:如图2所示对小球进行受力分析,初始位置木板支持力N大于重力G;采用极限思想,当木板运动到水平位置时,木板支持力N等于重力,墙面支持力F变为0.由牛顿第三定律可知,小球对木板的压力逐渐较小,小球对墙面的支持力也逐渐减小,故选(B)、(D).

1.2 矢量三角形法

适用条件:物体受到3个共点力的作用,其中一个力为恒力,一个变力的方向不变.

解题策略:对物体进行受力分析,依据某一自变量的变化,在同一图中画出动态变化过程中若干状态下的矢量三角形,根据矢量三角形的动态变化确定力的变化情况.

例2.如图3所示,重力为G的球放在倾角为α的光滑斜面上,试分析挡板与斜面间的倾角β为多大时,挡板所受压力最小?

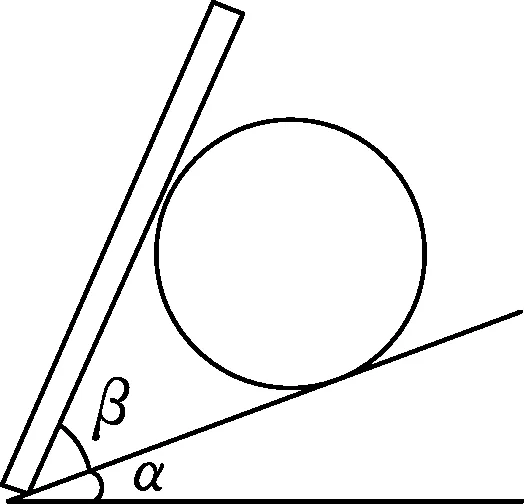
图3

图4

解析:如图4所示，已知重力G的大小方向不变,斜面对球的支持力F1方向不变,根据力的动态矢量三角形可知,当F2垂直于F1时挡板对小球的压力最小;由牛顿第三定律可知当β=90°时挡板所受压力最小.

1.3 辅助圆法

适用条件:物体受到3个共点力的作用,其中一个力为恒力,两个变力方向的夹角不变.

解题策略:对物体进行受力分析,根据两变力方向夹角不变的特点和圆的固定弦对应圆周角不变的性质,画出力的矢量三角形及其外接圆;确定矢量三角形在辅助圆内的变化范围,由动态矢量三角形的变化确定力的变化情况.

图5

例3.如图5所示,置于地面的矩形框架中用两细绳拴住质量为m的小球,绳OB水平.设绳OA、OB对球的拉力大小分别为F1和F2,他们的合力为F.现将框架在竖直平面内绕左下端缓慢旋转90°,在此过程中

(A)F1先增加后减小.

(B)F2先增加后减小.

(C)F先增加后减小.

(D)F先减小后增加.

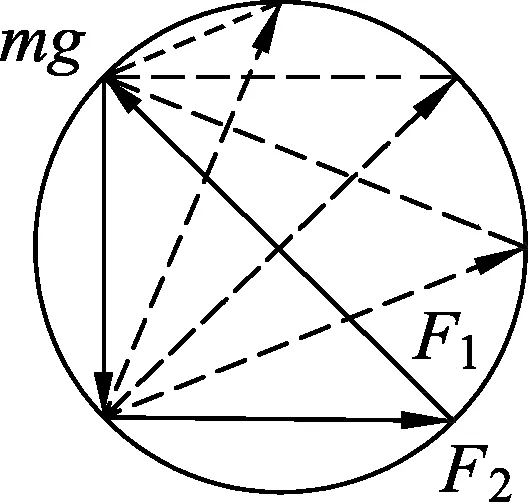
图6

解析:如图6所示,绳子拉力发生变化,但二者夹角不变,小球受到力的矢量三角形的外接辅助圆固定,此时F2方向垂直于mg方向.在矩形框旋转的过程中,F2逐渐从水平到竖直,根据圆的特性可知F2先增加后减小,F1一直减小,二者合力大小不变,所以选(B).

1.4 矢量图解法评析

矢量图解是求解共点力动态平衡问题中最常见的方法,主要考查了学生对于受力平衡、动态变化的理解和基本模型建构的能力,对于科学思维的要求不高,属于科学思维水平划分的5个水平等级中的水平2——“能在熟悉的问题情境中应用常见的物理模型;能对比较简单的物理现象进行分析和推理.”[3]3种图解法的适用条件和对应的题型不同,其中极限法要求力的大小单调变化,而通常情况下往往需要判断之后才能确定变化规律,因此一般不建议采用极限法.

2 解析法

适用条件:物体受到3个共点力的作用,其中一个力为恒力,有两个力方向的夹角不变,即恒力和其中一个变力之间或两变力之间的夹角不变.

解题策略:对物体某一状态进行受力分析,建立平衡状态方程组,联立求解得到自变量与因变量之间的函数关系式,根据自变量的变化确定因变量的变化情况;常见的解析法主要有正交分解、正弦定理和拉密定理.

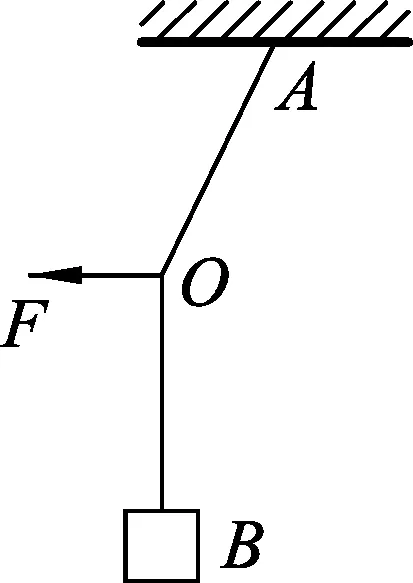
图7

例4.如图7所示,质量为m的物体用轻绳AB悬挂于天花板上.用水平向左的力F缓慢拉动绳的中点O,用T表示绳OA段拉力的大小,在O点向左移动的过程中

(A)F逐渐变大,T逐渐变大.

(B)F逐渐变大,T逐渐变小.

(C)F逐渐变小,T逐渐变大.

(D)F逐渐变小,T逐渐变小.

2.1 正交分解

图8

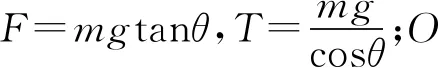
2.2 正弦定理

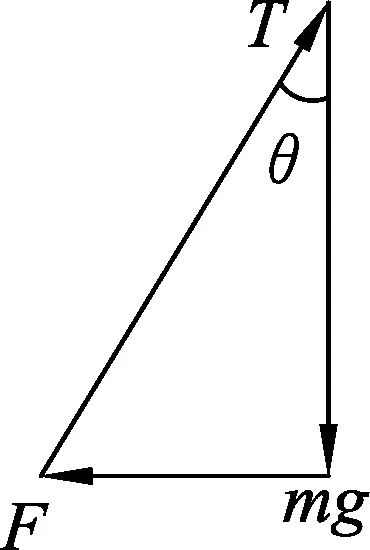
图9

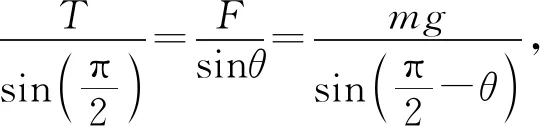
2.3 拉密定理

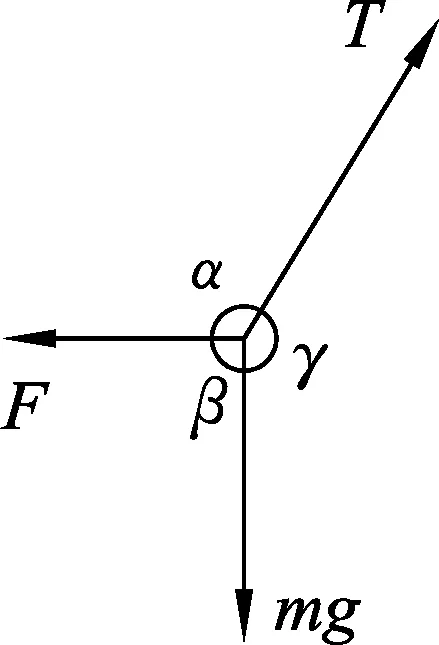
图10

2.4 解析法评析

解析法是共点力动态平衡问题中的另一类常见解法,主要考查了学生受力分析、模型建构和数学运算的能力,对科学思维要求进一步提升,此类题对应科学思维水平等级3——“能在熟悉的问题情景中根据需要选择恰当的模型解决简单的物理问题.”[3]正交分解是高考中最常见的解析法,正弦定理和拉密定理通常出现在自主招生和竞赛中;一般情况下,三者是通用的,但在求解某些问题中正弦定理和拉密定理可以极大地简化计算,同时可以拓展学生解题思路,有效提高思维品质.

3 数形结合法

当3个共点力组成动态平衡问题不能通过单一的矢量图解法或者解析法求解时,则考虑将上述两类方法进行有机组合,先图解分析再进行解析运算;常见的数形结合法主要有相似三角形法和角度对称法.

3.1 相似三角形法

适用条件:物体受到3个共点力的作用,其中一个力为恒力,一个变力的方向始终指向空间某一个固定的点,即存在一个变力为有心力.

解题策略:对物体进行受力分析并画出力的矢量三角形,寻找与力的矢量三角形相似的空间几何三角形,根据相似关系通过几何三角形边长和角度变化确定力的变化情况.

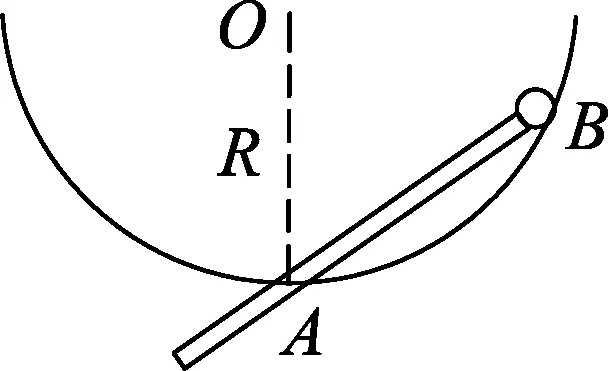
图11

例5.如图11所示,在圆心为O半径为R的光滑半球碗的底部A开一个小孔,碗内有一质量为m体积可忽略的光滑小球,现用一细杆穿过A孔,缓慢将小球从碗底推至与碗水平的位置,求整个运动过程中杆对球的支持力F和碗对球的支持力N大小变化情况.

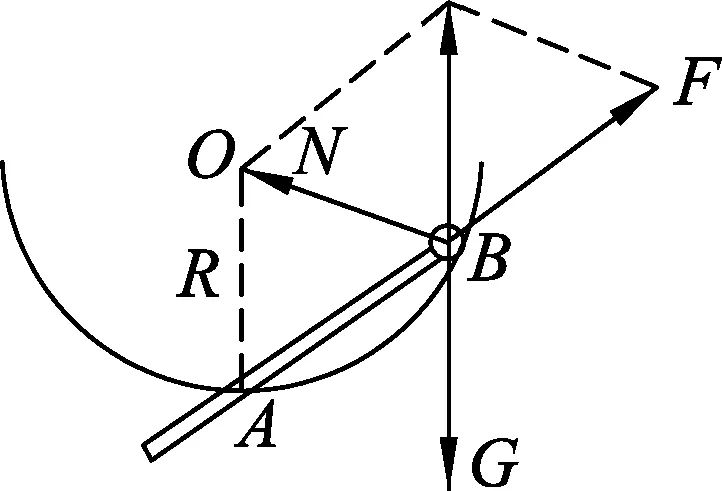
图12

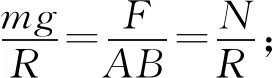
3.2 角度对称法

适用条件:轻绳上挂有可自由滑动的挂钩或滑轮.

解题策略:轻绳上可自由滑动的挂钩或滑轮,由于轻绳上拉力处处相等,只有当两侧轻绳关于挂钩或滑轮所受的第三个力的方向恰好对称时,系统才会平衡.

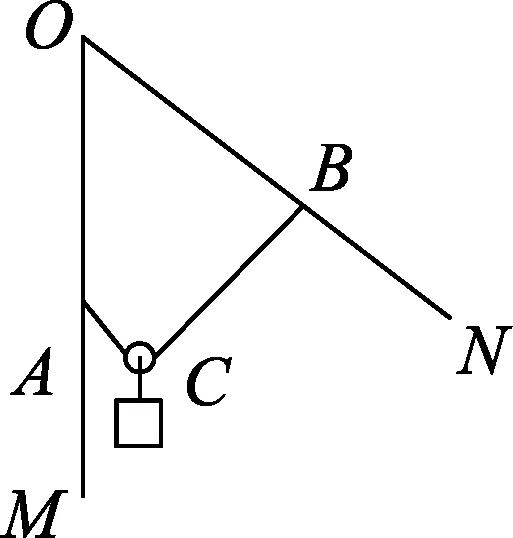
图13

例6.如图13所示,在竖直平面内,一根不可伸长的轻绳两端打结系于“V”型杆上AB两点,已知OM边竖直,且AO=BO,CB垂直于ON,细绳AB绕过光滑的滑轮,质量为m的重物悬挂于滑轮下处于静止状态.若在纸面内绕端点O按顺时针方向缓慢转动“V”,直到ON边竖直,绳子的张力为T,A点处绳子与杆之间摩擦力为fA,则

(A) 张力T一直增大.

(B) 张力T先增大后减小.

(C) 摩擦力fA一直减小.

(D) 摩擦力fA先增加后减小.

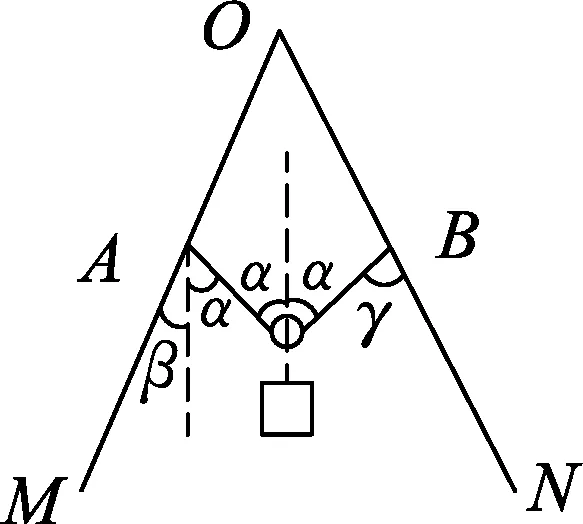
图14

3.3 数形结合法评析

数形结合法需要学生具备创造性见解的能力和品质,集中体现了学生的分析推理和科学论证能力,对应科学思维水平划分中的水平4——“能将实际问题中的对象和过程转换成物理模型;能对综合性物理问题进行分析和推理.”[3]在物理教学中结合数学知识求解,是实践STEAM理念的重要举措,有助于促进学科融合和发散思维的培养,从而有效发展学生的科学素养.