钢筋混凝土框架结构整体延性与层间延性关系

胡利烽

摘 要：采用理论分析的方法，在假定的理想结构侧移状态下，推导出框架结构整体位移延性与层间位移延性的关系，在进行结构设计时，可为设计者提供相关参考：低位置的层间延性相比于高位置的层间延性，对结构整体延性的影响较大。

关键词：框架结构;整体延性;层间延性;理论解析

中图分类号：TU375.4            文献标识码：A            文章编号：1006—7973（2019）04-0056-04

1 引言

结构的延性能力反映了结构在地震作用进入塑性阶段的变形和耗能能力，而钢筋混凝土框架结构作为最普遍的结构形式，各国学者对其延性做了大量研究。常用的结构延性指标分为结构整体延性系数和局部延性系数两大类，而把握结构局部延性和整体延性能力的协调匹配关系，将对结构以延性为目的性能设计提供参考途径。

对于结构的整体延性和局部延性能力的需求关系，我国规范[1]明确提出混凝土结构设计要在以构件设计的基础上扩展到针对于结构整体的设计，但没有明确的描述其局部延性与整体延性间的关系。欧洲的规范[2]给出了关于混凝土构件的曲率延性系数和整体延性系数之间的关系。Kunnath等[3]研究了框架结构杆件延性和系统延性的关系，指出结构局部延性应大于结构整体延性，即构件延性大于层间延性大于结构整体延性。Biondini[4]等通过分析多层混凝土框架结构整体延性与柱延性关系，发现局部延性与结构整体延性之间的关系依赖于结构的侧向倒塌机制。孙克俭[5]通过共扼梁法计算结构的侧移，推导了等高排架和典型规则框架结构的位移延性计算公式，指出结构整体位移与结构层次和构件有关。周靖[6]对5层与10层的两个混凝土框架结构，进行了8条地震波作用下的弹塑性时程分析，统计分析得出结构整体延性与柱曲率延性之间的关系。蔡健等[7]通过对国内多个钢筋混凝土框架柱和框架试验数据的整理，考虑了多因素的影响，回归分析得出一个延性系数的经验公式，以此来表示柱与结构整体位移延性关系。

2 框架结构整体位移变形

2.1框架结构整体剪切变形

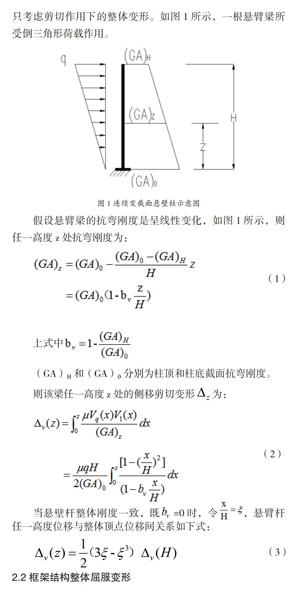
从宏观控制分析的角度看，我们可以把实际的建筑结构整体模拟成一根“竖向悬臂梁”，其所受的水平风荷载和地震作用可以看作倒三角形荷载作用于这跟悬臂梁上。当框架结构层数不高时，框架结构的侧移主要表现为剪切变形[8]，且表现的主要破坏形式为剪切破坏。本文只讨论层数不多的多层框架结构，所以在把框架结构等效为“竖向悬臂梁”时只考虑剪切作用下的整体变形。如图1所示，一根悬臂梁所受倒三角形荷载作用。

假设悬臂梁的抗弯刚度是呈线性变化，如图1所示，则任一高度z处抗弯刚度为：

上式中

（GA）H和（GA）0分别为柱顶和柱底截面抗弯刚度。

则该梁任一高度z处的侧移剪切变形为：

當悬壁杆整体刚度一致，既=0时，令，悬臂杆任一高度位移与整体顶点位移间关系如下式：

2.2 框架结构整体屈服变形

由于构件在屈服前各截面处于弯矩—曲率图的线性阶段，所以此时曲率的分布应遵循弯矩的分布情况。而各层柱所受侧向荷载大小不同和截面不同，将导致各层柱的曲率分布情况也不相同，假设框架结构每层的层高相同，则结构第r层相对于地面的侧向位移为[9]：

其中为结构屈服时第i层柱子底部的曲率大小，为层间柱高，为第i层柱子的反弯点位置。

现假设框架柱各截面屈服曲率一样，即：;框架结构底层框架柱的反弯点出现在柱高的2/3处，其余各层柱的反弯点出现在柱中部，即，，代入式（10）可得框架结构顶点屈服位移：

3 框架结构整体与层间位移延性关系解析

框架结构整体虽然呈现一种剪切变形，而在层间主要表现为层间的弯曲变形[8]，即层间框架柱的弯曲变形。为了使结构具有更好的抗震性能，在设计时往往把结构设计成强柱弱梁，使结构中的柱在在结构构件中最后形成塑性铰而破坏，形成梁铰侧移机构的破坏形式，图2为一种理想的梁铰侧移机构。

其中，图2只画出了结构的塑性变形，在各个框架柱屈服前，其框架梁的临界截面率先达到屈服并发展成塑性铰，而随着地震作用的进行，在结构底层的柱的柱根形成塑性铰，导致结构整体失去抗侧移的能力，形成倒塌，而此时结构的整体位移与柱塑性铰关系如下：

式中：代表结构的极限位移，代表结构的屈服位移。为柱的极限塑性转铰，可以用柱的极限曲率表示为

其中：为框架柱极限曲率，为框架柱的屈服曲率，为框架柱的塑性铰区长度。

结合式（3）、（6）、（7）可得

根据式（5）、（8）可得某层相对于地面的屈服位移和极限位移分别为：

上式中;其中z代表某一层的层数，r代表结构总层数，。

从式（9）和式（10）可得某一层相对于下一层的层间屈服位移和极限位移分别为：

从式（11）中可以看出层间屈服位移与楼层所在位置无关，这是因为除了一层外假设了所有框架柱屈服曲率和反弯点得高度一致，因此除一层外得到的其它层间屈服位移也一致。结合式（11）、（12），可得层间位移延性系数与框架柱曲率延性系数的一个关系式：

根据式（4）、（5）、（7）可得框架结构整体位移延性系数与框架柱曲率延性系数关系式：

根据式（13）、（14）可得到框架结构层间位移延性系数与整体位移延性系数间关系：

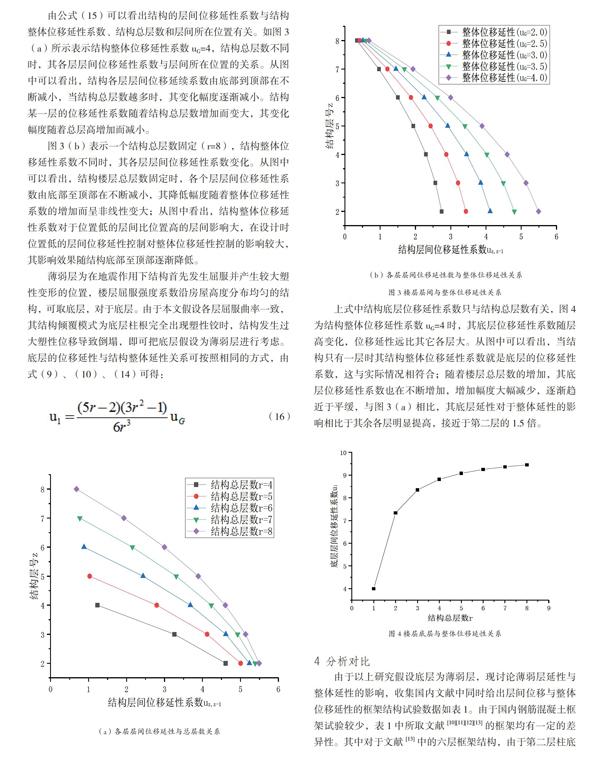
由公式（15）可以看出结构的层间位移延性系数与结构整体位移延性系数、结构总层数和层间所在位置有关。如图3（a）所示表示结构整体位移延性系数uG=4，结构总层数不同时，其各层层间位移延性系数与层间所在位置的关系。从图中可以看出，结构各层层间位移延续系数由底部到顶部在不断减小，当结构总层数越多时，其变化幅度逐渐减小。结构某一层的位移延性系数随着结构总层数增加而变大，其变化幅度随着总层高增加而减小。

图3（b）表示一个结构总层数固定（r=8），结构整体位移延性系数不同时，其各层层间位移延性系数变化。从图中可以看出，结构楼层总层数固定时，各个层层间位移延性系数由底部至顶部在不断减小，其降低幅度随着整体位移延性系数的增加而呈非线性变大;从图中看出，结构整体位移延性系数对于位置低的层间比位置高的层间影响大，在设计时位置低的层间位移延性控制对整体位移延性控制的影响较大，其影响效果随结构底部至顶部逐渐降低。

薄弱层为在地震作用下结构首先发生屈服并产生较大塑性变形的位置，楼层屈服强度系数沿房屋高度分布均匀的结构，可取底层，对于底层。由于本文假设各层屈服曲率一致，其结构倾覆模式为底层柱根完全出现塑性铰时，结构发生过大塑性位移导致倒塌，即可把底层假设为薄弱层进行考虑。底层的位移延性与结构整体延性关系可按照相同的方式，由式（9）、（10）、（14）可得：

（a）各层层间位移延性與总层数关系

（b）各层层间位移延性数与整体位移延性关系

上式中结构底层位移延性系数只与结构总层数有关，图4为结构整体位移延性系数uG=4时，其底层位移延性系数随层高变化，位移延性远比其它各层大。从图中可以看出，当结构只有一层时其结构整体位移延性系数就是底层的位移延性系数，这与实际情况相符合;随着楼层总层数的增加，其底层位移延性系数也在不断增加，增加幅度大幅减少，逐渐趋近于平缓，与图3（a）相比，其底层延性对于整体延性的影响相比于其余各层明显提高，接近于第二层的1.5倍。

4 分析对比

由于以上研究假设底层为薄弱层，现讨论薄弱层延性与整体延性的影响，收集国内文献中同时给出层间位移与整体位移延性的框架结构试验数据如表1。由于国内钢筋混凝土框架试验较少，表1中所取文献[10][11][12][13]的框架均有一定的差异性。其中对于文献[13]中的六层框架结构，由于第二层柱底部率先于第一层柱底部形成塑性铰，导致结构底层并未屈服，结构因为第二层的破坏而失去承载能力，所以可以视第二层形成薄弱层，因此取第二层的位移延性来比较。

根据表1可见其公式计算比值高于试验比值，是因为本公式是基于一种理想的假设模型下推导，忽略了部分因素对其位移延性的影响，如层间高度的变化，柱截面的变化。以及底层柱所受轴压等因素，均会对框架结构的整体与层间延性位移产生影响。因此其计算时可以乘以一个或多个折减系数，这一个或多个折减系数与其柱梁截面面积、跨度、层高等变化有关，这些系数的取值与相互关系有待更进一步的研究与确定。

把公式计算的延性比随楼层变化的曲线与试验得到的延性比随楼层变化的曲线重合比较（即公式（16）乘以一个比值α），如图5，其试验数据和公式计算的底层与整体的位移延性比都随结构层数的增高而提高，由于理论模型的理想性和试验的不确定性，导致提高幅度略有差异。

5 结语

在多层框架结构体系中，层间位移的延性与所在层间位置有关，由底部至顶部呈逐渐降低趋势。越低的层间位置的位移延性越高，一般高于整体位移延性，越高的层间位置的位移延性越低，一般低于整体位移延性。

在钢筋混凝土多层框架结构中，当结构总层数确定时，随着结构整体位移延性的增加，各个层层间位移延性系数由底部至顶部在不断减小，其降低幅度随着整体位移延性系数的增加而变大。

在假设底层为薄弱层的情况下，其底层位移延性相比于其余各层明显增加，接近于第二层的1.5倍，且底层延性随结构总层数增加而增加，增加幅度逐渐减小。

根据结构整体延性与层间延性关系变化，可为设计者提供相关参考：位置低的层间位移延性对整体位移延性的影响较大，其影响效果随结构底部至顶部逐渐降低。

参考文献：

[1] 中华人民共和国住房和城乡建设部.GB

50010-2010混凝土结构设计规范[S].北京;中国建筑工业出版社.2010.

[2] CEN/TC250. EN 1998-1 Eurocode 8：design of structures for earthquake resistantance. Part 1：general rules. seismic actions and rules for buildings[S]. Brussels：European Committee for Standardization.2004.

[3] Kunnath S K，Kalkan E.Evaluation of seismic deformation demands using non-Linear procedures in multistory steel and concrete moment frames[J].ISET Jou-Nal of Earthquake Technology，2004，41（1）：159-181.

[4] Biondini F，Toniolo G.Seismic behaviors of concrete frame：expri- amental and analytical verification of Eurocode 8 design rules [C]//Fib Symposium on concrete Structures in Seismic Regions.Athens：International Federation for Structural Concrete，2003：1-12.

[5] 孙克俭.框架结构侧移的近似计算[J].工程力学，1990.7（4）：50-53.

[6] Zhou J，He F，Liu T.Curvature ductility of columns and structural displacement ducyility in RC frame structures subjected to ground motions[J].Soil Dynamics&Earthquake Engineering，2014，63（1）：174-183.

[7] 蔡健，周靖，方小舟.钢筋混凝土框架抗震位移延性系数研究[J].工程抗震与加固改造，2005，27（3）：2-6.

[8] 梁兴文，史庆轩.混凝土结构设计{M}.北京：科学出版社，2004.

[9] Park，T.Pauly.Reinforced Concrete Structures[M].John Wiley&Sons，Inc，1975：103-105.

[10] 薛伟辰，程斌，李杰.双层双跨高性能混凝土框架抗震性能研究[J].土木工程学报，2004，37（3）：58-65.

[11] 田承昊.异形柱框架抗震性能试验研究及其有限元分析[D].天津：天津大学，2005.

[12] 薛伟辰，胡翔.四层两跨高性能混凝土框架抗震性[J].建筑结构报，2007，28（5）：69-79.

[13] 薛伟辰，杨新磊，王蕴，窦祖融.六层两跨现浇柱预制梁框架抗震性能试验研究[J].建筑结构学报，2008，29（6）：25-32.