非稳态窜流多段压裂水平井井底压力分析
2019-10-08姜瑞忠刘秀伟崔永正张春光郜益华
姜瑞忠,刘秀伟,崔永正,张春光,郜益华,潘 红,王 星
(1.中国石油大学(华东)石油工程学院,山东青岛266580;2.中海油研究总院有限责任公司,北京100028;3.中国石油大港油田分公司采油工艺研究院,天津300280)
北美致密油的成功开采以及当今日益紧张的能源形势,使得非常规石油资源成为行业的热点[1-4]。由于致密油储层具有渗透率低、孔喉细小、流动条件差等特性[5-6],导致常规水平井技术开发效果不理想;而多段压裂水平井技术通过对水平井进行多段压裂形成多条裂缝通道,再加上水平井横向贯穿油层,能够大大提高油井产能,从而使得多段压裂水平井技术广泛应用于提高致密油产量[7]。对于多段压裂水平井的渗流规律,中外诸多学者对其进行了研究,其中使用最广泛的就是线性流模型。
BROWN等在2009年提出了三线性流模型研究多段压裂水平井的井底压力[8],压力和压力导数在流动后期与MEDEIROS等提出的半解析解[9]拟合较好,验证了其模型的正确性;之后,姚军等在OZKAN模型基础上,建立了考虑启动压力梯度的三线性流模型,并研究启动压力梯度等因素的影响[10],其压裂改造区采用Warrant-Root拟稳态窜流模型[11]。
2012年,STALGOROVA等建立五线性流多段压裂水平井模型与数值模型结果进行对比,验证了其模型的合理性[12];之后,姬靖皓等建立了考虑启动压力梯度和应力敏感的五线性流模型[13],其压裂改造区同样采用了Warrant-Root拟稳态窜流模型,绘制了相应的井底压力动态曲线;WU等采用等效渗透率将压裂改造区看作单重介质,同时综合考虑启动压力梯度和应力敏感建立了五线性流模型[14]。
但是由于致密油储层基岩孔喉为纳米级孔道,且渗透率极低,因此基岩中的非稳态窜流不能忽略[15],应用Warrant-Root拟稳态窜流模型或者利用等效渗透率的方法所得到的解精确度不高。为此,笔者基于STALGOROVA五线性流模型,建立了同时存在启动压力梯度和应力敏感且考虑了压裂改造区之中非稳态窜流的不稳定渗流数学模型,并对其进行求解、绘制井底压力动态曲线。
1 物理模型
在对水平井实施多段压裂改造过程中,主裂缝周围多条天然裂缝会被连通从而形成复杂的缝网,但较远的储层并未受到压裂改造的影响,仍为致密储层(图1a)。依据其主裂缝和压裂改造区的分布特点,可简化得到其等效的流动模型(图1b)。由对称性可知,只需研究每条主裂缝控制区域的四分之一区域流动即可。将主裂缝控制区域的四分之一区域划分为5个区域(图2),区域1,2,3为未改造区域,看作单重介质;区域4为压裂改造区域,看作是双重介质,采用DE SWAAN模型[16](图3);区域5为主裂缝区域。在区域1,2,3内考虑启动压力梯度的影响,区域4,5考虑应力敏感的影响。
物理模型基本假设为:①油藏的外边界为封闭边界。②水平井位于油藏中心处且以定产量生产。③油藏中流体由未改造区流向改造区,再由改造区流向主裂缝,最后流向水平井。④地层岩石和流体微可压缩,流动过程温度不变,忽略重力、毛管压力以及井筒阻力的影响。

图1 多段压裂水平井物理模型Fig.1 Physical model for multistage fractured horizontal well

图2 主裂缝控制区域的四分之一区域流动方向示意Fig.2 Schematic of flow directions in a quarter area controlled by main fractures

图3 裂缝与基质系统示意Fig.3 Schematic of fracture and matrix system
2 数学模型及求解
为方便推导与求解,定义无因次变量见表1。

表1 数学模型所包含的无因次变量Table1 Dimensionless variables contained in mathematical model
2.1 数学模型
2.1.1 区域1
考虑启动压力梯度时区域1的渗流控制方程为:

结合边界条件,对(1)式进行无因次化得到区域1无因次数学模型为:
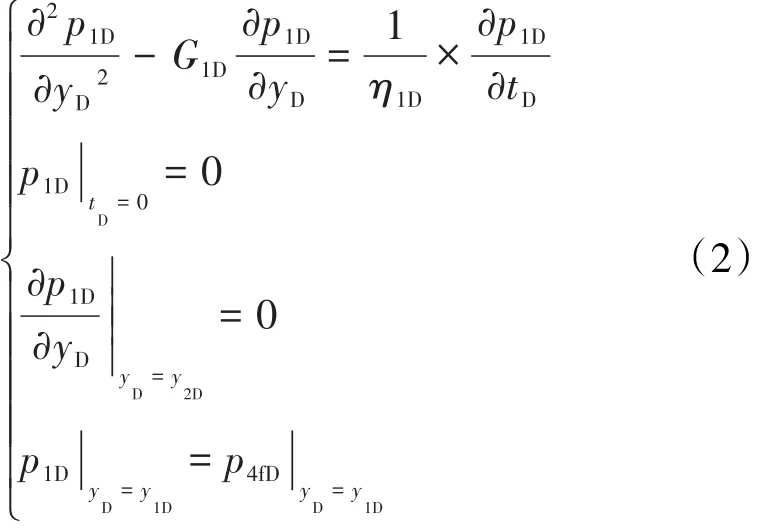
2.1.2 区域2
区域2与区域1同理可以得到考虑启动压力梯度时区域2的无因次数学模型为:

2.1.3 区域3
由于区域2向区域3存在流体补充,可以将该流体补充项表示为:

从而推导得到区域3的渗流控制方程为:

结合边界条件,对(5)式进行无因次化得到区域3无因次数学模型为:

2.1.4 区域4
2.1.4.1 基质系统
区域4基质的渗流控制方程为:

结合边界条件,对(7)式无因次化后得到区域4基质系统无因次数学模型为:

2.1.4.2 裂缝系统
区域4裂缝系统考虑到应力敏感效应,采用渗透率模量来表示裂缝渗透率为:

同时,考虑到区域1向区域3的流体补充项以及基质与裂缝间的窜流项:

可以推导得到区域4裂缝系统的渗流控制方程为:

结合边界条件,将(12)式无因次化后得到区域4裂缝系统无因次数学模型为:

2.1.5 区域5
和区域4裂缝系统相同,区域5同样考虑到应力敏感效应,渗透率受到压力影响,采用渗透率模量来表示主裂缝渗透率为:

考虑到区域4向区域5的流体补充项:

可以推导得到区域5的渗流控制方程为:
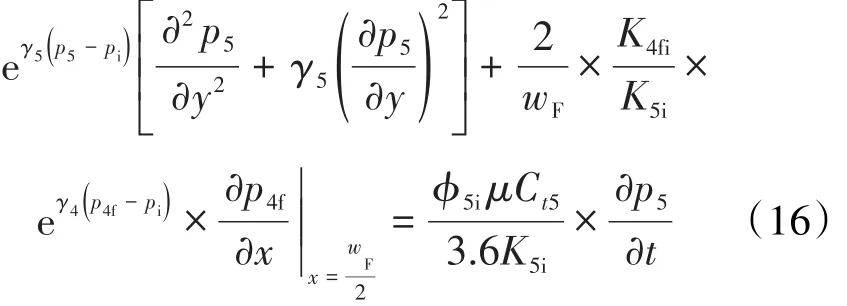
结合边界条件,将(16)式进行无因次化后可得到区域5无因次数学模型为:

2.2 数学模型求解
2.2.1 区域1
将区域1无因次数学模型进行Laplace变化,得:

对(18)式偏微分方程进行求解可得:

其中:
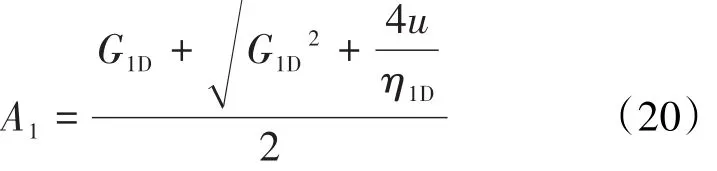

由于区域4的流动与x方向无关,故(19)式又可写为:

2.2.2 区域2
同理区域1求解方法,可以得到区域2的解为:

其中:

2.2.3 区域3
同理将区域3无因次数学模型进行Laplace变化,可得:

由区域2压力解可得:

其中:
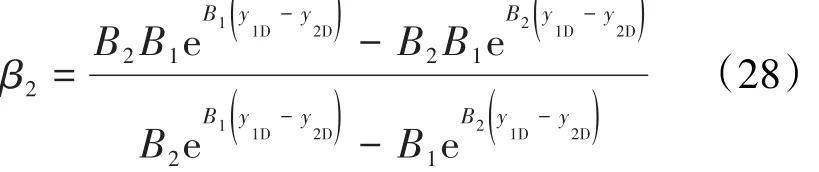
将(27)式代入(26)式中得:

其中:

对(29)式进行求解得区域3压力解为:

其中:

2.2.4 区域4
2.2.4.1 基质系统
将区域4基质系统无因次数学模型进行La⁃place变化可得:

对(34)式求解可得:

其中:

2.2.4.2 裂缝系统
由于(13)式中无因次渗透率模量的存在,使得该数学模型具有很强的非线性,为了便于求解,此利用Pedrosa[17]变化以及摄动变化式消除非线性,其计算式为:
由于γ4D为小量,所以零阶摄动解τ40可以看作是近似解且具有足够的精度要求,故对区域4裂缝系统数学模型进行Pedrosa变化以及摄动变化,然后进行Laplace变化得:

由区域1压力解可得:

其中:

由区域4基质系统压力解可得:

其中:

由区域3压力解可得:

其中:

将(41)式、(43)式和(45)式代入(40)式中可得:

其中:
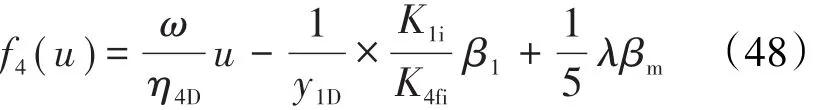
对(47)式进行求解得到:
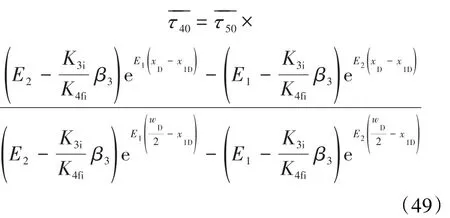
其中:

2.2.5 区域5
区域5主裂缝数学模型求解与区域4裂缝系统数学模型求解相同,利用Pedrosa变化以及摄动变化消除非线性,然后进行Laplace变化可得:
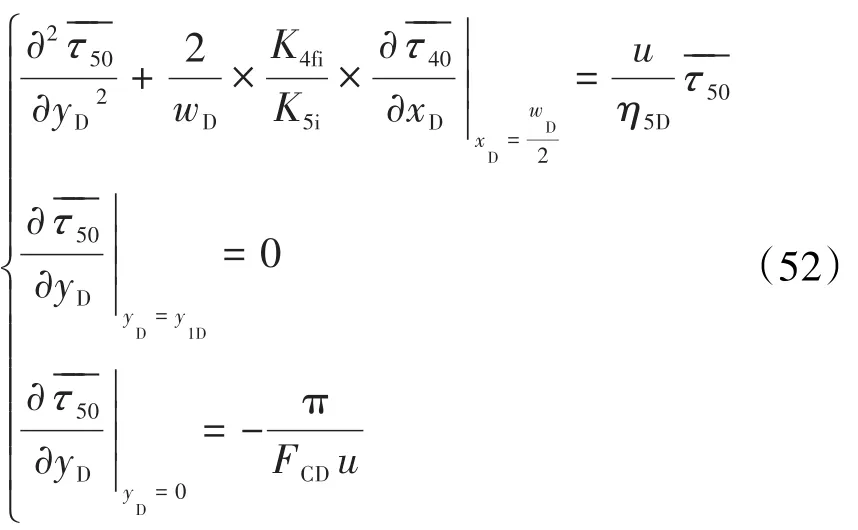
由区域4压力解得:

其中:

将(53)式代入(52)式可得:

其中:

对(55)式进行求解可得:

当yD=0时,主裂缝压力解即为Laplace空间下无因次井底压力解为:

同时采用Duhamel原理引入无因次井筒储集系数和表皮系数,得到考虑井筒储集效应和表皮效应的井底压力解为:

对(59)式进行Stehfest数值反演[18],然后进行摄动反变化,便可得到真实空间下的井底压力解为:

3 井底压力曲线形态分析
依据前面推导出的真实空间下的无因次井底压力解,在双对数坐标系下绘制无因次井底压力曲线和无因次井底压力导数曲线,据此来描述渗流过程。
3.1 流动形态划分
由双对数坐标系下的无因次井底压力和无因次井底压力导数曲线(图4)可见,流动形态可以划分为6个阶段:①早期井筒储集效应阶段,无因次井底压力和无因次井底压力导数曲线重合且逐渐上升。②表皮效应阶段,井筒储集效应减弱,无因次井底压力和无因次井底压力导数曲线开始分离,且无因次井底压力导数曲线达到一定值后开始下降,形成明显的驼峰,而无因次井底压力曲线则继续上升。③压裂改造区基质与裂缝的非稳态窜流阶段,无因次井底压力导数曲线呈现出一个“凹子”形状,无因次井底压力曲线继续上升。④整个压裂改造区的线性流阶段,无因次井底压力和无因次井底压力导数曲线上升。⑤压裂改造区和未改造区的线性流阶段,无因次井底压力和无因次井底压力导数曲线继续上升并且逐渐接近。⑥受边界影响的流动阶段,无因次井底压力和无因次井底压力导数曲线最终再次重合,且继续上升。

图4 多段压裂水平井井底压力动态曲线Fig.4 Dynamic curve of bottomhole pressure in multistage fractured horizontal well
3.2 模型验证与对比
松辽盆地致密油藏X区块某井在实施多段压裂增产措施一段时间后进行了压力恢复试井测试,现场实测数据为时间-压力关系,进行模型验证时,将实测数据进行无因次化,然后绘制实测数据的双对数压力特征曲线,并与所建立的五线性流压力特征曲线进行对比。从图5可以看到,早期井筒储集效应阶段的数据点并未测出,但是中间区域的数据点与五线性流压力特征曲线拟合较好,呈现出较为明显的2个线性流阶段,且具有窜流的“凹子”特征,从而验证了所建模型的合理性。

图5 模型验证与对比Fig.5 Model verification and comparison
从图5也可以看到,与考虑拟稳态窜流的试井曲线相对比,在前期和后期两者曲线基本一致。而在窜流阶段,非稳态窜流无因次井底压力导数曲线上的窜流“凹子”要比拟稳态的浅且宽。其原因为在所取的计算参数相同时,非稳态窜流条件下基质系统中的流体对系统压力改变的响应要比拟稳态条件下更敏感[19],因此不会像拟稳态一样出现很明显的“凹子”段,且无因次井底压力和无因次井底压力导数曲线上对于窜流阶段的反映会更早。
3.3 参数敏感性分析
3.3.1 窜流系数
从图6可以看出,随着窜流系数的增加,无因次井底压力曲线逐渐下移,无因次井底压力导数曲线上非稳态窜流的“凹子”相应前移,窜流发生的时间变早。其原因为,窜流系数越大,表明基质系统渗透率与裂缝系统渗透率差别越小,基质与裂缝之间的窜流在较小的压差下就可以发生,裂缝中的压力达到基质向裂缝窜流的压力条件所需时间较短,进而“凹子”前移,窜流发生变早。

图6 窜流系数对压力动态曲线的影响Fig.6 Effect of crossflow coefficient on dynamic pressure curve
3.3.2 弹性储容比
从图7可以看出,随着弹性储容比的减小,无因次井底压力导数曲线的非稳态窜流“凹子”略变宽变深,并没有拟稳态窜流时变化那么明显。其原因为,弹性储容比越小,裂缝储集的流体越少,裂缝供液能力弱,开井生产短时间内裂缝系统会产生较大压降,而基质系统向裂缝系统的流体补充需要较长时间才可以使得裂缝系统压力提升,从而使得“凹子”略变宽变深。
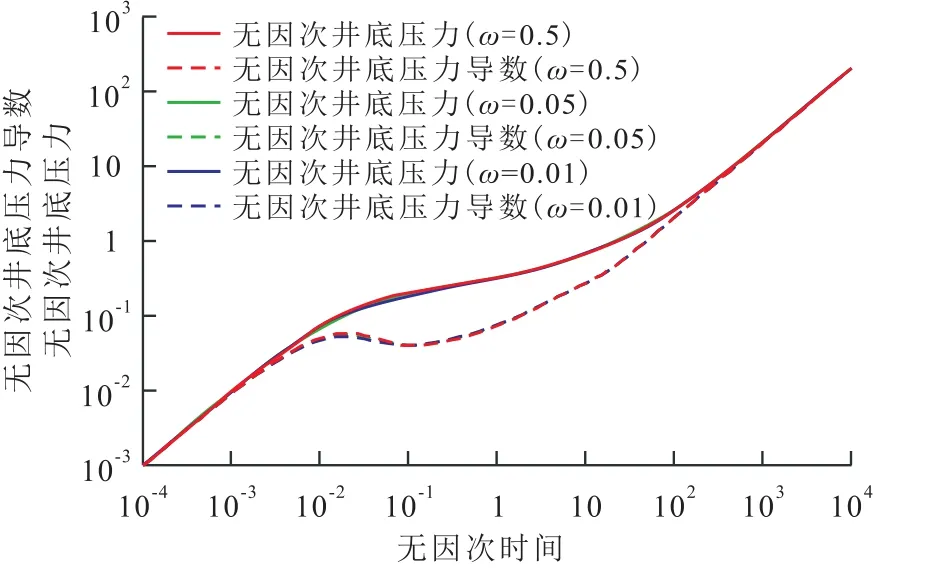
图7 弹性储容比对压力动态曲线的影响Fig.7 Effect of elastic storativity ratio on dynamic pressure curve
3.3.3 主裂缝渗透率模量
从图8可以看出,随主裂缝无因次渗透率模量的增加,无因次井底压力和无因次井底压力导数曲线主要在边界控制流阶段发生变化,无因次井底压力和无因次井底压力导数曲线随之上翘。其原因为,在流动阶段初期,整个生产过程中压降相对较小,地层压力变化较小,此时主裂缝渗透率受压力的影响较小,应力敏感性弱,但一段时间后,地层压力变化较大,主裂缝渗透率应力敏感性增强,且无因次渗透率模量越大,渗透率变化越大,渗流阻力越大,流体流动所需的压差越大,从而造成压力和压力导数曲线的上翘。

图8 主裂缝渗透率模量对压力动态曲线的影响Fig.8 Effect of permeability modulus of main fractures on dynamic pressure curve
3.3.4 未改造区域启动压力梯度和渗透率
从图9可以看出,未改造区域的无因次启动压力梯度取值的增加造成无因次井底压力和无因次井底压力导数曲线的上移。因无因次启动压力梯度的增加,未改造区域物性变差,流体流动阻力变大,压力消耗越大,导致无因次井底压力和无因次井底压力导数曲线下移。

图9 未改造区域启动压力梯度对压力动态曲线的影响Fig.9 Effect of threshold pressure gradient in unstimulated area on pressure dynamic curve
未改造区域渗透率的增加则会造成无因次井底压力和无因次井底压力导数曲线的下移,与无因次启动压力梯度正好相反(图10)。因渗透率的增加,未改造区域物性变好,渗流阻力减小,压力消耗较小,导致无因次井底压力和无因次井底压力导数曲线下移。

图10 未改造区域渗透率对压力动态曲线的影响Fig.10 Effect of permeability of unstimulated area on dynamic pressure curve
4 结论
为了多段压裂水平井开发提供理论依据,建立了考虑压裂改造区非稳态窜流的五线性流数学模型,通过Laplace变化、Pedrosa变化以及摄动变化等一系列数学物理方法,求出解析解。依据流动形态,将试井曲线分为6个阶段:早期井筒储集效应阶段、表皮效应阶段、压裂改造区基质与裂缝的非稳态窜流阶段、整个压裂改造区的线性流阶段、压裂改造区和未改造区的线性流阶段以及受边界影响的流动阶段。
依据数学模型的敏感性参数分析认为:窜流系数越大,非稳态窜流出现得越早;弹性储容比的减小,会造成无因次井底压力导数曲线上的“凹子”变宽变深,但并不明显;随着主裂缝无因次渗透率模量的增大,边界控制流阶段的无因次井底压力和无因次井底压力导数曲线上翘;未改造区域的无因次启动压力梯度的增加会造成未改造区域物性变差,无因次井底压力和无因次井底压力导数曲线会上移;相反,未改造区域渗透率的增加则会造成未改造区域物性变好,无因次井底压力和无因次井底压力导数曲线会下移。
符号解释
x,y——距离,m;wF——主裂缝宽度,m;x1——压裂改造区半宽,m;x2——主裂缝半间距,m;y1——裂缝半长,m;y2——油藏半宽,m;Rm——基质系统圆形球体的球向半径,m;pjD——第j区无因次压力;j——区域编号,其值为1—5;n——主裂缝数目;h——油藏厚度,m;Kref——参考渗透率,mD;Q——单条主裂缝产量,m3/d;μ——地层原油黏度,mPa·s;B——原油体积系数;p——压力,MPa;i——初始值;xD,yD——无因次距离;Lref——参考长度,m;x1D——无因次压裂改造区半宽;y1D——无因次裂缝半长;x2D——无因次主裂缝半间距;y2D——无因次油藏半宽;RmD——基质系统圆形球体的无因次球向半径;R1——基质系统圆形球体颗粒半径,m;wD——无因次主裂缝宽度;tD——无因次时间;ηref——参考导压系数,μm2/(mPa·s·MPa-1);t——时间,h;ϕref——参考孔隙度;Ctref——参考综合压缩系数,MPa-1;ηjD——第j区无因次导压系数;ηj——第j区导压系数,μm2/(mPa·s·MPa-1);GjD——第j区无因次启动压力梯度;Clj——第j区流体压缩系数,MPa-1;Gj——第j区启动压力梯度,MPa/m;γjD——第j区无因次渗透率模量;γj——第j区渗透率模量,MPa-1;λ——窜流系数;K4mi——区域4基质系统初始渗透率,mD;K4fi——区域4裂缝系统初始渗透率,mD;ω——弹性储容比;ϕ4fi——区域4裂缝系统初始孔隙度;Ct4f——区域4裂缝系统综合压缩系数,MPa-1;ϕ4mi——区域4基质系统初始孔隙度;Ct4m——区域4基质系统综合压缩系数,MPa-1;FCD——裂缝导流能力;K5i——区域5初始渗透率,mD;p1——区域1压力,MPa;Cl1——区域1流体压缩系数,MPa-1;G1——区域1启动压力梯度,MPa/m;ϕ1i——区域1初始孔隙度;Ct1——区域1综合压缩系数,MPa-1;K1i——区域1初始渗透率,mD;p1D——区域1无因次压力;G1D——区域1无因次启动压力梯度;η1D——区域1无因次导压系数;p4fD——区域4裂缝系统无因次压力;p2D——区域2无因次压力;G2D——区域2无因次启动压力梯度;η2D——区域2无因次导压系数;p3D——区域3无因次压力;q23——区域2向区域3的流体补充项;K2i——区域2的初始渗透率,mD;p2——区域2压力,MPa;p3——区域3压力,MPa;Cl3——区域3流体压缩系数,MPa-1;G3——区域3启动压力梯度,MPa/m;ϕ3i——区域3初始孔隙度;Ct3——区域3综合压缩系数,MPa-1;K3i——区域3初始渗透率,mD;G3D——区域3无因次启动压力梯度;η3D——区域3无因次导压系数;p4m——区域4基质系统压力,MPa;p4mD——区域4基质系统无因次压力;η4D——区域4无因次导压系数;K4f——区域4裂缝系统渗透率,mD;γ4——区域4裂缝系统渗透率模量,MPa-1;pi——初始压力,MPa;p4f——区域4裂缝系统压力,MPa;q14——区域1向区域4的流体补充项;qm——区域4基质系统与裂缝系统间的窜流项;K4mi——区域4基质系统渗透率,mD;γ4D——区域4裂缝系统无因次渗透率模量;K5——区域5渗透率,mD;γ5——区域5渗透率模量,MPa-1;p5——区域5压力,MPa;q45——区域4向区域5的流体补充项;ϕ5i——区域5初始孔隙度;Ct5——区域5综合压缩系数,MPa-1;p5D——区域5无因次压力;η5D——区域5无因次导压系数;u——Laplace因子;γ4D——区域4裂缝系统无因次渗透率模量;A1,A2,B1,B2,C1,C2,D,E1,E2,β1,β2,β3,β4,βm,f3(u),f4(u),f5(u)——中间变量;τ40,τ50——摄动变化后的区域4和区域5无因次压力;pwD0——未考虑井筒储集和表皮系数的无因次井底压力;pwD——考虑井筒储集和表皮系数的无因次井底压力;S——表皮系数;CD——无因次井筒储集系数。
